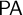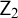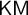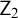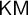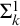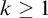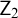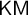1 Introduction
It is well known that set theories like
![]() $\mathsf {ZF}$
and class theories like
$\mathsf {ZF}$
and class theories like
![]() $\mathsf {GB}$
or
$\mathsf {GB}$
or
![]() $\mathsf {KM}$
are capable of interpreting many of their extensions as theories. For instance,
$\mathsf {KM}$
are capable of interpreting many of their extensions as theories. For instance,
![]() $\mathsf {ZF}$
interprets
$\mathsf {ZF}$
interprets
![]() $\mathsf {ZFC} + \mathsf {CH}$
via the constructible universe, or one may use the Boolean ultrapower construction over the notion of forcing
$\mathsf {ZFC} + \mathsf {CH}$
via the constructible universe, or one may use the Boolean ultrapower construction over the notion of forcing
![]() $\mathrm {Add}(\omega , \omega _2)$
to produce an interpretation of
$\mathrm {Add}(\omega , \omega _2)$
to produce an interpretation of
![]() $\mathsf {ZF} + \lnot \mathsf {CH}$
in
$\mathsf {ZF} + \lnot \mathsf {CH}$
in
![]() $\mathsf {ZF}$
(see [Reference Hamkins and Seabold19]). Accordingly,
$\mathsf {ZF}$
(see [Reference Hamkins and Seabold19]). Accordingly,
![]() $\mathsf {ZF} + \mathsf {CH}$
and
$\mathsf {ZF} + \mathsf {CH}$
and
![]() $\mathsf {ZF} + \lnot \mathsf {CH}$
are mutually interpretable. Mutual interpretability yields equiconsistency results, but for many set-theoretical purposes it is a coarse notion of equivalence. The issue is that we may lose information. For an example where this loss is severe, consider a model of
$\mathsf {ZF} + \lnot \mathsf {CH}$
are mutually interpretable. Mutual interpretability yields equiconsistency results, but for many set-theoretical purposes it is a coarse notion of equivalence. The issue is that we may lose information. For an example where this loss is severe, consider a model of
![]() $\mathsf {ZFC} + \neg \mathsf {CH}$
with a measurable cardinal. Carry out the constructible universe interpretation of
$\mathsf {ZFC} + \neg \mathsf {CH}$
with a measurable cardinal. Carry out the constructible universe interpretation of
![]() $\mathsf {ZF} + \mathsf {CH}$
in this model followed by the Boolean ultrapower interpretation. This produces a model of
$\mathsf {ZF} + \mathsf {CH}$
in this model followed by the Boolean ultrapower interpretation. This produces a model of
![]() $\mathsf {ZFC} + \neg \mathsf {CH}$
again, but the model cannot have a measurable cardinal. (As a forcing extension of
$\mathsf {ZFC} + \neg \mathsf {CH}$
again, but the model cannot have a measurable cardinal. (As a forcing extension of
![]() $\mathrm {L}$
, it will miss, for example,
$\mathrm {L}$
, it will miss, for example,
![]() $0^\sharp $
.) Even in less severe cases information is lost—the Boolean ultrapower interpretation produces ill-founded models, so this two-step interpretation destroys information about well-foundedness (Figure 1).
$0^\sharp $
.) Even in less severe cases information is lost—the Boolean ultrapower interpretation produces ill-founded models, so this two-step interpretation destroys information about well-foundedness (Figure 1).

Figure 1 The
![]() $\mathrm {L}$
and Boolean ultrapower interpretations.
$\mathrm {L}$
and Boolean ultrapower interpretations.
To avoid this limitation and properly establish an equivalence between theories, we need a bi-interpretation.Footnote
1
Precisely, a bi-interpretation between two theories
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are interpretations
$T_2$
are interpretations
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
, respectively, of
$\mathcal {J}$
, respectively, of
![]() $T_1$
in
$T_1$
in
![]() $T_2$
and of
$T_2$
and of
![]() $T_2$
in
$T_2$
in
![]() $T_1$
, so that there are definable functions f and g in
$T_1$
, so that there are definable functions f and g in
![]() $T_1$
and
$T_1$
and
![]() $T_2$
such that for all
$T_2$
such that for all
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
$\psi $
and
One can also view bi-interpretations on the level of individual models, saying that models
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are bi-interpretable. One should view the theory definition as a uniform version of the model definition, saying that every model of the theory
$M_2$
are bi-interpretable. One should view the theory definition as a uniform version of the model definition, saying that every model of the theory
![]() $T_1$
is bi-interpretable with a model of the theory
$T_1$
is bi-interpretable with a model of the theory
![]() $T_2$
, and vice versa, always using the same choice of interpretations.
$T_2$
, and vice versa, always using the same choice of interpretations.
Notably, theories such as PA and ZF cannot fix one model up to isomorphism, i.e., they are not categorical. We can, however, say that the second-order versions of PA and ZF are, respectively, categorical (Dedekind in [Reference Dedekind4]) and quasi-categorical (Zermelo in [Reference Zermelo43]). These categoricity results assume that second-order quantifiers indeed range over all subsets of a given domain. Thus it requires us to attribute to the mathematician a not substantiated ability to fix the meaning of second-order concepts.Footnote 2 In this context, the semantic notion of bi-interpretation can be understood as a weak form of “sameness” allowing for a weaker form of categoricity that does not rely on an arbitrary reference to the fullness of second-order quantifiers.Footnote 3 Instead of asserting that two models have isomorphic ontologies, a bi-interpretation equates the expressible ontology of possibly different models.
In pursuing this form of categoricity for set and class theories, one should examine which theories do not admit bi-interpretable models. Indeed, the interpretations of
![]() $\mathsf {ZF} + \mathsf {CH}$
and
$\mathsf {ZF} + \mathsf {CH}$
and
![]() $\mathsf {ZF} + \neg \mathsf {CH}$
given above lose information. But, are there different interpretations that do not have this problem, and instead give a bi-interpretation? As demonstrated by Enayat [Reference Enayat, Eijck, Iemhoff and Joosten6], any two bi-interpreted models of
$\mathsf {ZF} + \neg \mathsf {CH}$
given above lose information. But, are there different interpretations that do not have this problem, and instead give a bi-interpretation? As demonstrated by Enayat [Reference Enayat, Eijck, Iemhoff and Joosten6], any two bi-interpreted models of
![]() $\mathsf {ZF}$
are isomorphic. Consequently, no two different extensions of
$\mathsf {ZF}$
are isomorphic. Consequently, no two different extensions of
![]() $\mathsf {ZF}$
are bi-interpretable, and so the answer is negative. While a theory like
$\mathsf {ZF}$
are bi-interpretable, and so the answer is negative. While a theory like
![]() $\mathsf {ZF}$
has many models due to the incompleteness phenomenon, in a sense we cannot have “too many.” This property of
$\mathsf {ZF}$
has many models due to the incompleteness phenomenon, in a sense we cannot have “too many.” This property of
![]() $\mathsf {ZF}$
was first investigated by Visser in [Reference Visser39] with respect to arithmetic and later named by Enayat as tightness.Footnote
4
$\mathsf {ZF}$
was first investigated by Visser in [Reference Visser39] with respect to arithmetic and later named by Enayat as tightness.Footnote
4
Definition. A theory T is tight if every two bi-interpretable extensions of T in the same language as T have the same deductive closure.
Definition. A theory T is semantically tight if every two bi-interpretable models of T are isomorphic.Footnote 5
It is evident that every semantically tight theory is also tight.
Theorem (Enayat)
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\mathsf {KM}$
, and
$\mathsf {KM}$
, and
![]() $\mathsf {Z}_2$
are tight and semantically tight.Footnote
6
$\mathsf {Z}_2$
are tight and semantically tight.Footnote
6
A natural follow-up question is whether there are tight subsystems of these theories. This was proposed in [Reference Enayat, Eijck, Iemhoff and Joosten6, p. 14] and partially addressed with respect to
![]() $\mathsf {ZF}$
by Freire and Hamkins in [Reference Freire and Hamkins13]. They show that there are bi-interpretable models of
$\mathsf {ZF}$
by Freire and Hamkins in [Reference Freire and Hamkins13]. They show that there are bi-interpretable models of
![]() $\mathsf {Z}$
and
$\mathsf {Z}$
and
![]() $\mathsf {ZFC}^-$
.Footnote
7
Moreover, since these model constructions were uniformly produced, they obtained different bi-interpretable extensions of
$\mathsf {ZFC}^-$
.Footnote
7
Moreover, since these model constructions were uniformly produced, they obtained different bi-interpretable extensions of
![]() $\mathsf {Z}$
and
$\mathsf {Z}$
and
![]() $\mathsf {ZFC}^-$
. A full answer to this question amounts to a profound characterization of
$\mathsf {ZFC}^-$
. A full answer to this question amounts to a profound characterization of
![]() $\mathsf {ZF}$
and it should be done by obtaining bi-interpretable models of the theory
$\mathsf {ZF}$
and it should be done by obtaining bi-interpretable models of the theory
![]() $\mathsf {Z}$
with fragments of the axiom scheme of replacement.
$\mathsf {Z}$
with fragments of the axiom scheme of replacement.
In a similar light, this article investigates tightness for subsystems of
![]() $\mathsf {KM}$
, obtained by restricting the Comprehension axiom. The weakest subsystem in this hierarchy is Gödel–Bernays class theory
$\mathsf {KM}$
, obtained by restricting the Comprehension axiom. The weakest subsystem in this hierarchy is Gödel–Bernays class theory
![]() $\mathsf {GB}$
, where Comprehension is only allowed for first-order formulae. Strengthening upward adding Comprehension for
$\mathsf {GB}$
, where Comprehension is only allowed for first-order formulae. Strengthening upward adding Comprehension for
![]() $\Sigma ^1_k$
formulae gives theories we will call
$\Sigma ^1_k$
formulae gives theories we will call
![]() $\mathsf {KM}_k$
.
$\mathsf {KM}_k$
.
Our first main results are that
![]() $\mathsf {GB}$
and
$\mathsf {GB}$
and
![]() $\mathsf {KM}_k$
are not semantically tight.
$\mathsf {KM}_k$
are not semantically tight.
Main Theorem 1.0.1. Let
![]() $\kappa $
be an inaccessible cardinal and suppose
$\kappa $
be an inaccessible cardinal and suppose
![]() $\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
.
$\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
.
-
• The minimum model of
 $\mathsf {GB}$
over
$\mathsf {GB}$
over
 $\mathrm {V}_\kappa $
is bi-interpretable with a certain extension adding a Cohen-generic class of ordinals. Thus,
$\mathrm {V}_\kappa $
is bi-interpretable with a certain extension adding a Cohen-generic class of ordinals. Thus,
 $\mathsf {GB}$
is not semantically tight.
$\mathsf {GB}$
is not semantically tight. -
• Let
 $k \ge 1$
. The minimum model of
$k \ge 1$
. The minimum model of
 $\mathsf {KM}_k$
over
$\mathsf {KM}_k$
over
 $\mathrm {V}_\kappa $
is bi-interpretable with a certain extension adding a Cohen-generic class of ordinals. Thus,
$\mathrm {V}_\kappa $
is bi-interpretable with a certain extension adding a Cohen-generic class of ordinals. Thus,
 $\mathsf {KM}_k$
is not semantically tight.
$\mathsf {KM}_k$
is not semantically tight.
We then build on these to show that, indeed, these theories are not tight, and that the same is true for subsystems of
![]() $\mathsf {Z}_2$
. The failure of tightness should be seen as a uniform version of the failure of semantic tightness.
$\mathsf {Z}_2$
. The failure of tightness should be seen as a uniform version of the failure of semantic tightness.
Main Theorem 1.0.2. The following theories are not tight
![]() $:$
$:$
-
•
 $\mathsf {GB};$
$\mathsf {GB};$
-
•
 $\mathsf {KM}_k$
for
$\mathsf {KM}_k$
for
 $k \ge 1;$
$k \ge 1;$
-
•
 $\mathsf {KM}_k + \Sigma ^1_k$
-Class Collection, for
$\mathsf {KM}_k + \Sigma ^1_k$
-Class Collection, for
 $k \ge 1;$
and
$k \ge 1;$
and -
• any of the above theories plus the schema of Replacement for all second-order formulae.
While our primary interest is in class theories, our methods are flexible enough to also apply to subsystems of second-order arithmetic.
Main Theorem 1.0.3. The following theories are not tight
![]() $:$
$:$
-
•
 $\mathsf {ACA}_0;$
$\mathsf {ACA}_0;$
-
•
 $\Pi _{k}^1\text {-}\mathsf {CA}_0$
for
$\Pi _{k}^1\text {-}\mathsf {CA}_0$
for
 $k \ge 1;$
$k \ge 1;$
-
•
 $\Sigma _{k}^1\text {-}\mathsf {AC}_0$
for
$\Sigma _{k}^1\text {-}\mathsf {AC}_0$
for
 $k \ge 1;$
and
$k \ge 1;$
and -
• any of the above theories plus the full Induction schema, i.e., the theories
 $\mathsf {ACA}$
,
$\mathsf {ACA}$
,
 $\Pi _{k}^1\text {-}\mathsf {CA}$
, and
$\Pi _{k}^1\text {-}\mathsf {CA}$
, and
 $\Sigma _{k}^1\text {-}\mathsf {AC}$
.
$\Sigma _{k}^1\text {-}\mathsf {AC}$
.
In forthcoming work, Enayat [Reference Enayat7] independently investigated the nontightness of fragments of
![]() $\mathsf {KM}$
and
$\mathsf {KM}$
and
![]() $\mathsf {Z}_2$
. He showed that finitely axiomatizable subtheories of these are not tight. That gives an alternate proof of the nontightness of
$\mathsf {Z}_2$
. He showed that finitely axiomatizable subtheories of these are not tight. That gives an alternate proof of the nontightness of
![]() $\mathsf {GB}$
,
$\mathsf {GB}$
,
![]() $\mathsf {KM}_k$
,
$\mathsf {KM}_k$
,
![]() $\mathsf {ACA}_0$
, and
$\mathsf {ACA}_0$
, and
![]() $\Pi _{k}^1\text {-}\mathsf {CA}_0$
, as well as the versions with Class Collection or
$\Pi _{k}^1\text {-}\mathsf {CA}_0$
, as well as the versions with Class Collection or
![]() $\mathsf {AC}$
. But the second-order Replacement schema and the full Induction schema are not finitely axiomatizable, so his methods don’t apply to the theories with those schemata.
$\mathsf {AC}$
. But the second-order Replacement schema and the full Induction schema are not finitely axiomatizable, so his methods don’t apply to the theories with those schemata.
We present the semantic non-tightness (Section 3) and non-tightness (Section 4) results for class theory separately. The constructions for non-tightness amounts to more difficult variants of the constructions for semantic non-tightness, generalized to apply to a wider class of models, including nonstandard models, so we present the easier constructions first. Additionally, the constructions over
![]() $\mathrm {V}_\kappa $
may be of interest to the set theorist with no interest in nonstandard models, and we wish to be accommodating to any such reader. In Section 5, we explore how to apply the same technique to subsystems of second-order arithmetic. And in Section 6 we briefly discuss the extent to which our constructions generalize and what questions remain open.
$\mathrm {V}_\kappa $
may be of interest to the set theorist with no interest in nonstandard models, and we wish to be accommodating to any such reader. In Section 5, we explore how to apply the same technique to subsystems of second-order arithmetic. And in Section 6 we briefly discuss the extent to which our constructions generalize and what questions remain open.
Before these sections we recall some definitions and basic facts about class theory.
2 Review of class theories and class forcing
In this paper we look at class theories, also called second-order set theories, those set theories that have proper classes as objects in their domains of discourse. We will use a two-sorted approach, writing a model as, e.g.,
![]() $(M,\mathcal {X})$
with M being the sets of the model and
$(M,\mathcal {X})$
with M being the sets of the model and
![]() $\mathcal {X}$
being the classes of the model. Following standard convention, when writing formulae in the language of class theory we will use lowercase variables for sets and uppercase variables for classes. For example,
$\mathcal {X}$
being the classes of the model. Following standard convention, when writing formulae in the language of class theory we will use lowercase variables for sets and uppercase variables for classes. For example,
![]() $\forall x \exists Y \forall z\ (z \in x \Leftrightarrow z \in Y)$
asserts that every set is co-extensional with some class, a trivial consequence of First-Order Comprehension.
$\forall x \exists Y \forall z\ (z \in x \Leftrightarrow z \in Y)$
asserts that every set is co-extensional with some class, a trivial consequence of First-Order Comprehension.
If a formula only quantifies over sets—but possibly has class parameters—we call it first-order. The class of first-order formulae is denoted with any of
![]() $\Sigma ^1_0$
,
$\Sigma ^1_0$
,
![]() $\Pi ^1_0$
, or
$\Pi ^1_0$
, or
![]() $\Delta ^1_0$
. From the first-order formulae we build up the hierarchy of
$\Delta ^1_0$
. From the first-order formulae we build up the hierarchy of
![]() $\Sigma ^1_k$
and
$\Sigma ^1_k$
and
![]() $\Pi ^1_k$
formulae by adding class quantifiers in the way familiar to any logician. Namely, a
$\Pi ^1_k$
formulae by adding class quantifiers in the way familiar to any logician. Namely, a
![]() $\Sigma ^1_k$
formula is of the form
$\Sigma ^1_k$
formula is of the form
![]() $\exists \bar X_1 \cdots \forall \bar X_k \varphi (\bar X_1, \ldots \bar X_k)$
, where
$\exists \bar X_1 \cdots \forall \bar X_k \varphi (\bar X_1, \ldots \bar X_k)$
, where
![]() $\varphi $
is first-order and there are k many blocks of alternating class quantifiers, while a
$\varphi $
is first-order and there are k many blocks of alternating class quantifiers, while a
![]() $\Pi ^1_k$
formula is of the form
$\Pi ^1_k$
formula is of the form
![]() $\forall \bar X_1 \cdots \exists \bar X_k \varphi (\bar X_1, \ldots \bar X_k)$
, again with first-order
$\forall \bar X_1 \cdots \exists \bar X_k \varphi (\bar X_1, \ldots \bar X_k)$
, again with first-order
![]() $\varphi $
and k many blocks of alternating class quantifiers.
$\varphi $
and k many blocks of alternating class quantifiers.
Definition 2.0.1.
Gödel–Bernays class theory
![]() $\mathsf {GB}$
is axiomatized by the following.
$\mathsf {GB}$
is axiomatized by the following.
-
•
 $\mathsf {ZFC}$
for classes;Footnote
8
$\mathsf {ZFC}$
for classes;Footnote
8
-
• Class Extensionality, asserting that two classes are equal if and only if they have the same elements;
-
• Class Replacement, asserting that the image of a set under a class function is always a set; and
-
• First-Order Comprehension, asserting that classes can be defined using comprehension for first-order formulae. More precisely, this axiom schema has as instances the universal closure of
for each first-order formula $$\begin{align*}\exists X\ X = \{ y : \varphi(y,\bar P) \} \end{align*}$$
$$\begin{align*}\exists X\ X = \{ y : \varphi(y,\bar P) \} \end{align*}$$
 $\varphi $
.
$\varphi $
.
If we add to
![]() $\mathsf {GB}$
Full Comprehension, viz. the instances of Comprehension for any formula in the language of class theory, we get Kelley–Morse class theory
$\mathsf {GB}$
Full Comprehension, viz. the instances of Comprehension for any formula in the language of class theory, we get Kelley–Morse class theory
![]() $\mathsf {KM}$
. For finite
$\mathsf {KM}$
. For finite
![]() $k \ge 1$
, adding
$k \ge 1$
, adding
![]() $\Sigma ^1_k$
-Comprehension—Comprehension for
$\Sigma ^1_k$
-Comprehension—Comprehension for
![]() $\Sigma ^1_k$
formulae—gives the theory we will call
$\Sigma ^1_k$
formulae—gives the theory we will call
![]() $\mathsf {KM}_k$
.
$\mathsf {KM}_k$
.
For some purposes
![]() $\mathsf {KM}$
is insufficient, and needs to be extended by a version of Collection for classes.Footnote
9
It will be convenient in this paper to work with this stronger variant (but not stronger in consistency strength). Using a stronger version will not harm our results since tightness is preserved by extension in the same language.
$\mathsf {KM}$
is insufficient, and needs to be extended by a version of Collection for classes.Footnote
9
It will be convenient in this paper to work with this stronger variant (but not stronger in consistency strength). Using a stronger version will not harm our results since tightness is preserved by extension in the same language.
A hyperclass is a collection of classes. Formally these do not exist in our models similar to how classes formally do not exist as objects in
![]() $\mathsf {ZFC}$
. However, some hyperclasses we can code with an individual class.
$\mathsf {ZFC}$
. However, some hyperclasses we can code with an individual class.
Definition 2.0.2. A code for a hyperclass is a class of ordered pairs. We say that a hyperclass
![]() $\mathcal {A}$
is coded if there is a code A so that
$\mathcal {A}$
is coded if there is a code A so that
where
![]() $(A)_i = \{ x : (i,x) \in A \}$
is the i-th slice of A.
$(A)_i = \{ x : (i,x) \in A \}$
is the i-th slice of A.
Definition 2.0.3. The Class Collection (
![]() $\mathsf {CC}$
) axiom schema asserts that if for each set there is a class satisfying some property, then we can collect witnesses classes into a single coded hyperclass.Footnote
10
Formally, instances of this schema are the universal closure of
$\mathsf {CC}$
) axiom schema asserts that if for each set there is a class satisfying some property, then we can collect witnesses classes into a single coded hyperclass.Footnote
10
Formally, instances of this schema are the universal closure of
where
![]() $\varphi $
ranges across all formulae in the language of class theory. If we restrict this schema to
$\varphi $
ranges across all formulae in the language of class theory. If we restrict this schema to
![]() $\Sigma ^1_k$
formulae we get
$\Sigma ^1_k$
formulae we get
![]() $\Sigma ^1_k$
-Class Collection (
$\Sigma ^1_k$
-Class Collection (
![]() $\Sigma _{k}^1\text {-}\mathsf {CC}$
).
$\Sigma _{k}^1\text {-}\mathsf {CC}$
).
Marek and Mostowski [Reference Marek, Mostowski, Müller, Oberschelp and Potthoff24, Theorem 2.5] showed that given any model of
![]() $\mathsf {KM}$
you can thin down the classes to get a model of
$\mathsf {KM}$
you can thin down the classes to get a model of
![]() $\mathsf {KMCC} = \mathsf {KM} + \mathsf {CC}$
with the same sets. Ratajczyk [Reference Ratajczyk31] built on their work to show that given any model of
$\mathsf {KMCC} = \mathsf {KM} + \mathsf {CC}$
with the same sets. Ratajczyk [Reference Ratajczyk31] built on their work to show that given any model of
![]() $\mathsf {KM}_k$
you can thin down the classes to get a model of
$\mathsf {KM}_k$
you can thin down the classes to get a model of
![]() $\mathsf {KMCC}_k = \mathsf {KM}_k + \Sigma _{k}^1\text {-}\mathsf {CC}$
with the same sets, where
$\mathsf {KMCC}_k = \mathsf {KM}_k + \Sigma _{k}^1\text {-}\mathsf {CC}$
with the same sets, where
![]() $k> 0$
.
$k> 0$
.
Just as Collection yields that every formula in the language of set theory is equivalent to one in the Lévy hierarchy,
![]() $\mathsf {CC}$
yields that every formula in the language of class theory is equivalent to a
$\mathsf {CC}$
yields that every formula in the language of class theory is equivalent to a
![]() $\Sigma ^1_k$
formula for some k. So the theories
$\Sigma ^1_k$
formula for some k. So the theories
![]() $\mathsf {KMCC}_k$
give a hierarchy of stronger and stronger theories which in the union give the full theory
$\mathsf {KMCC}_k$
give a hierarchy of stronger and stronger theories which in the union give the full theory
![]() $\mathsf {KMCC}$
.
$\mathsf {KMCC}$
.
2.1 Bi-interpretability with first-order set theory
For some of our results it will be convenient to work with first-order set theories rather than class theories. The construction behind the more difficult direction of these bi-interpretations goes back to Scott [Reference Scott32]. The key observation is that the Foundation axiom implies that every set x is determined by the isomorphism type of
![]() $(\operatorname {\mathrm {TC}}(\{x\}),\in )$
. As such, sets can be represented with isomorphism classes of well-founded, extensional directed graphs with a maximum element. In this way a model of
$(\operatorname {\mathrm {TC}}(\{x\}),\in )$
. As such, sets can be represented with isomorphism classes of well-founded, extensional directed graphs with a maximum element. In this way a model of
![]() $\mathsf {GB}$
can represent sets of rank
$\mathsf {GB}$
can represent sets of rank
![]() $\mathord {>}\mathrm {Ord}$
. To have a name, call this construction the unrolling construction and refer to the model of first-order set theory obtained as the unrolled model.
$\mathord {>}\mathrm {Ord}$
. To have a name, call this construction the unrolling construction and refer to the model of first-order set theory obtained as the unrolled model.
Theorem 2.1.1 [Reference Marek, Mostowski, Müller, Oberschelp and Potthoff24]
![]() $\mathsf {KMCC}$
and
$\mathsf {KMCC}$
and
![]() $\mathsf {ZFC}^-$
plus “there is a largest cardinal, and it is inaccessible” are bi-interpretable.Footnote
11
$\mathsf {ZFC}^-$
plus “there is a largest cardinal, and it is inaccessible” are bi-interpretable.Footnote
11
Denote this latter theory by
![]() $\mathsf {ZFC}^-_{\mathrm I}$
. Working in
$\mathsf {ZFC}^-_{\mathrm I}$
. Working in
![]() $\mathsf {ZFC}^-_{\mathrm I}$
let
$\mathsf {ZFC}^-_{\mathrm I}$
let
![]() $\kappa $
denote the largest cardinal. For these bi-interpretability results,
$\kappa $
denote the largest cardinal. For these bi-interpretability results,
![]() $\mathrm {V}$
of the model of class theory is isomorphic to
$\mathrm {V}$
of the model of class theory is isomorphic to
![]() $\mathrm {V}_\kappa $
of the unrolled model of
$\mathrm {V}_\kappa $
of the unrolled model of
![]() $\mathsf {ZFC}^-_{\mathrm I}$
. That is, the sets are fixed and the bi-interpretation is entirely about what happens in the classes.
$\mathsf {ZFC}^-_{\mathrm I}$
. That is, the sets are fixed and the bi-interpretation is entirely about what happens in the classes.
Doing the construction more carefully you can get versions of this result for restricted amounts of Comprehension. Here, let
![]() $\mathsf {ZFC}^-_{\mathrm {I},k}$
denote the theory obtained from
$\mathsf {ZFC}^-_{\mathrm {I},k}$
denote the theory obtained from
![]() $\mathsf {ZFC}^-_{\mathrm I}$
by restricting the Collection and Separation schemata to
$\mathsf {ZFC}^-_{\mathrm I}$
by restricting the Collection and Separation schemata to
![]() $\Sigma _k$
formulae.
$\Sigma _k$
formulae.
Theorem 2.1.2 [Reference Ratajczyk31]
The following pair of theories are bi-interpretable, for
![]() $k \ge 1$
.
$k \ge 1$
.
-
•
 $\mathsf {KMCC}_k$
and
$\mathsf {KMCC}_k$
and
 $\mathsf {ZFC}^-_{\mathrm {I},k}$
.
$\mathsf {ZFC}^-_{\mathrm {I},k}$
.
The reader who desires to read through the construction in detail is referred to the second author’s dissertation [Reference Williams40].
The main utility of these bi-interpretation results is that they allow us to use known facts about models of first-order set theory to draw conclusions about models of class theory. Additionally, some arguments become easier to formulate in that context, since we have access to von Neumann ordinals, the Mostowski collapse theorem, and so on, whereas with classes we don’t have direct access to these powerful tools.
2.2 Class forcing
We will use class forcing over models of
![]() $\mathsf {KMCC}_k$
. Because the theory of this is less well-known than over models of
$\mathsf {KMCC}_k$
. Because the theory of this is less well-known than over models of
![]() $\mathsf {KM}$
or
$\mathsf {KM}$
or
![]() $\mathsf {GB}$
, we recall the important facts here. Let’s begin by addressing nonstandard models.
$\mathsf {GB}$
, we recall the important facts here. Let’s begin by addressing nonstandard models.
With a transitive model of set theory, given a generic G you can interpret all
![]() $\mathbb {P}$
-names via an induction external to the model. If a model of set theory is ill-founded, we cannot do that. Instead we need an approach similar to the Boolean ultrapower approach. The atomic forcing relations
$\mathbb {P}$
-names via an induction external to the model. If a model of set theory is ill-founded, we cannot do that. Instead we need an approach similar to the Boolean ultrapower approach. The atomic forcing relations
![]() $p \Vdash \sigma = \tau $
and
$p \Vdash \sigma = \tau $
and
![]() $p \Vdash \sigma \in \tau $
yield the equivalence relation
$p \Vdash \sigma \in \tau $
yield the equivalence relation
![]() $=_G$
defined as
$=_G$
defined as
![]() $\sigma =_G \tau $
if and only if
$\sigma =_G \tau $
if and only if
![]() $p \Vdash \sigma = \tau $
for some
$p \Vdash \sigma = \tau $
for some
![]() $p \in G$
and a similarly defined congruence
$p \in G$
and a similarly defined congruence
![]() $\in _G$
modulo
$\in _G$
modulo
![]() $=_G$
. Quotienting the
$=_G$
. Quotienting the
![]() $\mathbb {P}$
-names by
$\mathbb {P}$
-names by
![]() $=_G$
and using
$=_G$
and using
![]() $\in _G$
as the membership relation gives the forcing extension. Identifying the ground model with the collection of
$\in _G$
as the membership relation gives the forcing extension. Identifying the ground model with the collection of
![]() $\check x/\mathord {=_G}$
for check names
$\check x/\mathord {=_G}$
for check names
![]() $\check x$
, we get the forcing extension as a genuine extension. It is straightforward to check that in case you start with a transitive model, this produces a model isomorphic to the one obtained by the external induction. The usual lemmata about forcing can be proved in this context.Footnote
12
$\check x$
, we get the forcing extension as a genuine extension. It is straightforward to check that in case you start with a transitive model, this produces a model isomorphic to the one obtained by the external induction. The usual lemmata about forcing can be proved in this context.Footnote
12
Theorem 2.2.1 (Stanley, Friedman [Reference Friedman14, Reference Stanley34])
![]() $\mathsf {GB}$
proves that pretame class forcings satisfy the forcing theorem for first-order formulae, viz. that the relations
$\mathsf {GB}$
proves that pretame class forcings satisfy the forcing theorem for first-order formulae, viz. that the relations
![]() $p \Vdash \varphi (\sigma ,\ldots )$
are classes for each first-order formula
$p \Vdash \varphi (\sigma ,\ldots )$
are classes for each first-order formula
![]() $\varphi $
.
$\varphi $
.
Corollary 2.2.2. Forcing with a tame class forcing preserves all axioms of
![]() $\mathsf {GB}$
or
$\mathsf {GB}$
or
![]() $\mathsf {KM}$
.
$\mathsf {KM}$
.
We elide the technicalities of tameness and pretameness, and point the reader to [Reference Friedman14] or [Reference Antos, Gitman, Daghighi, Rezus, Pourmahdian, Gabbay and Fitting2]. What is needed for our purposes is that
![]() $\mathrm {Add}(\mathrm {Ord},1)$
, the forcing to add a Cohen-generic class of ordinals, is tame.
$\mathrm {Add}(\mathrm {Ord},1)$
, the forcing to add a Cohen-generic class of ordinals, is tame.
Theorem 2.2.3. Let
![]() $k \ge 1$
. Forcing with a tame class forcing preserves all axioms of
$k \ge 1$
. Forcing with a tame class forcing preserves all axioms of
![]() $\mathsf {KMCC}_k$
.
$\mathsf {KMCC}_k$
.
Proof Sketch
One way to prove this goes through the bi-interpretability with first-order set theory. Knowing that set forcing preserves
![]() $\mathsf {ZFC}^-_k$
, with a little work one concludes tame class forcing preserves
$\mathsf {ZFC}^-_k$
, with a little work one concludes tame class forcing preserves
![]() $\mathsf {KMCC}_k$
.
$\mathsf {KMCC}_k$
.
Alternatively, one can prove this directly within class theory. To prove
![]() $\Sigma ^1_k$
-Comprehension and Class Collection, first you need to prove that the forcing relations for
$\Sigma ^1_k$
-Comprehension and Class Collection, first you need to prove that the forcing relations for
![]() $\Sigma ^1_k$
-formulae are classes. Note that this uses
$\Sigma ^1_k$
-formulae are classes. Note that this uses
![]() $\Sigma _{k}^1\text {-}\mathsf {CC}$
to be able to pull the set quantifiers expressing “densely many conditions force such and such” inside class quantifiers, so you get a
$\Sigma _{k}^1\text {-}\mathsf {CC}$
to be able to pull the set quantifiers expressing “densely many conditions force such and such” inside class quantifiers, so you get a
![]() $\Sigma ^1_k$
-definition for the forcing relations. (Compare to, in the
$\Sigma ^1_k$
-definition for the forcing relations. (Compare to, in the
![]() $\mathsf {ZF}$
context, how replacement is used to pull bounded quantifiers inside to get that the forcing relation for a
$\mathsf {ZF}$
context, how replacement is used to pull bounded quantifiers inside to get that the forcing relation for a
![]() $\Sigma _k$
formula is
$\Sigma _k$
formula is
![]() $\Sigma _k$
.) Once you know these forcing relations are classes, you then prove the preservation of the axioms in the usual way.
$\Sigma _k$
.) Once you know these forcing relations are classes, you then prove the preservation of the axioms in the usual way.
Definition 2.2.4. Suppose
![]() $(M,\mathcal {X})$
and
$(M,\mathcal {X})$
and
![]() $(M,\mathcal {Y})$
are two models of class theory with the same sets M. Say that
$(M,\mathcal {Y})$
are two models of class theory with the same sets M. Say that
![]() $(M,\mathcal {Y})$
is a width-extension of
$(M,\mathcal {Y})$
is a width-extension of
![]() $(M,\mathcal {X})$
if
$(M,\mathcal {X})$
if
![]() $\mathcal {X} \subseteq \mathcal {Y}$
and for every well-order
$\mathcal {X} \subseteq \mathcal {Y}$
and for every well-order
![]() $\Gamma \in \mathcal {Y}$
there is
$\Gamma \in \mathcal {Y}$
there is
![]() $\Gamma ' \in \mathcal {X}$
so that
$\Gamma ' \in \mathcal {X}$
so that
![]() $(M,\mathcal {Y})$
has an isomorphism
$(M,\mathcal {Y})$
has an isomorphism
![]() $\Gamma \cong \Gamma '$
.
$\Gamma \cong \Gamma '$
.
This notion is a class theoretic cousin of the familiar notion in first-order set theory of an extension which does not contain any new ordinals. As in the
![]() $\mathsf {ZF}$
context, forcing gives a width-extension (assuming strong enough axioms in the ground model).
$\mathsf {ZF}$
context, forcing gives a width-extension (assuming strong enough axioms in the ground model).
Theorem 2.2.5. Let
![]() $k \ge 1$
. Forcing over a model of
$k \ge 1$
. Forcing over a model of
![]() $\mathsf {KMCC}_k$
with a pretame forcing produces a width extension.
$\mathsf {KMCC}_k$
with a pretame forcing produces a width extension.
Proof Hamkins and Woodin [Reference Hamkins and Woodin20] proved that pretame forcing over a model of Open Class Determinancy cannot add new ordertypes for well-orders. Since
![]() $\Sigma ^1_1$
-Comprehension is enough to prove determinancy for open class games [Reference Gitman, Hamkins, Caicedo, Cummings, Koellner and Larson15], this gives the result.
$\Sigma ^1_1$
-Comprehension is enough to prove determinancy for open class games [Reference Gitman, Hamkins, Caicedo, Cummings, Koellner and Larson15], this gives the result.
Alternatively, one can prove this via the bi-interpretability with first-order set theory, using that forcing over a model of
![]() $\mathsf {ZFC}^-_1$
cannot add new ordinals.
$\mathsf {ZFC}^-_1$
cannot add new ordinals.
As an aside, we remark that it is open whether
![]() $\mathsf {KMCC}_1$
is necessary for this result.
$\mathsf {KMCC}_1$
is necessary for this result.
Question 2.2.6. Does
![]() $\mathsf {GB}$
prove that every pretame forcing extension is a width extension?
$\mathsf {GB}$
prove that every pretame forcing extension is a width extension?
3 Semantic non-tightness in class theory
In this section we show that certain fragments of
![]() $\mathsf {KM}$
fail to be semantically tight. All models considered will have the same sets. Namely, they will be
$\mathsf {KM}$
fail to be semantically tight. All models considered will have the same sets. Namely, they will be
![]() $\mathrm {V}_\kappa $
for a fixed inaccessible cardinal
$\mathrm {V}_\kappa $
for a fixed inaccessible cardinal
![]() $\kappa $
, and we will assume that
$\kappa $
, and we will assume that
![]() $\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
. (It is easy to arrange such by forcing, if necessary. Alternatively, this can be obtained by restricting down to an inner model.)
$\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
. (It is easy to arrange such by forcing, if necessary. Alternatively, this can be obtained by restricting down to an inner model.)
It is well known that satisfying
![]() $\mathrm {V} = \mathrm {HOD}$
is equivalent to having a definable (without parameters) global well-order. We will use the slightly stronger fact that there is a uniform definition which works for any model of
$\mathrm {V} = \mathrm {HOD}$
is equivalent to having a definable (without parameters) global well-order. We will use the slightly stronger fact that there is a uniform definition which works for any model of
![]() $\mathrm {V} = \mathrm {HOD}$
. Namely,
$\mathrm {V} = \mathrm {HOD}$
. Namely,
![]() $\mathrm {V} = \mathrm {HOD}$
asserts that every set is definable in some
$\mathrm {V} = \mathrm {HOD}$
asserts that every set is definable in some
![]() $\mathrm {V}_\beta $
using some ordinal parameter
$\mathrm {V}_\beta $
using some ordinal parameter
![]() $\alpha $
. So if we order the sets x by the least
$\alpha $
. So if we order the sets x by the least
![]() $\beta $
, then the least formula
$\beta $
, then the least formula
![]() $\varphi (v_1,v_2)$
, then the least parameter
$\varphi (v_1,v_2)$
, then the least parameter
![]() $\alpha $
so that x is defined by
$\alpha $
so that x is defined by
![]() $\varphi $
in
$\varphi $
in
![]() $\mathrm {V}_\beta $
using parameter
$\mathrm {V}_\beta $
using parameter
![]() $\alpha $
, this gives a global well-order of the universe in ordertype
$\alpha $
, this gives a global well-order of the universe in ordertype
![]() $\mathrm {Ord}$
. We will call this the
$\mathrm {Ord}$
. We will call this the
![]() $\mathrm {HOD}$
-order, refer to
$\mathrm {HOD}$
-order, refer to
![]() $\mathrm {HOD}$
-least choices, and so on.
$\mathrm {HOD}$
-least choices, and so on.
3.1 Semantic non-tightness of
 $\mathsf {GB}$
$\mathsf {GB}$
The strategy for establishing the semantic non-tightness of
![]() $\mathsf {GB}$
is this. Using
$\mathsf {GB}$
is this. Using
![]() $\mathrm {V}_\kappa $
as the sets there is a minimum model of
$\mathrm {V}_\kappa $
as the sets there is a minimum model of
![]() $\mathsf {GB}$
, namely
$\mathsf {GB}$
, namely
![]() $(\mathrm {V}_\kappa , \operatorname {Def}(\mathrm {V}_\kappa ))$
where we append the first-order definable subsets of
$(\mathrm {V}_\kappa , \operatorname {Def}(\mathrm {V}_\kappa ))$
where we append the first-order definable subsets of
![]() $\mathrm {V}_\kappa $
to be the classes. By Tarski’s theorem on the undefinability of truth, being in
$\mathrm {V}_\kappa $
to be the classes. By Tarski’s theorem on the undefinability of truth, being in
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
cannot be first-order definable over
$\operatorname {Def}(\mathrm {V}_\kappa )$
cannot be first-order definable over
![]() $\mathrm {V}_\kappa $
. But it is second-order definable and indeed absolutely so. Moreover, we will produce a carefully defined
$\mathrm {V}_\kappa $
. But it is second-order definable and indeed absolutely so. Moreover, we will produce a carefully defined
![]() $\mathrm {C} \subseteq \kappa $
which is also absolutely second-order definable over
$\mathrm {C} \subseteq \kappa $
which is also absolutely second-order definable over
![]() $\mathrm {V}_\kappa $
. Our two bi-interpretable models of
$\mathrm {V}_\kappa $
. Our two bi-interpretable models of
![]() $\mathsf {GB}$
will then be
$\mathsf {GB}$
will then be
![]() $(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
and
$(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
and
![]() $(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C}))$
where
$(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C}))$
where
![]() $\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
denotes the hyperclass of subsets of
$\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
denotes the hyperclass of subsets of
![]() $\mathrm {V}_\kappa $
definable using
$\mathrm {V}_\kappa $
definable using
![]() $\mathrm {C}$
as a parameter.
$\mathrm {C}$
as a parameter.
Observation 3.1.1. The satisfaction predicate
![]() $\mathrm {T}$
for
$\mathrm {T}$
for
![]() $\mathrm {V}_\kappa $
is both
$\mathrm {V}_\kappa $
is both
![]() $\Sigma ^1_1$
and
$\Sigma ^1_1$
and
![]() $\Pi ^1_1$
definable over
$\Pi ^1_1$
definable over
![]() $\mathrm {V}_\kappa $
. If
$\mathrm {V}_\kappa $
. If
![]() $\mathcal {X} \subseteq \mathcal {P}(\mathrm {V}_\kappa )$
is any possible collection of classes which give a model of
$\mathcal {X} \subseteq \mathcal {P}(\mathrm {V}_\kappa )$
is any possible collection of classes which give a model of
![]() $\mathsf {GB}$
then
$\mathsf {GB}$
then
![]() $\mathcal {X}$
will correctly define
$\mathcal {X}$
will correctly define
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
The content of this observation can be traced back to Mostowski [Reference Mostowski25].
Proof To define
![]() $\mathrm {T}$
in a
$\mathrm {T}$
in a
![]() $\Sigma ^1_1$
way, we observe that it is the union of the
$\Sigma ^1_1$
way, we observe that it is the union of the
![]() $\Sigma _k$
-satisfaction predicates, and these all agree on their common domains. While the first-order definitions of these are progressively more complex as k increases, whether a class is a
$\Sigma _k$
-satisfaction predicates, and these all agree on their common domains. While the first-order definitions of these are progressively more complex as k increases, whether a class is a
![]() $\Sigma _k$
-satisfaction class is uniformly recognizable in k. Namely, S is the
$\Sigma _k$
-satisfaction class is uniformly recognizable in k. Namely, S is the
![]() $\Sigma _k$
-satisfaction class if it satisfies the Tarskian recursion on its domain and it judges the truth of all and only the
$\Sigma _k$
-satisfaction class if it satisfies the Tarskian recursion on its domain and it judges the truth of all and only the
![]() $\Sigma _k$
formulae. To define
$\Sigma _k$
formulae. To define
![]() $\mathrm {T}$
in a
$\mathrm {T}$
in a
![]() $\Pi ^1_1$
way,
$\Pi ^1_1$
way,
![]() $\varphi [\vec a] \in \mathrm {T}$
iff for any class S if S is a
$\varphi [\vec a] \in \mathrm {T}$
iff for any class S if S is a
![]() $\Sigma _k$
-satisfaction class and
$\Sigma _k$
-satisfaction class and
![]() $\varphi [\vec a]$
is in its domain, then S judges
$\varphi [\vec a]$
is in its domain, then S judges
![]() $\varphi [\vec a]$
to be true.
$\varphi [\vec a]$
to be true.
Observe that
![]() $\mathsf {GB}$
suffices to prove the
$\mathsf {GB}$
suffices to prove the
![]() $\Sigma _k$
-satisfaction classes exist. So these definitions work for any model of
$\Sigma _k$
-satisfaction classes exist. So these definitions work for any model of
![]() $\mathsf {GB}$
with
$\mathsf {GB}$
with
![]() $\mathrm {V}_\kappa $
as its sets. (Here we use that we are working over a transitive model and so there are only standard k to worry about.)
$\mathrm {V}_\kappa $
as its sets. (Here we use that we are working over a transitive model and so there are only standard k to worry about.)
While
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
is a hyperclass and thus cannot be a class in any model of class theory with
$\operatorname {Def}(\mathrm {V}_\kappa )$
is a hyperclass and thus cannot be a class in any model of class theory with
![]() $\mathrm {V}_\kappa $
as its sets, it can be coded by a single class.
$\mathrm {V}_\kappa $
as its sets, it can be coded by a single class.
Observation 3.1.2. After a minor reshuffling of coordinates,
![]() $\mathrm {T}$
is a code for
$\mathrm {T}$
is a code for
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
.
$\operatorname {Def}(\mathrm {V}_\kappa )$
.
Proof A class X is definable if and only if
![]() $X = \{ x : \varphi [x,\vec a] \in \mathrm {T} \}$
for some formula
$X = \{ x : \varphi [x,\vec a] \in \mathrm {T} \}$
for some formula
![]() $\varphi $
with parameters
$\varphi $
with parameters
![]() $\vec a$
. So by reshuffling coordinates in
$\vec a$
. So by reshuffling coordinates in
![]() $\mathrm {T}$
to consist of ordered pairs
$\mathrm {T}$
to consist of ordered pairs
![]() $((\varphi ,\vec a),x)$
we get a code for
$((\varphi ,\vec a),x)$
we get a code for
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
.
$\operatorname {Def}(\mathrm {V}_\kappa )$
.
We will slightly abuse notation and use
![]() $\mathrm {T}$
to refer both to the satisfaction class and to this code for
$\mathrm {T}$
to refer both to the satisfaction class and to this code for
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
. We will write
$\operatorname {Def}(\mathrm {V}_\kappa )$
. We will write
![]() $(\mathrm {T})_\xi $
to refer to the slice of
$(\mathrm {T})_\xi $
to refer to the slice of
![]() $\mathrm {T}$
corresponding to the
$\mathrm {T}$
corresponding to the
![]() $\xi $
-th pair
$\xi $
-th pair
![]() $(\varphi ,\vec a)$
in the
$(\varphi ,\vec a)$
in the
![]() $\mathrm {HOD}$
-order.
$\mathrm {HOD}$
-order.
If
![]() $\mathrm {C}$
is a second-order definable generic for a forcing
$\mathrm {C}$
is a second-order definable generic for a forcing
![]() $\mathbb {P} \in \operatorname {Def}(\mathrm {V}_\kappa )$
then similar results hold for
$\mathbb {P} \in \operatorname {Def}(\mathrm {V}_\kappa )$
then similar results hold for
![]() $\mathrm {T}(\mathrm {C})$
, the satisfaction class relative to
$\mathrm {T}(\mathrm {C})$
, the satisfaction class relative to
![]() $\mathrm {C}$
as a parameter, and
$\mathrm {C}$
as a parameter, and
![]() $\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
, the hyperclass of classes definable using
$\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
, the hyperclass of classes definable using
![]() $\mathrm {C}$
as a parameter.
$\mathrm {C}$
as a parameter.
Lemma 3.1.3. Suppose
![]() $\mathrm {C}$
is a generic over
$\mathrm {C}$
is a generic over
![]() $(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
for a forcing
$(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
for a forcing
![]() $\mathbb {P} \in \operatorname {Def}(\mathrm {V}_\kappa )$
, and
$\mathbb {P} \in \operatorname {Def}(\mathrm {V}_\kappa )$
, and
![]() $\mathrm {C}$
is second-order definable. Then,
$\mathrm {C}$
is second-order definable. Then,
![]() $\mathrm {T}(\mathrm {C})$
is definable, indeed definable in a uniform manner across all
$\mathrm {T}(\mathrm {C})$
is definable, indeed definable in a uniform manner across all
![]() $(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {GB}$
which define
$(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {GB}$
which define
![]() $\mathrm {C}$
the same. Moreover, after a minor reshuffling of coordinates
$\mathrm {C}$
the same. Moreover, after a minor reshuffling of coordinates
![]() $\mathrm {T}(\mathrm {C})$
is a code for
$\mathrm {T}(\mathrm {C})$
is a code for
![]() $\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
.
$\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
.
Proof The reason this isn’t completely trivial is that partial satisfaction classes relative to
![]() $\mathrm {C}$
will not be (first-order) definable unless
$\mathrm {C}$
will not be (first-order) definable unless
![]() $\mathbb {P}$
is trivial, and so we cannot just relativize the definition of
$\mathbb {P}$
is trivial, and so we cannot just relativize the definition of
![]() $\mathrm {T}$
. Instead, we use the forcing theorem:
$\mathrm {T}$
. Instead, we use the forcing theorem:
![]() $\varphi [\vec a] \in \mathrm {T}(\mathrm {C})$
if and only if there is
$\varphi [\vec a] \in \mathrm {T}(\mathrm {C})$
if and only if there is
![]() $p \in \mathrm {C}$
so that “
$p \in \mathrm {C}$
so that “
![]() $p \Vdash \varphi (\vec a,\check C)\text {"} \in \mathrm {T}$
. By the assumption that
$p \Vdash \varphi (\vec a,\check C)\text {"} \in \mathrm {T}$
. By the assumption that
![]() $\mathrm {C}$
is second-order definable we can express “there is
$\mathrm {C}$
is second-order definable we can express “there is
![]() $p \in \mathrm {C}$
so that….” This definition works across any
$p \in \mathrm {C}$
so that….” This definition works across any
![]() $(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {GB}$
which defines
$(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {GB}$
which defines
![]() $\mathrm {C}$
the same because
$\mathrm {C}$
the same because
![]() $\mathrm {T}$
is absolute. Finally, the same argument as with
$\mathrm {T}$
is absolute. Finally, the same argument as with
![]() $\mathrm {T}$
gives a code for the hyperclass
$\mathrm {T}$
gives a code for the hyperclass
![]() $\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
.
$\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
.
In particular, this lemma implies that “every class is definable from
![]() $\mathrm {C}$
” is a second-order definable property. We will write
$\mathrm {C}$
” is a second-order definable property. We will write
![]() $\mathrm {Class} = \operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
as an abbreviation for the second-order formula asserting this.
$\mathrm {Class} = \operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
as an abbreviation for the second-order formula asserting this.
It remains to determine how to give an absolute definition for a generic
![]() $\mathrm {C}$
. In brief, we will define
$\mathrm {C}$
. In brief, we will define
![]() $\mathrm {C}$
to be a carefully chosen Cohen generic subclass of
$\mathrm {C}$
to be a carefully chosen Cohen generic subclass of
![]() $\kappa $
, using the
$\kappa $
, using the
![]() $\mathrm {HOD}$
-order to ensure canonicity of any choices.
$\mathrm {HOD}$
-order to ensure canonicity of any choices.
Lemma 3.1.4. There is a second-order definition for
![]() $\mathrm {C} \subseteq \kappa $
which is Cohen-generic over
$\mathrm {C} \subseteq \kappa $
which is Cohen-generic over
![]() $(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
so that any
$(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
so that any
![]() $\mathsf {GB}$
model over
$\mathsf {GB}$
model over
![]() $\mathrm {V}_\kappa $
defines
$\mathrm {V}_\kappa $
defines
![]() $\mathrm {C}$
the same. Consequently, there is a second-order definition for
$\mathrm {C}$
the same. Consequently, there is a second-order definition for
![]() $\mathrm {T}(\mathrm {C})$
so that all
$\mathrm {T}(\mathrm {C})$
so that all
![]() $\mathsf {GB}$
models over
$\mathsf {GB}$
models over
![]() $\mathrm {V}_\kappa $
define
$\mathrm {V}_\kappa $
define
![]() $\mathrm {T}(\mathrm {C})$
the same.
$\mathrm {T}(\mathrm {C})$
the same.
The idea behind this lemma is originally due to Feferman [Reference Feferman10], who did the same construction in the context of arithmetic. See [Reference Odifreddi26–Reference Odifreddi28] for an exposition of Feferman’s work.
Proof Recall that the forcing
![]() $\mathrm {Add}(\kappa ,1)$
is
$\mathrm {Add}(\kappa ,1)$
is
![]() $\mathord {<}\kappa $
-closed and is first-order definable over
$\mathord {<}\kappa $
-closed and is first-order definable over
![]() $\mathrm {V}_\kappa $
. There are
$\mathrm {V}_\kappa $
. There are
![]() $\kappa $
many dense subsets of
$\kappa $
many dense subsets of
![]() $\mathrm {Add}(\kappa ,1)$
which appear in
$\mathrm {Add}(\kappa ,1)$
which appear in
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
, so we can meet them one at a time, using closure at limit stages. From
$\operatorname {Def}(\mathrm {V}_\kappa )$
, so we can meet them one at a time, using closure at limit stages. From
![]() $\mathrm {T}$
define a sequence
$\mathrm {T}$
define a sequence
![]() $\vec D = {\left \langle D_\xi : \xi \in \kappa \right \rangle }$
of all the dense classes in
$\vec D = {\left \langle D_\xi : \xi \in \kappa \right \rangle }$
of all the dense classes in
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
by ordering them by the
$\operatorname {Def}(\mathrm {V}_\kappa )$
by ordering them by the
![]() $\mathrm {HOD}$
-least pair
$\mathrm {HOD}$
-least pair
![]() $(\varphi ,\vec a)$
which gives a dense class. Note that
$(\varphi ,\vec a)$
which gives a dense class. Note that
![]() $\vec D$
is first-order definable from
$\vec D$
is first-order definable from
![]() $\mathrm {T}$
. Since
$\mathrm {T}$
. Since
![]() $\mathrm {T}$
is absolutely definable this means that all models of
$\mathrm {T}$
is absolutely definable this means that all models of
![]() $\mathsf {GB}$
over
$\mathsf {GB}$
over
![]() $\mathrm {V}_\kappa $
compute
$\mathrm {V}_\kappa $
compute
![]() $\vec D$
the same.
$\vec D$
the same.
The construction is done in
![]() $\kappa $
many steps. Start with
$\kappa $
many steps. Start with
![]() $p_0 = \emptyset $
. Having built
$p_0 = \emptyset $
. Having built
![]() $p_\xi $
define
$p_\xi $
define
![]() $p_{\xi +1}$
to be the
$p_{\xi +1}$
to be the
![]() $\mathrm {HOD}$
-least condition
$\mathrm {HOD}$
-least condition
![]() $< p_\xi $
which meets
$< p_\xi $
which meets
![]() $D_\xi $
. And if
$D_\xi $
. And if
![]() $\eta $
is limit then define
$\eta $
is limit then define
![]() $p_\eta = \bigcup _{\xi < \eta } p_\xi $
. Because
$p_\eta = \bigcup _{\xi < \eta } p_\xi $
. Because
![]() $\kappa $
is inaccessible we have that
$\kappa $
is inaccessible we have that
![]() $p_\eta \in \mathrm {V}_\kappa $
and thus we can continue the induction. Finally, set
$p_\eta \in \mathrm {V}_\kappa $
and thus we can continue the induction. Finally, set
![]() $\mathrm {C} = \bigcup _{\xi \in \kappa } p_\xi $
. Because any model of
$\mathrm {C} = \bigcup _{\xi \in \kappa } p_\xi $
. Because any model of
![]() $\mathsf {GB}$
over
$\mathsf {GB}$
over
![]() $\mathrm {V}_\kappa $
computes
$\mathrm {V}_\kappa $
computes
![]() $\vec D$
the same, inductively we can see that they all compute each
$\vec D$
the same, inductively we can see that they all compute each
![]() $p_\xi $
the same, whence they compute
$p_\xi $
the same, whence they compute
![]() $\mathrm {C}$
the same.
$\mathrm {C}$
the same.
We are now in a position to exhibit that
![]() $\mathsf {GB}$
is not semantically tight.
$\mathsf {GB}$
is not semantically tight.
Theorem 3.1.5. The two models
![]() $(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
and
$(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ))$
and
![]() $(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C}))$
of
$(\mathrm {V}_\kappa ,\operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C}))$
of
![]() $\mathsf {GB}$
, where
$\mathsf {GB}$
, where
![]() $\kappa $
is inaccessible,
$\kappa $
is inaccessible,
![]() $\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
, and
$\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
, and
![]() $\mathrm {C}$
is the generic defined as above, are bi-interpretable.Footnote
13
$\mathrm {C}$
is the generic defined as above, are bi-interpretable.Footnote
13
Corollary 3.1.6.
![]() $\mathsf {GB}$
is not semantically tight.
$\mathsf {GB}$
is not semantically tight.
Proof of Theorem
Let
![]() $\mathcal {X} = \operatorname {Def}(\mathrm {V}_\kappa )$
and
$\mathcal {X} = \operatorname {Def}(\mathrm {V}_\kappa )$
and
![]() $\mathcal {Y} = \operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
. Interpreting
$\mathcal {Y} = \operatorname {Def}(\mathrm {V}_\kappa ;\mathrm {C})$
. Interpreting
![]() $(\mathrm {V}_\kappa ,\mathcal {X})$
inside
$(\mathrm {V}_\kappa ,\mathcal {X})$
inside
![]() $(\mathrm {V}_\kappa ,\mathcal {Y})$
is simple. The interpretation, call it
$(\mathrm {V}_\kappa ,\mathcal {Y})$
is simple. The interpretation, call it
![]() $\mathcal {I}$
, is the identity on its domain, and
$\mathcal {I}$
, is the identity on its domain, and
![]() $\in ^{\mathcal {I}}$
is simply
$\in ^{\mathcal {I}}$
is simply
![]() $\in $
. The domain includes all of
$\in $
. The domain includes all of
![]() $\mathrm {V}_\kappa $
to be the sets of the interpreted model, but restricts the classes to only include those which are first-order definable. This domain is second-order definable because
$\mathrm {V}_\kappa $
to be the sets of the interpreted model, but restricts the classes to only include those which are first-order definable. This domain is second-order definable because
![]() $\mathrm {T}$
is second-order definable.
$\mathrm {T}$
is second-order definable.
The interpretation in the other direction, call it
![]() $\mathcal {J}$
, takes more care, since we need to refer to classes which are not actually in
$\mathcal {J}$
, takes more care, since we need to refer to classes which are not actually in
![]() $\mathcal {X}$
. For the sets of the interpreted model we will take all of
$\mathcal {X}$
. For the sets of the interpreted model we will take all of
![]() $\{0\} \times \mathrm {V}_\kappa $
and for the classes we will take a subset of
$\{0\} \times \mathrm {V}_\kappa $
and for the classes we will take a subset of
![]() $\{1\} \times \kappa $
. Specifically,
$\{1\} \times \kappa $
. Specifically,
![]() $(1,\xi )$
is in the domain of
$(1,\xi )$
is in the domain of
![]() $\mathcal {J}$
just in case
$\mathcal {J}$
just in case
![]() $(\mathrm {T}(\mathrm {C}))_\xi \ne (\mathrm {T}(\mathrm {C}))_\eta $
for all
$(\mathrm {T}(\mathrm {C}))_\xi \ne (\mathrm {T}(\mathrm {C}))_\eta $
for all
![]() $\eta < \xi $
, where the subscripts refer to the rank of the indices in the
$\eta < \xi $
, where the subscripts refer to the rank of the indices in the
![]() $\mathrm {HOD}$
-order. For sets,
$\mathrm {HOD}$
-order. For sets,
![]() $(0,x) \in ^{\mathcal {J}} (0,y)$
if and only if
$(0,x) \in ^{\mathcal {J}} (0,y)$
if and only if
![]() $x \in y$
. For set-class membership,
$x \in y$
. For set-class membership,
![]() $(0,x) \in ^{\mathcal {J}} (1,\eta )$
if and only if
$(0,x) \in ^{\mathcal {J}} (1,\eta )$
if and only if
![]() $x \in (\mathrm {T}(\mathrm {C}))_\eta $
. In effect, the interpretation is that each class in the extension is interpreted as (the index of) the first formula which defines it.
$x \in (\mathrm {T}(\mathrm {C}))_\eta $
. In effect, the interpretation is that each class in the extension is interpreted as (the index of) the first formula which defines it.
It is clear from the constructions that
![]() $\mathcal {I}(\mathrm {V}_\kappa ,\mathcal {Y}) = (\mathrm {V}_\kappa ,\mathcal {X})$
and
$\mathcal {I}(\mathrm {V}_\kappa ,\mathcal {Y}) = (\mathrm {V}_\kappa ,\mathcal {X})$
and
![]() $\mathcal {J}(\mathrm {V}_\kappa ,\mathcal {X}) \cong (\mathrm {V}_\kappa ,\mathcal {Y})$
. For one composition, work inside
$\mathcal {J}(\mathrm {V}_\kappa ,\mathcal {X}) \cong (\mathrm {V}_\kappa ,\mathcal {Y})$
. For one composition, work inside
![]() $(\mathrm {V}_\kappa ,\mathcal {X})$
. It is easy that
$(\mathrm {V}_\kappa ,\mathcal {X})$
. It is easy that
![]() $\mathcal {I}(\mathcal {J}(\mathrm {V}_\kappa ))$
is isomorphic to
$\mathcal {I}(\mathcal {J}(\mathrm {V}_\kappa ))$
is isomorphic to
![]() $\mathrm {V}_\kappa $
—just strip off the
$\mathrm {V}_\kappa $
—just strip off the
![]() $0$
in the first coordinate. For the classes, to define an isomorphism
$0$
in the first coordinate. For the classes, to define an isomorphism
![]() $\mathcal {X} \cong \mathcal {I}(\mathcal {J}(\mathcal {X}))$
, given a class X first query
$\mathcal {X} \cong \mathcal {I}(\mathcal {J}(\mathcal {X}))$
, given a class X first query
![]() $\mathrm {T}(\mathrm {C})$
to find the
$\mathrm {T}(\mathrm {C})$
to find the
![]() $\mathrm {HOD}$
-least formula which defines X. Call the index of this formula
$\mathrm {HOD}$
-least formula which defines X. Call the index of this formula
![]() $\xi $
. Then send X to
$\xi $
. Then send X to
![]() $(1,\xi )$
. This isomorphism is first-order definable from
$(1,\xi )$
. This isomorphism is first-order definable from
![]() $\mathrm {T}(\mathrm {C})$
, so it is second-order definable over
$\mathrm {T}(\mathrm {C})$
, so it is second-order definable over
![]() $(\mathrm {V}_\kappa ,\mathcal {X})$
, which correctly computes it. For the other composition, it is again easy that the sets of
$(\mathrm {V}_\kappa ,\mathcal {X})$
, which correctly computes it. For the other composition, it is again easy that the sets of
![]() $\mathcal {J} \circ \mathcal {I}$
are isomorphic to the sets in the ground model. For the classes, again do the same trick of looking for the
$\mathcal {J} \circ \mathcal {I}$
are isomorphic to the sets in the ground model. For the classes, again do the same trick of looking for the
![]() $\mathrm {HOD}$
-least slice of
$\mathrm {HOD}$
-least slice of
![]() $\mathrm {T}(\mathrm {C})$
which gives X.
$\mathrm {T}(\mathrm {C})$
which gives X.
3.2 Semantic non-tightness of
 $\mathsf {KM}_k$
$\mathsf {KM}_k$
Fix for the entirety of this section finite
![]() $k \ge 1$
.
$k \ge 1$
.
It will be convenient to work with the stronger theory
![]() $\mathsf {KMCC}_k$
. This gives a slight improvement to the conclusion that
$\mathsf {KMCC}_k$
. This gives a slight improvement to the conclusion that
![]() $\mathsf {KM}_k$
is not semantically tight, so that is no cost to pay. To show that
$\mathsf {KM}_k$
is not semantically tight, so that is no cost to pay. To show that
![]() $\mathsf {KMCC}_k$
is semantically non-tight we will follow the same strategy as in the previous subsection. One model of
$\mathsf {KMCC}_k$
is semantically non-tight we will follow the same strategy as in the previous subsection. One model of
![]() $\mathsf {KMCC}_k$
will be the minimum model of
$\mathsf {KMCC}_k$
will be the minimum model of
![]() $\mathsf {KMCC}_k$
over
$\mathsf {KMCC}_k$
over
![]() $\kappa $
and the other will be an extension of the minimum model by a canonically chosen Cohen generic.
$\kappa $
and the other will be an extension of the minimum model by a canonically chosen Cohen generic.
Fix finite
![]() $k \ge 1$
. Let
$k \ge 1$
. Let
![]() $\alpha> \kappa $
be the smallest ordinal so that
$\alpha> \kappa $
be the smallest ordinal so that
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
satisfies
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
satisfies
![]() $\Sigma _k$
-Collection and
$\Sigma _k$
-Collection and
![]() $\Sigma _k$
-Separation. By the assumption that
$\Sigma _k$
-Separation. By the assumption that
![]() $\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
, we have a definable global well-order in
$\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
, we have a definable global well-order in
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
, call it the
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
, call it the
![]() $\mathrm {L}(\mathrm {V}_\kappa )$
-order. Set
$\mathrm {L}(\mathrm {V}_\kappa )$
-order. Set
![]() $\mathcal {M}$
to consist of all subsets of
$\mathcal {M}$
to consist of all subsets of
![]() $\mathrm {V}_\kappa $
which appear as elements of
$\mathrm {V}_\kappa $
which appear as elements of
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. This
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. This
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
will be our minimum model of
$(\mathrm {V}_\kappa ,\mathcal {M})$
will be our minimum model of
![]() $\mathsf {KMCC}_k$
.
$\mathsf {KMCC}_k$
.
Lemma 3.2.1. The minimum model
![]() $(\mathrm {V}_\kappa ,\mathcal {M}) \models \mathsf {KMCC}_k$
.
$(\mathrm {V}_\kappa ,\mathcal {M}) \models \mathsf {KMCC}_k$
.
Proof It is immediate that the model satisfies Class Extensionality and Class Replacement. Consider a
![]() $\Sigma ^1_k$
-formula
$\Sigma ^1_k$
-formula
![]() $\varphi (x)$
, possibly with parameters from
$\varphi (x)$
, possibly with parameters from
![]() $\mathcal {M}$
. Inside
$\mathcal {M}$
. Inside
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
, the set
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
, the set
![]() $\{ x \in \mathrm {V}_\kappa : \mathrm {L}_\alpha (\mathrm {V}_\kappa ) \models \varphi (x)^{\mathcal {M}} \}$
exists by
$\{ x \in \mathrm {V}_\kappa : \mathrm {L}_\alpha (\mathrm {V}_\kappa ) \models \varphi (x)^{\mathcal {M}} \}$
exists by
![]() $\Sigma _k$
-Separation. But then this set is in
$\Sigma _k$
-Separation. But then this set is in
![]() $\mathcal {M}$
, establishing the instance of Comprehension for
$\mathcal {M}$
, establishing the instance of Comprehension for
![]() $\varphi $
. Now consider a
$\varphi $
. Now consider a
![]() $\Sigma ^1_k$
-formula
$\Sigma ^1_k$
-formula
![]() $\varphi (x,Y)$
, possibly with parameters from
$\varphi (x,Y)$
, possibly with parameters from
![]() $\mathcal {M}$
, and assume that for each
$\mathcal {M}$
, and assume that for each
![]() $x \in \mathrm {V}$
there is
$x \in \mathrm {V}$
there is
![]() $Y \in \mathcal {M}$
so that
$Y \in \mathcal {M}$
so that
![]() $(\mathrm {V}_\kappa ,\mathcal {M}) \models \varphi (x,Y)$
. By
$(\mathrm {V}_\kappa ,\mathcal {M}) \models \varphi (x,Y)$
. By
![]() $\Sigma _k$
-Collection in
$\Sigma _k$
-Collection in
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
we find therein a set
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
we find therein a set
![]() $b \subseteq \mathcal {P}(\mathrm {V}_\kappa )$
so that for each
$b \subseteq \mathcal {P}(\mathrm {V}_\kappa )$
so that for each
![]() $x \in \mathrm {V}_\kappa $
there is
$x \in \mathrm {V}_\kappa $
there is
![]() $Y \in b$
so that
$Y \in b$
so that
![]() $\varphi (x,Y)^{\mathcal {M}}$
. Because
$\varphi (x,Y)^{\mathcal {M}}$
. Because
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
has an injection
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
has an injection
![]() $f: b \to \kappa $
we can build the set
$f: b \to \kappa $
we can build the set
![]() $B = \{ (f(Y), y) : y \in Y \in b \}$
, which is in
$B = \{ (f(Y), y) : y \in Y \in b \}$
, which is in
![]() $\mathcal {M}$
. This B witnesses the instance of Class Collection for
$\mathcal {M}$
. This B witnesses the instance of Class Collection for
![]() $\varphi $
, completing the proof.
$\varphi $
, completing the proof.
While this is not necessary to produce non-isomorphic but bi-interpretable models of
![]() $\mathsf {KMCC}_k$
, we remark as an aside that this
$\mathsf {KMCC}_k$
, we remark as an aside that this
![]() $\mathcal {M}$
really does give a minimum model.
$\mathcal {M}$
really does give a minimum model.
Theorem 3.2.2 (Ratajcyk)
If
![]() $(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {KM}_k$
then
$(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {KM}_k$
then
![]() $\mathcal {M} \subseteq \mathcal {X}$
.
$\mathcal {M} \subseteq \mathcal {X}$
.
Proof By work of Ratajcyk [Reference Ratajczyk31], every model of
![]() $\mathsf {KM}_k$
contains a submodel with the same sets which satisfies
$\mathsf {KM}_k$
contains a submodel with the same sets which satisfies
![]() $\mathsf {KMCC}_k$
. So we may assume that
$\mathsf {KMCC}_k$
. So we may assume that
![]() $(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {KMCC}_k$
. Let
$(\mathrm {V}_\kappa ,\mathcal {X}) \models \mathsf {KMCC}_k$
. Let
![]() $M \models \mathsf {ZFC}^-_{\mathrm {I},k}$
be the unrolled model, obtained as discussed in Section 2.1. Because
$M \models \mathsf {ZFC}^-_{\mathrm {I},k}$
be the unrolled model, obtained as discussed in Section 2.1. Because
![]() $\kappa $
has uncountable cofinality,
$\kappa $
has uncountable cofinality,
![]() $(\mathrm {V}_\kappa ,\mathcal {X})$
is correct about which of its classes are well-founded. Thus, M is well-founded, and we assume without loss that M is transitive. By the leastness of
$(\mathrm {V}_\kappa ,\mathcal {X})$
is correct about which of its classes are well-founded. Thus, M is well-founded, and we assume without loss that M is transitive. By the leastness of
![]() $\alpha $
, we have
$\alpha $
, we have
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa ) \subseteq M$
and thus
$\mathrm {L}_\alpha (\mathrm {V}_\kappa ) \subseteq M$
and thus
![]() $\mathcal {M} \subseteq \mathcal {X}$
.
$\mathcal {M} \subseteq \mathcal {X}$
.
Next we need to see that we can define a code for
![]() $\mathcal {M}$
in such a way that different models of
$\mathcal {M}$
in such a way that different models of
![]() $\mathsf {KMCC}_k$
over
$\mathsf {KMCC}_k$
over
![]() $\mathrm {V}_\kappa $
will define the same code. First, let us work with
$\mathrm {V}_\kappa $
will define the same code. First, let us work with
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. We begin by highlighting an easy but useful fact.
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. We begin by highlighting an easy but useful fact.
Lemma 3.2.3. Over
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
there is a definable increasing cofinal map
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
there is a definable increasing cofinal map
![]() $\alpha \to \kappa $
. Consequently, any outer model of
$\alpha \to \kappa $
. Consequently, any outer model of
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
can define this map, with the same definition working uniformly across all outer models.
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
can define this map, with the same definition working uniformly across all outer models.
Proof Sketch
The argument combines two facts. First, because
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
doesn’t satisfy
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
doesn’t satisfy
![]() $\Sigma _{k+1}$
-Replacement, there is a definable cofinal map from some
$\Sigma _{k+1}$
-Replacement, there is a definable cofinal map from some
![]() $\xi < \alpha $
to
$\xi < \alpha $
to
![]() $\alpha $
. Second, because
$\alpha $
. Second, because
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
satisfies that every set injects into
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
satisfies that every set injects into
![]() $\kappa $
we may take
$\kappa $
we may take
![]() $\xi = \kappa $
. And it’s easy to get the map to be increasing.
$\xi = \kappa $
. And it’s easy to get the map to be increasing.
Once we have an increasing cofinal map
![]() $f: \kappa \to \alpha $
it is straightforward to define a bijection
$f: \kappa \to \alpha $
it is straightforward to define a bijection
![]() $\kappa \to \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. For each
$\kappa \to \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. For each
![]() $f(i)$
pick the
$f(i)$
pick the
![]() $\mathrm {L}(\mathrm {V}_\kappa )$
-least bijection
$\mathrm {L}(\mathrm {V}_\kappa )$
-least bijection
![]() $b_i : \kappa \to \mathrm {L}_{f(i)}$
. Combining these together we get a map
$b_i : \kappa \to \mathrm {L}_{f(i)}$
. Combining these together we get a map
![]() $\kappa \times \kappa \to \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
, and via a pairing function we may take the domain to be
$\kappa \times \kappa \to \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
, and via a pairing function we may take the domain to be
![]() $\kappa $
. To get a bijection we need to ensure everything in the codomain is hit only once, but this is easily done by only picking the least index. Writing down an explicit definition is tedious, but it is clear that this produces a definable map. One can think of this bijection as giving us uniform access to all of
$\kappa $
. To get a bijection we need to ensure everything in the codomain is hit only once, but this is easily done by only picking the least index. Writing down an explicit definition is tedious, but it is clear that this produces a definable map. One can think of this bijection as giving us uniform access to all of
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
.
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
.
But we want to work over
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
to get a uniform access to all of
$(\mathrm {V}_\kappa ,\mathcal {M})$
to get a uniform access to all of
![]() $\mathcal {M}$
, which requires some small adjustments.
$\mathcal {M}$
, which requires some small adjustments.
Corollary 3.2.4. Over
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
we can define, via a second-order formula, a code
$(\mathrm {V}_\kappa ,\mathcal {M})$
we can define, via a second-order formula, a code
![]() $\mathrm {T}_{\mathcal {M}}$
for
$\mathrm {T}_{\mathcal {M}}$
for
![]() $\mathcal {M}$
. Moreover, we can do this in such a way that any
$\mathcal {M}$
. Moreover, we can do this in such a way that any
![]() $(\mathrm {V}_\kappa , \mathcal {Y}) \models \mathsf {KMCC}_k$
which is a width-extension of
$(\mathrm {V}_\kappa , \mathcal {Y}) \models \mathsf {KMCC}_k$
which is a width-extension of
![]() $\mathcal {M}$
will define the same code
$\mathcal {M}$
will define the same code
![]() $\mathrm {T}_{\mathcal {M}}$
.
$\mathrm {T}_{\mathcal {M}}$
.
Proof Let
![]() $f : \kappa \to \alpha $
denote the definable, cofinal map defined above. The point is, we can mimic the definition of f inside
$f : \kappa \to \alpha $
denote the definable, cofinal map defined above. The point is, we can mimic the definition of f inside
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
. In some detail: There is an isomorphic copy of
$(\mathrm {V}_\kappa ,\mathcal {M})$
. In some detail: There is an isomorphic copy of
![]() $(\operatorname {\mathrm {TC}}(\{x\}), \mathord \in \upharpoonright \operatorname {\mathrm {TC}}(\{x\}))$
in
$(\operatorname {\mathrm {TC}}(\{x\}), \mathord \in \upharpoonright \operatorname {\mathrm {TC}}(\{x\}))$
in
![]() $\mathcal {M}$
for each
$\mathcal {M}$
for each
![]() $x \in \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. More, by Mostowski’s collapse lemma any extensional, well-founded relation with a maximum element in
$x \in \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
. More, by Mostowski’s collapse lemma any extensional, well-founded relation with a maximum element in
![]() $\mathcal {M}$
is isomorphic to the restriction of
$\mathcal {M}$
is isomorphic to the restriction of
![]() $\in $
to
$\in $
to
![]() $\operatorname {\mathrm {TC}}(\{x\})$
for some
$\operatorname {\mathrm {TC}}(\{x\})$
for some
![]() $x \in \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
.Footnote
14
In sum,
$x \in \mathrm {L}_\alpha (\mathrm {V}_\kappa )$
.Footnote
14
In sum,
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
can mimic quantification over
$(\mathrm {V}_\kappa ,\mathcal {M})$
can mimic quantification over
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
by quantifying over extensional, well-founded relations with a maximum element, and thus
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
by quantifying over extensional, well-founded relations with a maximum element, and thus
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
can mimic the definition of f.
$(\mathrm {V}_\kappa ,\mathcal {M})$
can mimic the definition of f.
We then define a code
![]() $\mathrm {T}_{\mathcal {M}} \subseteq \kappa \times \kappa \times \mathrm {V}_\kappa $
for
$\mathrm {T}_{\mathcal {M}} \subseteq \kappa \times \kappa \times \mathrm {V}_\kappa $
for
![]() $\mathcal {M}$
by putting
$\mathcal {M}$
by putting
![]() $(i,j,x)$
in
$(i,j,x)$
in
![]() $\mathrm {T}_{\mathcal {M}}$
if x is in the j-th element of
$\mathrm {T}_{\mathcal {M}}$
if x is in the j-th element of
![]() $\mathrm {L}_{f(i)}(\mathrm {V}_\kappa )$
according to the
$\mathrm {L}_{f(i)}(\mathrm {V}_\kappa )$
according to the
![]() $\mathrm {L}(\mathrm {V}_\kappa )$
-least enumeration of
$\mathrm {L}(\mathrm {V}_\kappa )$
-least enumeration of
![]() $\mathrm {L}_{f(i)}(\mathrm {V}_\kappa )$
. And this definition is absolute to width-extensions because width-extensions will define
$\mathrm {L}_{f(i)}(\mathrm {V}_\kappa )$
. And this definition is absolute to width-extensions because width-extensions will define
![]() $\mathrm {L}(\mathrm {V}_\kappa )$
the same and so define F the same.
$\mathrm {L}(\mathrm {V}_\kappa )$
the same and so define F the same.
Note that this definition for the code
![]() $\mathrm {T}_{\mathcal {M}}$
is not
$\mathrm {T}_{\mathcal {M}}$
is not
![]() $\Sigma ^1_k$
because the definition of f is logically too complex. Of course we cannot hope to find a
$\Sigma ^1_k$
because the definition of f is logically too complex. Of course we cannot hope to find a
![]() $\Sigma ^1_k$
definition. For if
$\Sigma ^1_k$
definition. For if
![]() $\mathrm {T}_{\mathcal {M}}$
were
$\mathrm {T}_{\mathcal {M}}$
were
![]() $\Sigma ^1_k$
definable then it would be an element of
$\Sigma ^1_k$
definable then it would be an element of
![]() $\mathcal {M}$
by
$\mathcal {M}$
by
![]() $\Sigma ^1_k$
-Comprehension, but then
$\Sigma ^1_k$
-Comprehension, but then
![]() $\mathrm {T}_{\mathcal {M}}$
would be an element of
$\mathrm {T}_{\mathcal {M}}$
would be an element of
![]() $\mathrm {L}_{\xi }(\mathrm {V}_\kappa )$
for some
$\mathrm {L}_{\xi }(\mathrm {V}_\kappa )$
for some
![]() $\xi < \alpha $
and so all of
$\xi < \alpha $
and so all of
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
would occur by stage
$\mathrm {L}_\alpha (\mathrm {V}_\kappa )$
would occur by stage
![]() $\xi $
. That would be absurd.
$\xi $
. That would be absurd.
Similar machinery works for relative constructibility. Given a class
![]() $\mathrm {C}$
over
$\mathrm {C}$
over
![]() $\mathrm {V}_\kappa $
, let
$\mathrm {V}_\kappa $
, let
![]() $\mathcal {M}(\mathrm {C})$
denote the subsets of
$\mathcal {M}(\mathrm {C})$
denote the subsets of
![]() $\mathrm {V}_\kappa $
which appear in
$\mathrm {V}_\kappa $
which appear in
![]() $\mathrm {L}_\alpha (\mathrm {V}_\kappa ,\mathrm {C})$
. As in the
$\mathrm {L}_\alpha (\mathrm {V}_\kappa ,\mathrm {C})$
. As in the
![]() $\mathsf {GB}$
case, if
$\mathsf {GB}$
case, if
![]() $\mathrm {C}$
is a generic for a forcing in
$\mathrm {C}$
is a generic for a forcing in
![]() $\mathcal {M}$
then we can define a canonical choice of a code
$\mathcal {M}$
then we can define a canonical choice of a code
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
for
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
for
![]() $\mathcal {M}(\mathrm {C})$
.
$\mathcal {M}(\mathrm {C})$
.
Lemma 3.2.5. Suppose
![]() $\mathrm {C} \subseteq \mathrm {V}_\kappa $
is generic over
$\mathrm {C} \subseteq \mathrm {V}_\kappa $
is generic over
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
for a the forcing
$(\mathrm {V}_\kappa ,\mathcal {M})$
for a the forcing
![]() $\mathrm {Add}(\kappa ,1)$
and
$\mathrm {Add}(\kappa ,1)$
and
![]() $\mathrm {C}$
is uniformly second-order definable in every model of
$\mathrm {C}$
is uniformly second-order definable in every model of
![]() $\mathsf {KMCC}_k$
which width-extends
$\mathsf {KMCC}_k$
which width-extends
![]() $\mathcal {M}$
. Then we can define, via a second-order formula, a code
$\mathcal {M}$
. Then we can define, via a second-order formula, a code
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
for
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
for
![]() $\mathcal {M}(\mathrm {C})$
in such a way that any model of
$\mathcal {M}(\mathrm {C})$
in such a way that any model of
![]() $\mathsf {KMCC}_k$
which width-extends
$\mathsf {KMCC}_k$
which width-extends
![]() $\mathcal {M}$
will define
$\mathcal {M}$
will define
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
the same.
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
the same.
Proof Sketch
Again we use a definable cofinal map
![]() $f : \kappa \to \alpha $
to define
$f : \kappa \to \alpha $
to define
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
. The difference is, rather than ask about elements of levels of
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
. The difference is, rather than ask about elements of levels of
![]() $\mathrm {L}(\mathrm {V}_\kappa )$
we ask about what conditions in
$\mathrm {L}(\mathrm {V}_\kappa )$
we ask about what conditions in
![]() $\mathrm {C}$
force. Here’s one way you could implement this. Put
$\mathrm {C}$
force. Here’s one way you could implement this. Put
![]() $(i,j,x)$
in
$(i,j,x)$
in
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
if there is a condition
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
if there is a condition
![]() $p \in \mathrm {C}$
which forces that x is an element of the j-th element of
$p \in \mathrm {C}$
which forces that x is an element of the j-th element of
![]() $\mathrm {L}_{f(i)}(\mathrm {V}_\kappa ,\mathrm {C})$
according to the
$\mathrm {L}_{f(i)}(\mathrm {V}_\kappa ,\mathrm {C})$
according to the
![]() $\mathrm {L}(\mathrm {V}_\kappa ,\mathrm {C})$
-least enumeration. Again the forcing lemma lets us do this definition inside
$\mathrm {L}(\mathrm {V}_\kappa ,\mathrm {C})$
-least enumeration. Again the forcing lemma lets us do this definition inside
![]() $\mathcal {M}$
. This definition is uniform across width-extensions because they have the same class well-orders and thus compute
$\mathcal {M}$
. This definition is uniform across width-extensions because they have the same class well-orders and thus compute
![]() $\mathrm {L}(\mathrm {V}_\kappa )$
the same.
$\mathrm {L}(\mathrm {V}_\kappa )$
the same.
It remains to give the definition for
![]() $\mathrm {C}$
. We use the same strategy as before to get a definition absolute for width-extensions of
$\mathrm {C}$
. We use the same strategy as before to get a definition absolute for width-extensions of
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
. From the code
$(\mathrm {V}_\kappa ,\mathcal {M})$
. From the code
![]() $\mathrm {T}_{\mathcal {M}}$
we canonically extract a
$\mathrm {T}_{\mathcal {M}}$
we canonically extract a
![]() $\kappa $
-sequence of dense subclasses of
$\kappa $
-sequence of dense subclasses of
![]() $\mathrm {Add}(\kappa ,1)$
in
$\mathrm {Add}(\kappa ,1)$
in
![]() $\mathcal {M}$
and meet them one at a time. We use the
$\mathcal {M}$
and meet them one at a time. We use the
![]() $\mathrm {HOD}$
-order in
$\mathrm {HOD}$
-order in
![]() $\mathrm {V}_\kappa $
to ensure a canonical choice at each step.
$\mathrm {V}_\kappa $
to ensure a canonical choice at each step.
Lemma 3.2.6. There is a second-order definition for
![]() $\mathrm {C} \subseteq \kappa $
which is Cohen-generic over
$\mathrm {C} \subseteq \kappa $
which is Cohen-generic over
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
so that any model of
$(\mathrm {V}_\kappa ,\mathcal {M})$
so that any model of
![]() $\mathsf {KMCC}_k$
which width-extends
$\mathsf {KMCC}_k$
which width-extends
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
defines
$(\mathrm {V}_\kappa ,\mathcal {M})$
defines
![]() $\mathrm {C}$
the same. Consequently, there is a second-order definition for
$\mathrm {C}$
the same. Consequently, there is a second-order definition for
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
so that all width extensions of
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
so that all width extensions of
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
which satisfy
$(\mathrm {V}_\kappa ,\mathcal {M})$
which satisfy
![]() $\mathsf {KMCC}_k$
will define
$\mathsf {KMCC}_k$
will define
![]() $\mathrm {T}(\mathrm {C})$
the same.
$\mathrm {T}(\mathrm {C})$
the same.
Recall Theorem 2.2.3 that tame class forcing, such as adding a Cohen-generic class of ordinals, preserves
![]() $\mathsf {KMCC}_k$
. Also recall Theorem 2.2.5 that tame class forcing produces width-extensions. So
$\mathsf {KMCC}_k$
. Also recall Theorem 2.2.5 that tame class forcing produces width-extensions. So
![]() $(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
is among the width-extensions of
$(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
is among the width-extensions of
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
subject to the conclusion of the lemma.
$(\mathrm {V}_\kappa ,\mathcal {M})$
subject to the conclusion of the lemma.
We are now in a position to exhibit that
![]() $\Sigma _{k}^1\text {-}\mathsf {CA}$
is not semantically tight. This is analogous to the
$\Sigma _{k}^1\text {-}\mathsf {CA}$
is not semantically tight. This is analogous to the
![]() $\mathsf {GB}$
proof, so we omit most the details.
$\mathsf {GB}$
proof, so we omit most the details.
Theorem 3.2.7. Let
![]() $k \ge 1$
, let
$k \ge 1$
, let
![]() $\kappa $
be inaccessible, and let
$\kappa $
be inaccessible, and let
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathrm {C}$
be defined as above, where we assume
$\mathrm {C}$
be defined as above, where we assume
![]() $\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
. The two models
$\mathrm {V}_\kappa \models \mathrm {V} = \mathrm {HOD}$
. The two models
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
and
$(\mathrm {V}_\kappa ,\mathcal {M})$
and
![]() $(\mathrm {V}_\kappa ,\mathcal {M}(\mathrm {C}))$
of
$(\mathrm {V}_\kappa ,\mathcal {M}(\mathrm {C}))$
of
![]() $\mathsf {KMCC}_k$
are bi-interpretable.
$\mathsf {KMCC}_k$
are bi-interpretable.
Corollary 3.2.8.
![]() $\mathsf {KM}_k$
and
$\mathsf {KM}_k$
and
![]() $\mathsf {KMCC}_k$
are not semantically tight.
$\mathsf {KMCC}_k$
are not semantically tight.
Proof Sketch of Theorem
Interpreting
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
inside the larger model
$(\mathrm {V}_\kappa ,\mathcal {M})$
inside the larger model
![]() $(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
is easy, because
$(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
is easy, because
![]() $\mathcal {M}$
is a definable hyperclass in the larger model. For the other direction, use the code
$\mathcal {M}$
is a definable hyperclass in the larger model. For the other direction, use the code
![]() $\mathrm {T}_{\mathcal {M}}[\mathrm {C}]$
, which is second-order definable over
$\mathrm {T}_{\mathcal {M}}[\mathrm {C}]$
, which is second-order definable over
![]() $(\mathrm {V}_\kappa ,\mathcal {M})$
to give an interpretation, as in the similar direction in the proof of Theorem 3.1.5, interpreting classes in the larger model by the (
$(\mathrm {V}_\kappa ,\mathcal {M})$
to give an interpretation, as in the similar direction in the proof of Theorem 3.1.5, interpreting classes in the larger model by the (
![]() $\mathrm {HOD}$
-least) index of their slice in
$\mathrm {HOD}$
-least) index of their slice in
![]() $\mathrm {T}_{\mathcal {M}}$
.
$\mathrm {T}_{\mathcal {M}}$
.
As remarked after the lemmata,
![]() $(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
and
$(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
and
![]() $(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
compute
$(\mathrm {V}_\kappa ,\mathcal {M}[\mathrm {C}])$
compute
![]() $\mathrm {T}_{\mathcal {M}}$
and
$\mathrm {T}_{\mathcal {M}}$
and
![]() $\mathrm {T}_{\mathcal {M}}[\mathrm {C}]$
the same. This ensures that composing one interpretation with the other gives back (an isomorphic copy of) the model we started out with.
$\mathrm {T}_{\mathcal {M}}[\mathrm {C}]$
the same. This ensures that composing one interpretation with the other gives back (an isomorphic copy of) the model we started out with.
4 Non-tightness in class theory
To obtain the nontightness of the class theories we consider we need a uniform construction, one which applies to any model of a fixed first-order theory. We will strengthen the theories we used to ensure an appropriately modified version of the construction from Section 3 goes through in a more general setting. Two key facts about
![]() $\mathrm {V}_\kappa $
we used were its well-foundedness, ensuring uniqueness of certain constructions, and the regularity of
$\mathrm {V}_\kappa $
we used were its well-foundedness, ensuring uniqueness of certain constructions, and the regularity of
![]() $\kappa $
, ensuring that when we constructed a Cohen generic in
$\kappa $
, ensuring that when we constructed a Cohen generic in
![]() $\kappa $
many steps that the partial constructions were sets in
$\kappa $
many steps that the partial constructions were sets in
![]() $\mathrm {V}_\kappa $
. For our purposes we can replace these non-first-order axiomatizable properties with a strong form of the Replacement schema.
$\mathrm {V}_\kappa $
. For our purposes we can replace these non-first-order axiomatizable properties with a strong form of the Replacement schema.
Definition 4.0.1. Let
![]() $\Phi $
be a collection of formulae in the language of set or class theory. The axiom schema of
$\Phi $
be a collection of formulae in the language of set or class theory. The axiom schema of
![]() $\Phi $
-Replacement consists of the instances of Replacement for all functional
$\Phi $
-Replacement consists of the instances of Replacement for all functional
![]() $\varphi \in \Phi $
, i.e., the axioms
$\varphi \in \Phi $
, i.e., the axioms
allowing parameters, which we suppressed here. Let
![]() $\mathsf {SOR}$
denote Second-Order Replacement, namely
$\mathsf {SOR}$
denote Second-Order Replacement, namely
![]() $\Phi $
-Replacement where
$\Phi $
-Replacement where
![]() $\Phi $
is the collection of all second-order formulae in the language of class theory, allowing class parameters.
$\Phi $
is the collection of all second-order formulae in the language of class theory, allowing class parameters.
It is not difficult to see that
![]() $\mathsf {SOR}$
is consistent, given mild large cardinals. If
$\mathsf {SOR}$
is consistent, given mild large cardinals. If
![]() $\kappa $
is inaccessible then
$\kappa $
is inaccessible then
![]() $(\mathrm {V}_\kappa , \mathcal {X}) \models \mathsf {SOR}$
for any collection
$(\mathrm {V}_\kappa , \mathcal {X}) \models \mathsf {SOR}$
for any collection
![]() $\mathcal {X} \subseteq \mathcal {P}(\mathrm {V}_\kappa )$
of classes over
$\mathcal {X} \subseteq \mathcal {P}(\mathrm {V}_\kappa )$
of classes over
![]() $\mathrm {V}_\kappa $
, by the regularity of
$\mathrm {V}_\kappa $
, by the regularity of
![]() $\kappa $
.
$\kappa $
.
Let’s collect some consequences of
![]() $\mathsf {SOR}$
. These are proved using the same arguments for the first-order versions of the axiom/theorem schemata.
$\mathsf {SOR}$
. These are proved using the same arguments for the first-order versions of the axiom/theorem schemata.
Lemma 4.0.2 (Second-order separation)
Fix
![]() $(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. If
$(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. If
![]() $x \in M$
and
$x \in M$
and
![]() $\varphi (y)$
is any second-order formula, possibly with parameters, then
$\varphi (y)$
is any second-order formula, possibly with parameters, then
![]() $\{ y \in ^M x : (M,\mathcal {X}) \models \varphi (y) \}$
is an element of M.Footnote
15
$\{ y \in ^M x : (M,\mathcal {X}) \models \varphi (y) \}$
is an element of M.Footnote
15
Lemma 4.0.3 (Second-order recursion along
 $\mathrm {Ord}$
)
$\mathrm {Ord}$
)
Fix
![]() $(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Let
$(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Let
![]() $G \subseteq M$
be a second-order definable class function. Then there is a unique definable function F over
$G \subseteq M$
be a second-order definable class function. Then there is a unique definable function F over
![]() $(M, \mathcal {X})$
such that
$(M, \mathcal {X})$
such that
![]() $F(\alpha ) = G(F \upharpoonright \alpha )$
for every
$F(\alpha ) = G(F \upharpoonright \alpha )$
for every
![]() $\alpha \in \mathrm {Ord}^M$
.
$\alpha \in \mathrm {Ord}^M$
.
Lemma 4.0.4 (Second-order recursion along set-like, well-founded relations)
Fix
![]() $(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Let
$(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Let
![]() $G \subseteq M$
be a second-order definable class function and let
$G \subseteq M$
be a second-order definable class function and let
![]() $R \subseteq M$
be a second-order definable, set-like, well-founded relation.Footnote
16
Then there is a unique definable function F over
$R \subseteq M$
be a second-order definable, set-like, well-founded relation.Footnote
16
Then there is a unique definable function F over
![]() $(M, \mathcal {X})$
such that
$(M, \mathcal {X})$
such that
![]() $F(x) = G(F \upharpoonright \operatorname {Ext}_R(x))$
for every
$F(x) = G(F \upharpoonright \operatorname {Ext}_R(x))$
for every
![]() $x \in \operatorname {dom} R$
.
$x \in \operatorname {dom} R$
.
We highlight an immediate corollary we will make repeated use of.
Corollary 4.0.5. Fix
![]() $(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Suppose
$(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Suppose
![]() $F \subseteq M$
is defined by second-order recursion. Then for any
$F \subseteq M$
is defined by second-order recursion. Then for any
![]() $x \in M$
we have that
$x \in M$
we have that
![]() $F(x) \in M$
.
$F(x) \in M$
.
Proof Because
![]() $F(x)$
is definable by second-order Separation.
$F(x)$
is definable by second-order Separation.
Lemma 4.0.6 (Second-order induction)
Fix
![]() $(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Let
$(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Let
![]() $R \subseteq M$
be a second-order definable, set-like, well-founded relation. Suppose X is a second-order definable, inductive subset of the domain of R. Then
$R \subseteq M$
be a second-order definable, set-like, well-founded relation. Suppose X is a second-order definable, inductive subset of the domain of R. Then
![]() $X = \operatorname {dom} R$
.
$X = \operatorname {dom} R$
.
An instance of this is especially relevant to our purposes.
Corollary 4.0.7. Over
![]() $\mathsf {GB}$
,
$\mathsf {GB}$
,
![]() $\mathsf {SOR}$
proves the single sentence that asserts for every
$\mathsf {SOR}$
proves the single sentence that asserts for every
![]() $k \in \omega $
there is a
$k \in \omega $
there is a
![]() $\Sigma _k$
satisfaction predicate.
$\Sigma _k$
satisfaction predicate.
Proof It is easy to see that the subset of
![]() $\omega $
consisting of the k for which a
$\omega $
consisting of the k for which a
![]() $\Sigma _k$
satisfaction predicate exists is inductive.
$\Sigma _k$
satisfaction predicate exists is inductive.
Just
![]() $\mathsf {GB}$
alone proves the existence of the
$\mathsf {GB}$
alone proves the existence of the
![]() $\Sigma _k$
satisfaction predicate for every standard k, by an induction in the metatheory. The point is, with
$\Sigma _k$
satisfaction predicate for every standard k, by an induction in the metatheory. The point is, with
![]() $\mathsf {SOR}$
the quantification over k is not in the metatheory and we get
$\mathsf {SOR}$
the quantification over k is not in the metatheory and we get
![]() $\Sigma _k$
satisfaction predicates even for nonstandard k. The connoisseur of nonstandard models knows that
$\Sigma _k$
satisfaction predicates even for nonstandard k. The connoisseur of nonstandard models knows that
![]() $\omega $
-nonstandard models may fail to admit any
$\omega $
-nonstandard models may fail to admit any
![]() $\Sigma _k$
satisfaction predicate for nonstandard k.Footnote
17
Second-Order Replacement rules these models out from consideration.
$\Sigma _k$
satisfaction predicate for nonstandard k.Footnote
17
Second-Order Replacement rules these models out from consideration.
As an aside, we remark that
![]() $\mathsf {GB} + \mathsf {SOR}$
exceeds
$\mathsf {GB} + \mathsf {SOR}$
exceeds
![]() $\mathsf {GB}$
in consistency strength.
$\mathsf {GB}$
in consistency strength.
Proposition 4.0.8.
![]() $\mathsf {GB} + \mathsf {SOR}$
proves the consistency of
$\mathsf {GB} + \mathsf {SOR}$
proves the consistency of
![]() $\mathsf {GB}$
.
$\mathsf {GB}$
.
Proof Sketch
Work internally to a model of
![]() $\mathsf {GB} + \mathsf {SOR}$
. By second-order Separation form the set of (parameter-free) first-order truths of the universe of sets. By induction this truth set contains every instance of Replacement and Separation. And it must be consistent, so we have constructed a consistent extension of
$\mathsf {GB} + \mathsf {SOR}$
. By second-order Separation form the set of (parameter-free) first-order truths of the universe of sets. By induction this truth set contains every instance of Replacement and Separation. And it must be consistent, so we have constructed a consistent extension of
![]() $\mathsf {ZFC}$
, whence we get the consistency of
$\mathsf {ZFC}$
, whence we get the consistency of
![]() $\mathsf {GB}$
.
$\mathsf {GB}$
.
On the other hand,
![]() $\mathsf {SOR}$
says very little about what classes exist.
$\mathsf {SOR}$
says very little about what classes exist.
Lemma 4.0.9. Let
![]() $(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Suppose
$(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Suppose
![]() $\mathcal {Y} \subseteq \mathcal {X}$
is definable over
$\mathcal {Y} \subseteq \mathcal {X}$
is definable over
![]() $(M,\mathcal {X})$
by a second-order formula, possibly using parameters. Then
$(M,\mathcal {X})$
by a second-order formula, possibly using parameters. Then
![]() $(M,\mathcal {Y}) \models \mathsf {SOR}$
.
$(M,\mathcal {Y}) \models \mathsf {SOR}$
.
Proof Consider an instance
![]() $\psi $
of
$\psi $
of
![]() $\mathsf {SOR}$
. Let
$\mathsf {SOR}$
. Let
![]() $\psi ^{\mathcal {Y}}$
be the relativization of
$\psi ^{\mathcal {Y}}$
be the relativization of
![]() $\psi $
so that class quantifiers only quantify over elements of
$\psi $
so that class quantifiers only quantify over elements of
![]() $\mathcal {Y}$
, using that
$\mathcal {Y}$
, using that
![]() $\mathcal {Y}$
is definable. (Set quantifiers are unchanged.) By
$\mathcal {Y}$
is definable. (Set quantifiers are unchanged.) By
![]() $\mathsf {SOR}$
we get that
$\mathsf {SOR}$
we get that
![]() $(M,\mathcal {X}) \models \psi ^{\mathcal {Y}}$
. Hence
$(M,\mathcal {X}) \models \psi ^{\mathcal {Y}}$
. Hence
![]() $(M,\mathcal {Y}) \models \psi $
.
$(M,\mathcal {Y}) \models \psi $
.
In particular, by similar logic as to how we defined
![]() $\operatorname {Def}(\mathrm {V}_\kappa )$
in the previous section, we will get that any model of
$\operatorname {Def}(\mathrm {V}_\kappa )$
in the previous section, we will get that any model of
![]() $\mathsf {GB}$
can define what internally looks like the definable classes. This gives a model of
$\mathsf {GB}$
can define what internally looks like the definable classes. This gives a model of
![]() $\mathsf {GB} + \mathsf {SOR}$
with a weak second-order theory, not even able to prove the existence of a satisfaction predicate which measures all first-order formulae. Such a model will fail to satisfy even
$\mathsf {GB} + \mathsf {SOR}$
with a weak second-order theory, not even able to prove the existence of a satisfaction predicate which measures all first-order formulae. Such a model will fail to satisfy even
![]() $\Pi _1^1\text {-}\mathsf {CA}$
.
$\Pi _1^1\text {-}\mathsf {CA}$
.
We close this section with the fact that forcing preserves
![]() $\mathsf {SOR}$
.
$\mathsf {SOR}$
.
Lemma 4.0.10. Suppose
![]() $(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Then, any forcing extension of
$(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR}$
. Then, any forcing extension of
![]() $(M,\mathcal {X})$
by a tame,
$(M,\mathcal {X})$
by a tame,
![]() $\mathord {<}\mathrm {Ord}$
-closed forcing in
$\mathord {<}\mathrm {Ord}$
-closed forcing in
![]() $\mathcal {X}$
will satisfy
$\mathcal {X}$
will satisfy
![]() $\mathsf {SOR}$
.
$\mathsf {SOR}$
.
Proof Let
![]() $(M,\mathcal {X}[G])$
denote the forcing extension—the sets are the same by
$(M,\mathcal {X}[G])$
denote the forcing extension—the sets are the same by
![]() $\mathord {<}\mathrm {Ord}$
-closure—and suppose toward a contradiction that it fails to satisfy
$\mathord {<}\mathrm {Ord}$
-closure—and suppose toward a contradiction that it fails to satisfy
![]() $\mathsf {SOR}$
. Let
$\mathsf {SOR}$
. Let
![]() $\varphi (x,y)$
be an instance of
$\varphi (x,y)$
be an instance of
![]() $\mathsf {SOR}$
which fails in this extension; that is,
$\mathsf {SOR}$
which fails in this extension; that is,
![]() $(M,\mathcal {X}[G])$
has a set a so that for all
$(M,\mathcal {X}[G])$
has a set a so that for all
![]() $x \in a$
there is unique y so that
$x \in a$
there is unique y so that
![]() $\varphi (x,y)$
but there is no set containing all such y. This is forced by some condition
$\varphi (x,y)$
but there is no set containing all such y. This is forced by some condition
![]() $p \in G$
. By
$p \in G$
. By
![]() $\mathord {<}\mathrm {Ord}$
-closure we may moreover assume that p decides the identity of each of these witnesses; there are
$\mathord {<}\mathrm {Ord}$
-closure we may moreover assume that p decides the identity of each of these witnesses; there are
![]() $\left \lvert a \right \rvert < \mathrm {Ord}$
many names to decide, so by closure we have enough space to continually extend to decide each of them. And they are decided to be equal to some check name
$\left \lvert a \right \rvert < \mathrm {Ord}$
many names to decide, so by closure we have enough space to continually extend to decide each of them. And they are decided to be equal to some check name
![]() $\check y$
, since no sets are added. But then
$\check y$
, since no sets are added. But then
![]() $(M,\mathcal {X})$
satisfies that there is a set a so that for all
$(M,\mathcal {X})$
satisfies that there is a set a so that for all
![]() $x \in a$
there is a unique set y so that
$x \in a$
there is a unique set y so that
![]() $p \Vdash \varphi (\check x,\check y)$
, with no set b containing all such y. This is a failure of
$p \Vdash \varphi (\check x,\check y)$
, with no set b containing all such y. This is a failure of
![]() $\mathsf {SOR}$
in the ground model, contrary to the assumptions of the lemma.
$\mathsf {SOR}$
in the ground model, contrary to the assumptions of the lemma.
4.1 Non-tightness of
 $\mathsf {GB}$
$\mathsf {GB}$
All results in this section concern models of
![]() $\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
, and the reader is warned we will not make this assumption explicit in every single definition and lemma. Many results do not need the full strength of this assumption, but we leave it to the interested reader to identify the minimal assumptions for each result.
$\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
, and the reader is warned we will not make this assumption explicit in every single definition and lemma. Many results do not need the full strength of this assumption, but we leave it to the interested reader to identify the minimal assumptions for each result.
We start this section by considering truth and definability. We take some care to make it clear everything works in the
![]() $\omega $
-nonstandard case. All definitions that follow take place in the context of a fixed model of
$\omega $
-nonstandard case. All definitions that follow take place in the context of a fixed model of
![]() $\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
.
$\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
.
Definition 4.1.1. A partial satisfaction predicate is a class S of (first-order) formulae
![]() $\varphi [\vec a]$
equipped with set parameters assigned to all free variables so that the domain of S is closed under subformulae and S satisfies the Tarskian recursion on its domain. If the domain of S is all
$\varphi [\vec a]$
equipped with set parameters assigned to all free variables so that the domain of S is closed under subformulae and S satisfies the Tarskian recursion on its domain. If the domain of S is all
![]() $\Sigma _k$
formulae, for
$\Sigma _k$
formulae, for
![]() $k \in \omega $
, we call S the
$k \in \omega $
, we call S the
![]() $\Sigma _k$
satisfaction predicate.
$\Sigma _k$
satisfaction predicate.
Our use of the definite article in that last sentence is justified by the following observation.
Proposition 4.1.2. Any two partial satisfaction classes agree on their common domain.
Proof By Elementary Comprehension form the class of locations where they disagree. If nonempty there must be a minimal location
![]() $\varphi [\vec a]$
of disagreement. But since they agree on subformulae of
$\varphi [\vec a]$
of disagreement. But since they agree on subformulae of
![]() $\varphi [\vec a]$
and they both satisfy the Tarskian recursion they must agree on the truth of
$\varphi [\vec a]$
and they both satisfy the Tarskian recursion they must agree on the truth of
![]() $\varphi [\vec a]$
.
$\varphi [\vec a]$
.
Definition 4.1.3. Define
![]() $\mathrm {T}$
to be the union of all partial satisfaction predicate. Write
$\mathrm {T}$
to be the union of all partial satisfaction predicate. Write
![]() $\mathrm {T}_k$
for the
$\mathrm {T}_k$
for the
![]() $\Sigma _k$
satisfaction predicate.
$\Sigma _k$
satisfaction predicate.
It follows from earlier remarks that
![]() $\mathsf {SOR}$
implies
$\mathsf {SOR}$
implies
![]() $\mathrm {T}$
is the full satisfaction predicate, the unique satisfaction predicate that measures the truth of all formulae.Footnote
18
$\mathrm {T}$
is the full satisfaction predicate, the unique satisfaction predicate that measures the truth of all formulae.Footnote
18
A notion of satisfaction carries a notion of definability. Let
![]() $\mathcal {D}$
be the (second-order definable) hyperclass of all
$\mathcal {D}$
be the (second-order definable) hyperclass of all
![]() $\mathrm {T}$
-definable classes. That is,
$\mathrm {T}$
-definable classes. That is,
![]() $X \in \mathcal {D}$
if and only if there is
$X \in \mathcal {D}$
if and only if there is
![]() $\varphi [x,\vec a]$
so that
$\varphi [x,\vec a]$
so that
![]() $X = \{ x : \varphi [x,\vec a] \in \mathrm {T}\}$
. As in the
$X = \{ x : \varphi [x,\vec a] \in \mathrm {T}\}$
. As in the
![]() $\mathrm {V}_\kappa $
case, with minor reshuffling of indexing
$\mathrm {V}_\kappa $
case, with minor reshuffling of indexing
![]() $\mathrm {T}$
gives a code for
$\mathrm {T}$
gives a code for
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Definition 4.1.4. We write
![]() $\mathrm {Class} = \operatorname {Def}(V)$
to denote the axiom asserting that every class is in
$\mathrm {Class} = \operatorname {Def}(V)$
to denote the axiom asserting that every class is in
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 4.1.5. Consider a model
![]() $(M,\mathcal {X})$
of
$(M,\mathcal {X})$
of
![]() $\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
. Then
$\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
. Then
![]() $\mathcal {D}^{\mathcal {X}} \subseteq \mathcal {X}$
and
$\mathcal {D}^{\mathcal {X}} \subseteq \mathcal {X}$
and
![]() $(M,\mathcal {D}^{\mathcal {X}}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
.
$(M,\mathcal {D}^{\mathcal {X}}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
.
Proof For the first part, we note that X is
![]() $\mathrm {T}$
-definable if, and only if, X is
$\mathrm {T}$
-definable if, and only if, X is
![]() $\Sigma _k$
-definable for some
$\Sigma _k$
-definable for some
![]() $k \in \omega ^M$
. By
$k \in \omega ^M$
. By
![]() $\mathsf {SOR}$
, for each k the
$\mathsf {SOR}$
, for each k the
![]() $\Sigma _k$
satisfaction predicate is in
$\Sigma _k$
satisfaction predicate is in
![]() $\mathcal {X}$
. So from First-Order Comprehension we obtain
$\mathcal {X}$
. So from First-Order Comprehension we obtain
![]() $X \in \mathcal {X}$
.
$X \in \mathcal {X}$
.
For the second part: Extensionality is trivially obtained and Replacement holds because it holds in the larger
![]() $\mathcal {X}$
. For First-Order Comprehension, fix
$\mathcal {X}$
. For First-Order Comprehension, fix
![]() $A \in \mathcal {D}^{\mathcal {X}}$
and assume B is externally definable from A via a
$A \in \mathcal {D}^{\mathcal {X}}$
and assume B is externally definable from A via a
![]() $\Sigma _\ell $
-formula with set parameters, i.e., for standard
$\Sigma _\ell $
-formula with set parameters, i.e., for standard
![]() $\ell $
. Because A is
$\ell $
. Because A is
![]() $\mathrm {T}$
-definable that means that A is
$\mathrm {T}$
-definable that means that A is
![]() $\Sigma _k$
-definable for some level k in
$\Sigma _k$
-definable for some level k in
![]() $\omega ^M$
. But then B is
$\omega ^M$
. But then B is
![]() $\Sigma _{k+\ell }$
-definable, whence B is
$\Sigma _{k+\ell }$
-definable, whence B is
![]() $\mathrm {T}$
-definable. Finally, that
$\mathrm {T}$
-definable. Finally, that
![]() $(M,\mathcal {D}^{\mathcal {X}})$
satisfies
$(M,\mathcal {D}^{\mathcal {X}})$
satisfies
![]() $\mathsf {SOR}$
is Lemma 4.0.9 and that it satisfies
$\mathsf {SOR}$
is Lemma 4.0.9 and that it satisfies
![]() $\mathrm {V} = \mathrm {HOD}$
is because
$\mathrm {V} = \mathrm {HOD}$
is because
![]() $\mathrm {V} = \mathrm {HOD}$
only quantifies over sets.
$\mathrm {V} = \mathrm {HOD}$
only quantifies over sets.
Lemma 4.1.6. The definition of
![]() $\mathcal {D}$
is absolute between models with the same sets and the same
$\mathcal {D}$
is absolute between models with the same sets and the same
![]() $\mathrm {T}$
. That is, if
$\mathrm {T}$
. That is, if
![]() $(M,\mathcal {X})$
and
$(M,\mathcal {X})$
and
![]() $(M,\mathcal {Y})$
are models where
$(M,\mathcal {Y})$
are models where
![]() $\mathrm {T}^{\mathcal {X}} = \mathrm {T}^{\mathcal {Y}}$
then
$\mathrm {T}^{\mathcal {X}} = \mathrm {T}^{\mathcal {Y}}$
then
![]() $\mathcal {D}^{\mathcal {X}} = \mathcal {D}^{\mathcal {Y}}$
.
$\mathcal {D}^{\mathcal {X}} = \mathcal {D}^{\mathcal {Y}}$
.
Proof Just observe that the definition of
![]() $\mathcal {D}$
from the parameter
$\mathcal {D}$
from the parameter
![]() $\mathrm {T}$
only quantifies over sets.
$\mathrm {T}$
only quantifies over sets.
Lemma 4.1.7. Moving to
![]() $\mathcal {D}$
preserves the satisfaction predicate. In symbols:
$\mathcal {D}$
preserves the satisfaction predicate. In symbols:
![]() $\mathrm {T}^{\mathcal {D}} = \mathrm {T}$
.
$\mathrm {T}^{\mathcal {D}} = \mathrm {T}$
.
Proof Because the
![]() $\Sigma _k$
satisfaction predicate is
$\Sigma _k$
satisfaction predicate is
![]() $\Sigma _{k+1}$
-definable.
$\Sigma _{k+1}$
-definable.
Altogether, we have that
![]() $\mathcal {D}$
thinks it is the minimum model of
$\mathcal {D}$
thinks it is the minimum model of
![]() $\mathsf {GB}$
.
$\mathsf {GB}$
.
Corollary 4.1.8. The
![]() $\mathcal {D}$
operator is idempotent. That is, for any
$\mathcal {D}$
operator is idempotent. That is, for any
![]() $(M,\mathcal {X}) \models \mathsf {GB}$
we have that
$(M,\mathcal {X}) \models \mathsf {GB}$
we have that
![]() $\mathcal {D}^{\mathcal {D}^{\mathcal {X}}} = \mathcal {D}^{\mathcal {X}}$
. Consequently,
$\mathcal {D}^{\mathcal {D}^{\mathcal {X}}} = \mathcal {D}^{\mathcal {X}}$
. Consequently,
![]() $(M,\mathcal {D}^{\mathcal {X}})$
satisfies
$(M,\mathcal {D}^{\mathcal {X}})$
satisfies
![]() $\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V)$
.
$\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V)$
.
Corollary 4.1.9. If
![]() $(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V)$
, then
$(M, \mathcal {X}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V)$
, then
![]() $\mathcal {X} = \mathcal {D}^{\mathcal {X}}$
.
$\mathcal {X} = \mathcal {D}^{\mathcal {X}}$
.
These definitions and results about satisfaction/definability can be relativized to a class parameter. If this parameter is an element of
![]() $\mathcal {X}$
then the proofs are near identical. If the parameter is a second-order definable Cohen generic then we need a slight change. As in the proof of Lemma 3.1.3, the change is to ask about what is forced. We state the relativized results only for the Cohen generic case, and omit any proofs as they are the same modulo this small change.
$\mathcal {X}$
then the proofs are near identical. If the parameter is a second-order definable Cohen generic then we need a slight change. As in the proof of Lemma 3.1.3, the change is to ask about what is forced. We state the relativized results only for the Cohen generic case, and omit any proofs as they are the same modulo this small change.
Lemma 4.1.10. Fix
![]() $(M,\mathcal {X}) \models \mathsf {GB}$
and suppose
$(M,\mathcal {X}) \models \mathsf {GB}$
and suppose
![]() $\mathrm {C} \subseteq M$
is generic over
$\mathrm {C} \subseteq M$
is generic over
![]() $\mathcal {D}^{\mathcal {X}}$
for the forcing
$\mathcal {D}^{\mathcal {X}}$
for the forcing
![]() $\mathrm {Add}(\mathrm {Ord},1)$
. Then
$\mathrm {Add}(\mathrm {Ord},1)$
. Then
![]() $\mathrm {C} \in \mathcal {D}(\mathrm {C})^{\mathcal {X}}$
and
$\mathrm {C} \in \mathcal {D}(\mathrm {C})^{\mathcal {X}}$
and
![]() $(M,\mathcal {D}(\mathrm {C})^{\mathcal {X}}) \models \mathsf {GB}$
. Moreover, if
$(M,\mathcal {D}(\mathrm {C})^{\mathcal {X}}) \models \mathsf {GB}$
. Moreover, if
![]() $\mathrm {C}$
is uniformly definable over models with the same sets and the same
$\mathrm {C}$
is uniformly definable over models with the same sets and the same
![]() $\mathrm {T}$
, then the definitions of
$\mathrm {T}$
, then the definitions of
![]() $\mathrm {T}(\mathrm {C})$
and
$\mathrm {T}(\mathrm {C})$
and
![]() $\mathcal {D}(\mathrm {C})$
are absolute between these models.
$\mathcal {D}(\mathrm {C})$
are absolute between these models.
Lemma 4.1.11. For any
![]() $(M,\mathcal {X}) \models \mathsf {GB}$
and any Cohen-generic
$(M,\mathcal {X}) \models \mathsf {GB}$
and any Cohen-generic
![]() $\mathrm {C}$
, we have that
$\mathrm {C}$
, we have that
![]() $\mathcal {D}(\mathrm {C})^{\mathcal {D}(\mathrm {C})^{\mathcal {X}}} = \mathcal {D}(\mathrm {C})^{\mathcal {X}}$
.
$\mathcal {D}(\mathrm {C})^{\mathcal {D}(\mathrm {C})^{\mathcal {X}}} = \mathcal {D}(\mathrm {C})^{\mathcal {X}}$
.
Corollary 4.1.12. Fix
![]() $(M,\mathcal {X}) \models \mathsf {GB}$
and fix a Cohen-generic
$(M,\mathcal {X}) \models \mathsf {GB}$
and fix a Cohen-generic
![]() $\mathrm {C}$
. Then
$\mathrm {C}$
. Then
![]() $(M,\mathcal {D}(\mathrm {C})^{\mathcal {X}}) \models \mathsf {GB} + \mathrm {Class} = \operatorname {Def}(V; \mathrm {C})$
. Note that this can be expressed as a single second-order assertion, using the parameter
$(M,\mathcal {D}(\mathrm {C})^{\mathcal {X}}) \models \mathsf {GB} + \mathrm {Class} = \operatorname {Def}(V; \mathrm {C})$
. Note that this can be expressed as a single second-order assertion, using the parameter
![]() $\mathrm {C}$
.
$\mathrm {C}$
.
Corollary 4.1.13. If
![]() $(M, \mathcal {X}) \models \mathsf {GB} + Class = \operatorname {Def}(V; \mathrm {C})$
where
$(M, \mathcal {X}) \models \mathsf {GB} + Class = \operatorname {Def}(V; \mathrm {C})$
where
![]() $\mathrm {C}$
is a Cohen-generic over
$\mathrm {C}$
is a Cohen-generic over
![]() $(M,\mathcal {D}^{\mathcal {X}})$
, then
$(M,\mathcal {D}^{\mathcal {X}})$
, then
![]() $\mathcal {X} = \mathcal {D}(\mathrm {C})^{\mathcal {X}}$
.
$\mathcal {X} = \mathcal {D}(\mathrm {C})^{\mathcal {X}}$
.
Now we turn our attention to the definition of the Cohen generic
![]() $\mathrm {C}$
we use in our construction.
$\mathrm {C}$
we use in our construction.
Lemma 4.1.14. Work over
![]() $(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
. Over this model there is second-order definable
$(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
. Over this model there is second-order definable
![]() $\mathrm {C} \subseteq M$
which is generic for
$\mathrm {C} \subseteq M$
which is generic for
![]() $\mathrm {Add}(\mathrm {Ord},1)^M$
over
$\mathrm {Add}(\mathrm {Ord},1)^M$
over
![]() $(M,\mathcal {D}^{\mathcal {X}})$
. Moreover,
$(M,\mathcal {D}^{\mathcal {X}})$
. Moreover,
![]() $\mathrm {C}$
and
$\mathrm {C}$
and
![]() $\mathrm {T}(\mathrm {C})$
are absolute to any
$\mathrm {T}(\mathrm {C})$
are absolute to any
![]() $(M,\mathcal {Y}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
for which
$(M,\mathcal {Y}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
for which
![]() $\mathrm {T}^{\mathcal {Y}} = \mathrm {T}^{\mathcal {X}}$
.
$\mathrm {T}^{\mathcal {Y}} = \mathrm {T}^{\mathcal {X}}$
.
Proof As in Lemma 3.1.4, we define the class
![]() $D \subset \mathrm {Ord} \times \mathrm {Add}(\mathrm {Ord}, 1)$
such that the slices
$D \subset \mathrm {Ord} \times \mathrm {Add}(\mathrm {Ord}, 1)$
such that the slices
![]() $(D)_i$
are all the
$(D)_i$
are all the
![]() $\mathrm {T}$
-definable dense subclass of
$\mathrm {T}$
-definable dense subclass of
![]() $\mathrm {Add}(\mathrm {Ord}, 1)$
. The order in D is obtained from the
$\mathrm {Add}(\mathrm {Ord}, 1)$
. The order in D is obtained from the
![]() $\mathrm {HOD}$
-order in M. We also use the
$\mathrm {HOD}$
-order in M. We also use the
![]() $\mathrm {HOD}$
-order to recursively build the sequence of increasingly stronger forcing condition
$\mathrm {HOD}$
-order to recursively build the sequence of increasingly stronger forcing condition
![]() ${\left \langle p_\xi : \xi \in \mathrm {Ord} \right \rangle }$
such that
${\left \langle p_\xi : \xi \in \mathrm {Ord} \right \rangle }$
such that
![]() $p_\xi \in (D)_\xi $
. This is where we use
$p_\xi \in (D)_\xi $
. This is where we use
![]() $\mathsf {SOR}$
: This sequence is defined by transfinite recursion using a second-order definition (because we need a second-order definition to define
$\mathsf {SOR}$
: This sequence is defined by transfinite recursion using a second-order definition (because we need a second-order definition to define
![]() $\mathrm {T}$
to thereby define D). By Lemma 4.0.3 this recursion succeeds and the initial segments of the sequences are sets in M.
$\mathrm {T}$
to thereby define D). By Lemma 4.0.3 this recursion succeeds and the initial segments of the sequences are sets in M.
What remains in the proof is precisely the same as in the proof of Lemma 3.1.4. We omit repeating it.
A consequence of Lemma 4.0.10 is that the extension by
![]() $\mathrm {C}$
will satisfy
$\mathrm {C}$
will satisfy
![]() $\mathsf {SOR}$
. To check that the lemma we just proved includes this extension itself we simply need to check that it defines
$\mathsf {SOR}$
. To check that the lemma we just proved includes this extension itself we simply need to check that it defines
![]() $\mathrm {T}$
the same as its ground model. Fortunately this is easy.
$\mathrm {T}$
the same as its ground model. Fortunately this is easy.
Lemma 4.1.15. Let
![]() $(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
. Then any extension of
$(M,\mathcal {X}) \models \mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD}$
. Then any extension of
![]() $(M,\mathcal {X})$
by a tame forcing in
$(M,\mathcal {X})$
by a tame forcing in
![]() $\mathcal {X}$
which does not add sets will define
$\mathcal {X}$
which does not add sets will define
![]() $\mathrm {T}$
the same as
$\mathrm {T}$
the same as
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Proof Let
![]() $(M,\mathcal {X}[G])$
denote the forcing extension. It satisfies
$(M,\mathcal {X}[G])$
denote the forcing extension. It satisfies
![]() $\mathsf {GB}$
, so it thinks that
$\mathsf {GB}$
, so it thinks that
![]() $\Sigma _k$
satisfaction predicates are unique. Since
$\Sigma _k$
satisfaction predicates are unique. Since
![]() $\mathcal {X}[G]$
contains all of
$\mathcal {X}[G]$
contains all of
![]() $\mathcal {X}$
, it thus agrees with
$\mathcal {X}$
, it thus agrees with
![]() $\mathcal {X}$
as to what class is the
$\mathcal {X}$
as to what class is the
![]() $\Sigma _k$
satisfaction predicate for all k, even nonstandard. So they define
$\Sigma _k$
satisfaction predicate for all k, even nonstandard. So they define
![]() $\mathrm {T}$
the same.
$\mathrm {T}$
the same.
Finally we are in a position to prove that
![]() $\mathsf {GB}$
is not tight.
$\mathsf {GB}$
is not tight.
Theorem 4.1.16. Consider the following two theories.
-
• D is the theory consisting of
 $\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V)$
.
$\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V)$
. -
• U is the theory consisting of
 $\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V; \mathrm {C})$
where
$\mathsf {GB} + \mathsf {SOR} + \mathrm {V} = \mathrm {HOD} + \mathrm {Class} = \operatorname {Def}(V; \mathrm {C})$
where
 $\mathrm {C}$
is the Cohen generic over
$\mathrm {C}$
is the Cohen generic over
 $\mathcal {D}$
built up according to Lemma 4.1.14.
$\mathcal {D}$
built up according to Lemma 4.1.14.
The theories D and U are bi-interpretable, via interpretations that fix the sets of the models.
Corollary 4.1.17.
![]() $\mathsf {GB}$
and
$\mathsf {GB}$
and
![]() $\mathsf {GB} + \mathsf {SOR}$
are not tight.
$\mathsf {GB} + \mathsf {SOR}$
are not tight.
Proof Sketch of Theorem
We use the same interpretations
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
from Theorem 3.1.5.
$\mathcal {J}$
from Theorem 3.1.5.
First we interpret D in U via
![]() $\mathcal {I}$
, whose domain is
$\mathcal {I}$
, whose domain is
![]() $\mathcal {D}$
. This is expressible because
$\mathcal {D}$
. This is expressible because
![]() $\mathcal {D}$
is a definable hyperclass. As before,
$\mathcal {D}$
is a definable hyperclass. As before,
![]() $\mathcal {I}$
is the identity on its domain and
$\mathcal {I}$
is the identity on its domain and
![]() $\in ^{\mathcal {I}}$
is
$\in ^{\mathcal {I}}$
is
![]() $\in $
. The lemmata about
$\in $
. The lemmata about
![]() $\mathcal {D}$
then give that this is an interpretation of D in U.
$\mathcal {D}$
then give that this is an interpretation of D in U.
For the other direction let us work in an arbitrary model
![]() $(M, \mathcal {X}) \models D$
. For the sets of the interpreted model we will take all of
$(M, \mathcal {X}) \models D$
. For the sets of the interpreted model we will take all of
![]() $\{0\} \times M$
and for the classes we will take a subset of
$\{0\} \times M$
and for the classes we will take a subset of
![]() $\{1\} \times \mathrm {Ord}.$
Specifically,
$\{1\} \times \mathrm {Ord}.$
Specifically,
![]() $(1,\xi )$
is in the domain of
$(1,\xi )$
is in the domain of
![]() $\mathcal {J}$
just in case
$\mathcal {J}$
just in case
![]() $(\mathrm {T}(\mathrm {C}))_\xi \ne (\mathrm {T}(\mathrm {C}))_\eta $
for all
$(\mathrm {T}(\mathrm {C}))_\xi \ne (\mathrm {T}(\mathrm {C}))_\eta $
for all
![]() $\eta < \xi $
, where the subscripts refer to the rank of the indices in the canonical global well-order. For sets,
$\eta < \xi $
, where the subscripts refer to the rank of the indices in the canonical global well-order. For sets,
![]() $(0,x) \in ^{\mathcal {J}} (0,y)$
if and only if
$(0,x) \in ^{\mathcal {J}} (0,y)$
if and only if
![]() $x \in y$
. For set-class membership,
$x \in y$
. For set-class membership,
![]() $(0,x) \in ^{\mathcal {J}} (1,\eta )$
if and only if
$(0,x) \in ^{\mathcal {J}} (1,\eta )$
if and only if
![]() $x \in (\mathrm {T}(\mathrm {C}))_\eta $
. In effect, the interpretation is that each class in the extension is interpreted as (the index of) the first formula which defines it. The lemmata about
$x \in (\mathrm {T}(\mathrm {C}))_\eta $
. In effect, the interpretation is that each class in the extension is interpreted as (the index of) the first formula which defines it. The lemmata about
![]() $\mathrm {C}$
imply that this is an interpretation of U in D.
$\mathrm {C}$
imply that this is an interpretation of U in D.
That these interpretations compose to give definable bijections is the same argument as in Theorem 3.1.5.
4.2 Non-tightness of
 $\mathsf {KMCC}_k$
$\mathsf {KMCC}_k$
Our work here is to show that the construction in Section 3.2 can be made to work uniformly, instead of working only over a fixed transitive model. As before, it will be convenient to work with the unrolled model of
![]() $\mathsf {ZFC}^-_{\mathrm {I},k}$
as described in Section 2.1. We will use
$\mathsf {ZFC}^-_{\mathrm {I},k}$
as described in Section 2.1. We will use
![]() $\mathrm {Class} = \mathrm {L}$
to mean that every class is (second-order) constructible. More precisely,
$\mathrm {Class} = \mathrm {L}$
to mean that every class is (second-order) constructible. More precisely,
![]() $\mathrm {Class} = \mathrm {L}$
expresses the translation of
$\mathrm {Class} = \mathrm {L}$
expresses the translation of
![]() $\mathrm {V} = \mathrm {L}$
in the unrolled model. Note that
$\mathrm {V} = \mathrm {L}$
in the unrolled model. Note that
![]() $\mathrm {Class} = \mathrm {L}$
implies
$\mathrm {Class} = \mathrm {L}$
implies
![]() $\mathrm {V} = \mathrm {L}$
.Footnote
19
$\mathrm {V} = \mathrm {L}$
.Footnote
19
Before we describe our construction, let us recall the construction in the transitive context. A transitive model of
![]() $\mathsf {ZFC}^-_{\mathrm {I},k} + \mathrm {V} = \mathrm {L}$
is of the form
$\mathsf {ZFC}^-_{\mathrm {I},k} + \mathrm {V} = \mathrm {L}$
is of the form
![]() $\mathrm {L}_\alpha $
and thinks there is a largest cardinal, call it
$\mathrm {L}_\alpha $
and thinks there is a largest cardinal, call it
![]() $\kappa $
, and it is inaccessible. This
$\kappa $
, and it is inaccessible. This
![]() $\mathrm {L}_\alpha $
is bi-interpretable with a model of the form
$\mathrm {L}_\alpha $
is bi-interpretable with a model of the form
![]() $(\mathrm {L}_\kappa , \mathcal {M}) \models \mathsf {KMCC}_k$
. There is a least
$(\mathrm {L}_\kappa , \mathcal {M}) \models \mathsf {KMCC}_k$
. There is a least
![]() $\alpha $
which gives such a model of
$\alpha $
which gives such a model of
![]() $\mathsf {KMCC}_k$
with
$\mathsf {KMCC}_k$
with
![]() $\mathrm {L}_\kappa $
as the sets. It can be characterized as the smallest
$\mathrm {L}_\kappa $
as the sets. It can be characterized as the smallest
![]() $\alpha> \kappa $
which satisfies
$\alpha> \kappa $
which satisfies
![]() $\Sigma _k$
-Replacement.
$\Sigma _k$
-Replacement.
In the transitive setting, we used that such
![]() $\alpha $
must admit some
$\alpha $
must admit some
![]() $\Sigma _{k+1}$
-definable cofinal map
$\Sigma _{k+1}$
-definable cofinal map
![]() $\kappa \to \alpha $
. But if we are to have a uniform construction then we must have a single definition for a cofinal map across all models, and it must be sufficiently absolute to achieve the nontightness of
$\kappa \to \alpha $
. But if we are to have a uniform construction then we must have a single definition for a cofinal map across all models, and it must be sufficiently absolute to achieve the nontightness of
![]() $\mathsf {KMCC}_k$
. The basic idea is, we successively close off under taking witnesses for instances of
$\mathsf {KMCC}_k$
. The basic idea is, we successively close off under taking witnesses for instances of
![]() $\Sigma _k$
-Replacement for more and more inputs. For this we will make use of some fine structural tools.
$\Sigma _k$
-Replacement for more and more inputs. For this we will make use of some fine structural tools.
Briefly: Jensen—e.g., in [Reference Jensen22]—gave a precise analysis of the structure of
![]() $\mathrm {L}$
as built up using rudimentary functions. He considers an alternate hierarchy, the
$\mathrm {L}$
as built up using rudimentary functions. He considers an alternate hierarchy, the
![]() $\mathrm {J}$
hierarchy, to build up
$\mathrm {J}$
hierarchy, to build up
![]() $\mathrm {L}$
. But the
$\mathrm {L}$
. But the
![]() $\mathrm {J}$
and
$\mathrm {J}$
and
![]() $\mathrm {L}$
hierarchies agree on limit levels, so the distinction will not be relevant for our purposes. A key theorem he proves is that levels of the
$\mathrm {L}$
hierarchies agree on limit levels, so the distinction will not be relevant for our purposes. A key theorem he proves is that levels of the
![]() $\mathrm {J}$
hierarchy have
$\mathrm {J}$
hierarchy have
![]() $\Sigma _k$
Skolem functions for all k, uniformly so. Let us give a version of this appropriate to our context.
$\Sigma _k$
Skolem functions for all k, uniformly so. Let us give a version of this appropriate to our context.
Definition 4.2.1. Consider a model U of a strong enough fragment of
![]() $\mathsf {ZFC}$
and fix finite k. We say that U has a
$\mathsf {ZFC}$
and fix finite k. We say that U has a
![]() $\Sigma _k$
Skolem function when there is a
$\Sigma _k$
Skolem function when there is a
![]() $\Sigma _k$
definition for the function
$\Sigma _k$
definition for the function
![]() $h: \omega ^U \times U \to U$
such that, for every
$h: \omega ^U \times U \to U$
such that, for every
![]() $\Sigma _k$
formula
$\Sigma _k$
formula
![]() $\varphi $
,
$\varphi $
,
Theorem 4.2.2 (Jensen’s
 $\Sigma _\ell $
uniformization theorem)
$\Sigma _\ell $
uniformization theorem)
Fix
![]() $1 \le k \le \ell $
. There is a
$1 \le k \le \ell $
. There is a
![]() $\Sigma _k$
formula
$\Sigma _k$
formula
![]() $\psi $
such that
$\psi $
such that
![]() $\mathsf {ZFC}^-_\ell + \mathrm {V} = \mathrm {L}$
proves that
$\mathsf {ZFC}^-_\ell + \mathrm {V} = \mathrm {L}$
proves that
![]() $\psi $
defines a
$\psi $
defines a
![]() $\Sigma _k$
Skolem function. That is, if
$\Sigma _k$
Skolem function. That is, if
![]() $U \models \mathsf {ZFC}^-_\ell + \mathrm {V} = \mathrm {L}$
then the function
$U \models \mathsf {ZFC}^-_\ell + \mathrm {V} = \mathrm {L}$
then the function
![]() $h = \psi ^U$
defined by
$h = \psi ^U$
defined by
![]() $\psi $
in U is a
$\psi $
in U is a
![]() $\Sigma _k$
Skolem function for U.
$\Sigma _k$
Skolem function for U.
This is a combination of some results in [Reference Jensen22], mainly Lemmas 2.9. and 3.4(i) together with the technique of standard codes developed in Section 4. A recent version of these can be found in the recent [Reference Jensen23] where Jensen develops the fine structure theory in more detail, mentioning more precisely where and how uniformization applies absolutely. Jensen presents his work in the context of transitive models with
![]() $\mathsf {ZFC}$
as the background theory. A careful read-through of his arguments makes clear that this background theory is overkill. One does not need the Powerset axiom to carry out the inductive construction, and the amount of Collection and Separation needed does not exceed the complexity of the desired Skolem function. Rather than multiply this paper’s length by giving a reconstruction of Jensen’s arguments with a careful accounting of the axioms used, we point the reader to the above-cited works. We also point to [Reference Dodd5] for an analysis of the minimal axioms—less than even
$\mathsf {ZFC}$
as the background theory. A careful read-through of his arguments makes clear that this background theory is overkill. One does not need the Powerset axiom to carry out the inductive construction, and the amount of Collection and Separation needed does not exceed the complexity of the desired Skolem function. Rather than multiply this paper’s length by giving a reconstruction of Jensen’s arguments with a careful accounting of the axioms used, we point the reader to the above-cited works. We also point to [Reference Dodd5] for an analysis of the minimal axioms—less than even
![]() $\mathsf {KP}$
—needed to carry out the basic constructions of the rudimentary functions.
$\mathsf {KP}$
—needed to carry out the basic constructions of the rudimentary functions.
Lemma 4.2.3. Fix
![]() $k \ge 1$
. Work over
$k \ge 1$
. Work over
![]() $\mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {L}$
Consider the unrolled model
$\mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {L}$
Consider the unrolled model
![]() $U \models \mathsf {ZFC}^-_{\mathrm {I},k} + \mathrm {V} = \mathrm {L}$
, and let
$U \models \mathsf {ZFC}^-_{\mathrm {I},k} + \mathrm {V} = \mathrm {L}$
, and let
![]() $\kappa $
denote the largest cardinal in this model. Then there is a definition for a sequence
$\kappa $
denote the largest cardinal in this model. Then there is a definition for a sequence
![]() ${\left \langle \alpha _i : i \in \omega \right \rangle }$
so that
${\left \langle \alpha _i : i \in \omega \right \rangle }$
so that
![]() $\bigcup _i \mathrm {L}_{\alpha _i} \models \mathsf {ZFC}^-_{\mathrm {I},k}$
, with the same largest cardinal
$\bigcup _i \mathrm {L}_{\alpha _i} \models \mathsf {ZFC}^-_{\mathrm {I},k}$
, with the same largest cardinal
![]() $\kappa $
. Consequently the property “the sequence
$\kappa $
. Consequently the property “the sequence
![]() ${\left \langle \alpha _i \right \rangle }$
is cofinal in the ordinals” is expressible.
${\left \langle \alpha _i \right \rangle }$
is cofinal in the ordinals” is expressible.
Before the proof let’s clear up a potential misunderstanding. The union
![]() $\bigcup _i \mathrm {L}_{\alpha _i}$
refers to the direct limit of the system of models
$\bigcup _i \mathrm {L}_{\alpha _i}$
refers to the direct limit of the system of models
![]() $\mathrm {L}_{\alpha _i}$
, each equipped with the membership relation from the unrolled model. If we’re working over a transitive model then this union is itself a level of the
$\mathrm {L}_{\alpha _i}$
, each equipped with the membership relation from the unrolled model. If we’re working over a transitive model then this union is itself a level of the
![]() $\mathrm {L}$
hierarchy. But in a nonstandard model there might be a cut and the sequence
$\mathrm {L}$
hierarchy. But in a nonstandard model there might be a cut and the sequence
![]() $\alpha _i$
doesn’t have a supremum in the model. (Indeed, that is exactly what happens when the sequence is cofinal, which it will be in the models we are interested in.) After all, while the sequence is definable, its definition is too complex for the weak theory satisfied by the model to guarantee its supremum exists as an element of the model. Nonetheless, the direct system is definable and hence its direct limit is also definable.
$\alpha _i$
doesn’t have a supremum in the model. (Indeed, that is exactly what happens when the sequence is cofinal, which it will be in the models we are interested in.) After all, while the sequence is definable, its definition is too complex for the weak theory satisfied by the model to guarantee its supremum exists as an element of the model. Nonetheless, the direct system is definable and hence its direct limit is also definable.
Proof Consider a model
![]() $(M,\mathcal {M}) \models \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {L}$
and work in its unrolled model
$(M,\mathcal {M}) \models \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {L}$
and work in its unrolled model
![]() $U \models \mathsf {ZFC}^-_{\mathrm {I},k}$
. From Theorem 4.2.2, we have a
$U \models \mathsf {ZFC}^-_{\mathrm {I},k}$
. From Theorem 4.2.2, we have a
![]() $\Sigma _k$
Skolem function h for U. Define the
$\Sigma _k$
Skolem function h for U. Define the
![]() $\omega $
-sequence
$\omega $
-sequence
![]() ${\left \langle \alpha _i \right \rangle }$
as follows: Start with
${\left \langle \alpha _i \right \rangle }$
as follows: Start with
![]() $\alpha _0 = \kappa $
and at successors we will pick
$\alpha _0 = \kappa $
and at successors we will pick
![]() $\alpha _{i+1}$
to be give a level of the
$\alpha _{i+1}$
to be give a level of the
![]() $\mathrm {L}$
hierarchy which is closed under h for inputs from
$\mathrm {L}$
hierarchy which is closed under h for inputs from
![]() $\mathrm {L}_{\alpha _i}$
. To this purpose, define the class function
$\mathrm {L}_{\alpha _i}$
. To this purpose, define the class function
The function h is
![]() $\Sigma _k$
and being
$\Sigma _k$
and being
![]() $\mathrm {L}_{\alpha }$
is a
$\mathrm {L}_{\alpha }$
is a
![]() $\Sigma _1$
property of
$\Sigma _1$
property of
![]() $\alpha $
. So in all W is
$\alpha $
. So in all W is
![]() $\Sigma _k$
, and so
$\Sigma _k$
, and so
![]() $W(\alpha )$
is a set in U. Then, set
$W(\alpha )$
is a set in U. Then, set
If
![]() $\psi (y,x)$
is
$\psi (y,x)$
is
![]() $\Sigma _k$
then the property “
$\Sigma _k$
then the property “
![]() $\mathrm {L}_\xi $
contains
$\mathrm {L}_\xi $
contains
![]() $h(\ulcorner {\psi }\urcorner ,x)$
” is also
$h(\ulcorner {\psi }\urcorner ,x)$
” is also
![]() $\Sigma _k$
in parameters
$\Sigma _k$
in parameters
![]() $\xi $
and x. So this definition really does give that
$\xi $
and x. So this definition really does give that
![]() $\mathrm {L}_{\alpha _{i+1}}$
is closed under h for inputs from
$\mathrm {L}_{\alpha _{i+1}}$
is closed under h for inputs from
![]() $\mathrm {L}_{\alpha _i}$
.
$\mathrm {L}_{\alpha _i}$
.
We can always continue the construction one more step, and so the set of i for which
![]() $\alpha _i$
is defined forms an inductive subset of
$\alpha _i$
is defined forms an inductive subset of
![]() $\omega $
. So by
$\omega $
. So by
![]() $\mathsf {SOR}$
it must be all of
$\mathsf {SOR}$
it must be all of
![]() $\omega $
.
$\omega $
.
To show that
![]() $N = \bigcup _i \mathrm {L}_{\alpha _i} \models \mathsf {ZFC}^-_{\mathrm {I},k}$
we first show that any
$N = \bigcup _i \mathrm {L}_{\alpha _i} \models \mathsf {ZFC}^-_{\mathrm {I},k}$
we first show that any
![]() $\Sigma _k$
formula
$\Sigma _k$
formula
![]() $\theta (y,x)$
with a parameter x in one of the
$\theta (y,x)$
with a parameter x in one of the
![]() $\mathrm {L}_{\alpha _i}$
reflects. To this end fix such
$\mathrm {L}_{\alpha _i}$
reflects. To this end fix such
![]() $\theta (y,x)$
and
$\theta (y,x)$
and
![]() $x \in \mathrm {L}_{\alpha _i}$
. Suppose that
$x \in \mathrm {L}_{\alpha _i}$
. Suppose that
![]() $U \models \exists y\ \theta (y,x)$
. Then
$U \models \exists y\ \theta (y,x)$
. Then
![]() $U \models \theta (h(\ulcorner \theta ,x\urcorner ))$
. But
$U \models \theta (h(\ulcorner \theta ,x\urcorner ))$
. But
![]() $h(\ulcorner \theta ,x\urcorner ) \in \mathrm {L}_{\alpha _{i+1}}$
. By Tarski–Vaught we get that N is a
$h(\ulcorner \theta ,x\urcorner ) \in \mathrm {L}_{\alpha _{i+1}}$
. By Tarski–Vaught we get that N is a
![]() $\Sigma _k$
elementary submodel of U. Now by a standard argument we get that
$\Sigma _k$
elementary submodel of U. Now by a standard argument we get that
![]() $N \models \Sigma _k$
-Replacement. Namely, suppose there is
$N \models \Sigma _k$
-Replacement. Namely, suppose there is
![]() $a \in N$
so that for each
$a \in N$
so that for each
![]() $x \in a$
there’s a unique y so that
$x \in a$
there’s a unique y so that
![]() $\varphi (x,y)$
, where
$\varphi (x,y)$
, where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Sigma _k$
formula, possibly with parameters. Then there’s i so that a and all parameters are in
$\Sigma _k$
formula, possibly with parameters. Then there’s i so that a and all parameters are in
![]() $\mathrm {L}_{\alpha _i}$
. Using that N is
$\mathrm {L}_{\alpha _i}$
. Using that N is
![]() $\Sigma _k$
-elementary in U, we get that the witnesses y must all be in
$\Sigma _k$
-elementary in U, we get that the witnesses y must all be in
![]() $\mathrm {L}_{\alpha _{i+1}}$
, witnessing that instance of Replacement. This immediately implies that
$\mathrm {L}_{\alpha _{i+1}}$
, witnessing that instance of Replacement. This immediately implies that
![]() $N \models \Sigma _k$
-Separation and Collection, where for the second fact we use that N has a definable global well-order. That
$N \models \Sigma _k$
-Separation and Collection, where for the second fact we use that N has a definable global well-order. That
![]() $N \models \mathrm {V} = \mathrm {L}$
is immediate. And N has the same
$N \models \mathrm {V} = \mathrm {L}$
is immediate. And N has the same
![]() $\kappa $
as its largest cardinal by an inductive argument. Trivially
$\kappa $
as its largest cardinal by an inductive argument. Trivially
![]() $\mathrm {L}_{\alpha _0} = \mathrm {L}_\kappa $
has cardinality
$\mathrm {L}_{\alpha _0} = \mathrm {L}_\kappa $
has cardinality
![]() $\kappa $
. And then inductively
$\kappa $
. And then inductively
![]() $\mathrm {L}_{\alpha _{i+1}}$
is a union of
$\mathrm {L}_{\alpha _{i+1}}$
is a union of
![]() $\kappa $
many sets of size
$\kappa $
many sets of size
![]() $\kappa $
whence it’s also of cardinality
$\kappa $
whence it’s also of cardinality
![]() $\kappa $
.
$\kappa $
.
This theorem allows us a characterization of models of class theory which think they are the minimum model of
![]() $\mathsf {KMCC}_k$
. Namely, let
$\mathsf {KMCC}_k$
. Namely, let
![]() $\mathrm {Class} = \mathrm {MinMod}_k$
be the conjunction of
$\mathrm {Class} = \mathrm {MinMod}_k$
be the conjunction of
![]() $\mathrm {Class} = \mathrm {L}$
and “in the unrolling the sequence
$\mathrm {Class} = \mathrm {L}$
and “in the unrolling the sequence
![]() ${\left \langle \alpha _i \right \rangle }$
is cofinal in the ordinals”. Moreover, we can express whether a model is a width-extension of a model of
${\left \langle \alpha _i \right \rangle }$
is cofinal in the ordinals”. Moreover, we can express whether a model is a width-extension of a model of
![]() $\mathrm {Class} = \mathrm {MinMod}_k$
, by expressing that the second-order constructible classes of that model satisfy
$\mathrm {Class} = \mathrm {MinMod}_k$
, by expressing that the second-order constructible classes of that model satisfy
![]() $\mathrm {Class} = \mathrm {MinMod}_k$
.
$\mathrm {Class} = \mathrm {MinMod}_k$
.
As in the transitive case, having a definable cofinal sequence in the ordinals of the unrolled model allows us to define a code for the hyperclass of all classes.
Lemma 4.2.4. Fix
![]() $k \ge 1$
. Let
$k \ge 1$
. Let
![]() $(M,\mathcal {M}) \models \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {MinMod}_k$
. Then over
$(M,\mathcal {M}) \models \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {MinMod}_k$
. Then over
![]() $(M,\mathcal {M})$
there is a definition for a code
$(M,\mathcal {M})$
there is a definition for a code
![]() $\mathrm {T}_{\mathcal {M}}$
for
$\mathrm {T}_{\mathcal {M}}$
for
![]() $\mathcal {M}$
. Moreover, this definition can be chosen to be absolute across all width-extensions of
$\mathcal {M}$
. Moreover, this definition can be chosen to be absolute across all width-extensions of
![]() $(M,\mathcal {M})$
.
$(M,\mathcal {M})$
.
Proof Sketch
As in Corollary 3.2.4, but since our cofinal sequence has length
![]() $\omega $
we define the code to consist of triples
$\omega $
we define the code to consist of triples
![]() $(i,j,x)$
where
$(i,j,x)$
where
![]() $i \in \omega $
,
$i \in \omega $
,
![]() $j \in \mathrm {Ord}$
, and x is a set. To make the definition absolute across width-extensions, relativize it to second-order
$j \in \mathrm {Ord}$
, and x is a set. To make the definition absolute across width-extensions, relativize it to second-order
![]() $\mathrm {L}$
.
$\mathrm {L}$
.
We can also do this for Cohen generics over a model of
![]() $\mathrm {MinMod}_k$
, as in Lemma 3.2.5.
$\mathrm {MinMod}_k$
, as in Lemma 3.2.5.
Lemma 4.2.5. Fix
![]() $k \ge 1$
. Let
$k \ge 1$
. Let
![]() $(M,\mathcal {M}) \models \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {MinMod}_k$
and suppose
$(M,\mathcal {M}) \models \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {MinMod}_k$
and suppose
![]() $\mathrm {C} \subseteq M$
is a generic over
$\mathrm {C} \subseteq M$
is a generic over
![]() $(M,\mathcal {M})$
for
$(M,\mathcal {M})$
for
![]() $\mathrm {Add}(\mathrm {Ord},1)$
which is second-order definable over
$\mathrm {Add}(\mathrm {Ord},1)$
which is second-order definable over
![]() $(M,\mathcal {M})$
. Then there is a definition for a code
$(M,\mathcal {M})$
. Then there is a definition for a code
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
which is absolute across all width-extensions of
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
which is absolute across all width-extensions of
![]() $(M,\mathcal {M})$
.
$(M,\mathcal {M})$
.
The extension by
![]() $\mathrm {C}$
is a width-extension, so it is among those extensions for which the definition of
$\mathrm {C}$
is a width-extension, so it is among those extensions for which the definition of
![]() $\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
is absolute.
$\mathrm {T}_{\mathcal {M}}(\mathrm {C})$
is absolute.
Finally, we must say how to define
![]() $\mathrm {C}$
. But there is no new content here. Work in a model of
$\mathrm {C}$
. But there is no new content here. Work in a model of
![]() $\mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {MinMod}_k$
. Using the code
$\mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {MinMod}_k$
. Using the code
![]() $\mathrm {T}_{\mathcal {M}}$
we extract a canonical
$\mathrm {T}_{\mathcal {M}}$
we extract a canonical
![]() $\mathrm {Ord}$
-sequence of the dense subclasses of
$\mathrm {Ord}$
-sequence of the dense subclasses of
![]() $\mathrm {Add}(\mathrm {Ord},1)$
in the model. We extend to meet these subclasses one at a time, always using the
$\mathrm {Add}(\mathrm {Ord},1)$
in the model. We extend to meet these subclasses one at a time, always using the
![]() $\mathrm {L}$
-order to make choices of how to extend. Here
$\mathrm {L}$
-order to make choices of how to extend. Here
![]() $\mathsf {SOR}$
comes into play to ensure this construction never takes us outside the model. So in
$\mathsf {SOR}$
comes into play to ensure this construction never takes us outside the model. So in
![]() $\mathrm {Ord}$
many steps we produce
$\mathrm {Ord}$
many steps we produce
![]() $\mathrm {C}$
. And any extension which defines
$\mathrm {C}$
. And any extension which defines
![]() $\mathrm {T}_{\mathcal {M}}$
the same will define
$\mathrm {T}_{\mathcal {M}}$
the same will define
![]() $\mathrm {C}$
the same.
$\mathrm {C}$
the same.
Let
![]() $\mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
be the second-order formula which expresses that the classes are precisely those which appear in the code
$\mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
be the second-order formula which expresses that the classes are precisely those which appear in the code
![]() $\mathrm {T}_{\mathcal {M}}[\mathrm {C}]$
. Intuitive, this formula expresses that the model is the forcing extension of the minimum model of
$\mathrm {T}_{\mathcal {M}}[\mathrm {C}]$
. Intuitive, this formula expresses that the model is the forcing extension of the minimum model of
![]() $\mathsf {KMCC}_k$
by the canonical choice of a Cohen generic.
$\mathsf {KMCC}_k$
by the canonical choice of a Cohen generic.
Following the same interpretation strategy as before, we get that any model of
![]() $\mathrm {Class} = \mathrm {MinMod}_k$
is bi-interpretable with its extension by
$\mathrm {Class} = \mathrm {MinMod}_k$
is bi-interpretable with its extension by
![]() $\mathrm {C}$
.
$\mathrm {C}$
.
Theorem 4.2.6. Fix
![]() $k \ge 1$
. The following two theories are bi-interpretable.
$k \ge 1$
. The following two theories are bi-interpretable.
-
(1)
 $D_k = \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {MinMod}_k$
.
$D_k = \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {MinMod}_k$
. -
(2)
 $U_k = \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
.
$U_k = \mathsf {KMCC}_k + \mathsf {SOR} + \mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
.
Corollary 4.2.7. Fix
![]() $k \ge 1$
. The theories
$k \ge 1$
. The theories
![]() $\mathsf {KMCC}_k$
and
$\mathsf {KMCC}_k$
and
![]() $\mathsf {KMCC}_k + \mathsf {SOR}$
are not tight.
$\mathsf {KMCC}_k + \mathsf {SOR}$
are not tight.
5 Non-tightness in second-order arithmetic
The constructions used in the previous section also work in the context of second-order arithmetic. However, there are enough subtleties and notational differences in arithmetic context that for ease of exposition we discuss it separately in this section. Most proofs carry over mutatis mutandis from the class theory context, and we leave it to the interested reader to rewrite the proofs with the changed details. We state some facts about models of second-order arithmetic without proof, and we point the reader to Simpson’s book on the subject [Reference Simpson33], especially Chapter VII, for proofs and detailed references.
In the class theory context, to get the failure of tightness we added the full second-order Replacement schema to our theories. In the arithmetic context, the analogue is the full Induction schema, i.e., the instances of Induction for every second-order formula, and we will include it in our theories to ensure constructions go through the model’s full
![]() $\omega $
.
$\omega $
.
The strategy is the same as in class theory. For fragments of second-order arithmetic we can write down a theory which characterizes a minimum model. We can define a canonical code for this minimum model, and thereby define a canonical Cohen extension of the minimum model. These two models are bi-interpretable. Of course, with the nonstandardness phenomenon there is no hope for a notion of minimum absolute between all models of the theory. But we can get a sufficiently absolute notion to enable the bi-interpretation, so we get the fragment of
![]() $\mathsf {Z}_2$
cannot be tight.
$\mathsf {Z}_2$
cannot be tight.
First we discuss the analogue of
![]() $\mathsf {GB}$
. The theory
$\mathsf {GB}$
. The theory
![]() $\mathsf {ACA}_0$
has as its principle axioms Induction and Comprehension for arithmetical formulae. If you strengthen Induction to the full schema, over all second-order formulae, you get the theory
$\mathsf {ACA}_0$
has as its principle axioms Induction and Comprehension for arithmetical formulae. If you strengthen Induction to the full schema, over all second-order formulae, you get the theory
![]() $\mathsf {ACA}$
. Every
$\mathsf {ACA}$
. Every
![]() $\omega $
-model of
$\omega $
-model of
![]() $\mathsf {ACA}_0$
—viz. a model whose numbers are isomorphic to
$\mathsf {ACA}_0$
—viz. a model whose numbers are isomorphic to
![]() $\omega $
—automatically satisfies full
$\omega $
—automatically satisfies full
![]() $\mathsf {ACA}$
. But for nonstandard models the theories diverge. For instance, analogous to the situation with
$\mathsf {ACA}$
. But for nonstandard models the theories diverge. For instance, analogous to the situation with
![]() $\mathsf {GB}$
and
$\mathsf {GB}$
and
![]() $\mathsf {SOR}$
, over
$\mathsf {SOR}$
, over
![]() $\mathsf {ACA}$
you can prove that the
$\mathsf {ACA}$
you can prove that the
![]() $\Sigma _k$
-satisfaction class exists for all k, even nonstandard. Whereas with just
$\Sigma _k$
-satisfaction class exists for all k, even nonstandard. Whereas with just
![]() $\mathsf {ACA}_0$
you are only guaranteed to have such for standard k. The reason, of course, is that
$\mathsf {ACA}_0$
you are only guaranteed to have such for standard k. The reason, of course, is that
![]() $(M,\operatorname {Def}(M))$
is always a model of
$(M,\operatorname {Def}(M))$
is always a model of
![]() $\mathsf {ACA}_0$
for any
$\mathsf {ACA}_0$
for any
![]() $M \models \mathsf {PA}$
, and no nonstandard
$M \models \mathsf {PA}$
, and no nonstandard
![]() $\Sigma _k$
-satisfaction class can be definable.
$\Sigma _k$
-satisfaction class can be definable.
Following the
![]() $\mathsf {GB}$
context, we can write down a theory which identifies the minimum
$\mathsf {GB}$
context, we can write down a theory which identifies the minimum
![]() $\omega $
-model, namely the arithmetical reals, among all
$\omega $
-model, namely the arithmetical reals, among all
![]() $\omega $
-models. Using full Induction, this will allow a definition sufficiently absolute among nonstandard models to enable two distinct but bi-interpretable extensions of
$\omega $
-models. Using full Induction, this will allow a definition sufficiently absolute among nonstandard models to enable two distinct but bi-interpretable extensions of
![]() $\mathsf {ACA}$
.
$\mathsf {ACA}$
.
There is a second-order definition for the (first-order) satisfaction predicate, call it
![]() $\mathrm {T}$
. Indeed, the same definition as before—viz. the union of the
$\mathrm {T}$
. Indeed, the same definition as before—viz. the union of the
![]() $\Sigma _k$
-satisfaction classes—will do, modulo the details of Gödel coding. Note that full Induction is used to ensure there is a
$\Sigma _k$
-satisfaction classes—will do, modulo the details of Gödel coding. Note that full Induction is used to ensure there is a
![]() $\Sigma _k$
-satisfaction predicate for every k in the model. This makes possible a theory D expressing
$\Sigma _k$
-satisfaction predicate for every k in the model. This makes possible a theory D expressing
![]() $\mathsf {ACA}\ +$
“every set is arithmetical” and a theory U expressing
$\mathsf {ACA}\ +$
“every set is arithmetical” and a theory U expressing
![]() $\mathsf {ACA}\ +$
“there is a canonical Cohen-generic
$\mathsf {ACA}\ +$
“there is a canonical Cohen-generic
![]() $\mathrm {C}$
over the arithmetical sets and every set is arithmetical in
$\mathrm {C}$
over the arithmetical sets and every set is arithmetical in
![]() $\mathrm {C}$
.” These two theories are then bi-interpretable, with two key points—proved much the same as the class theoretic case—being that forcing preserves full and induction and the definition of
$\mathrm {C}$
.” These two theories are then bi-interpretable, with two key points—proved much the same as the class theoretic case—being that forcing preserves full and induction and the definition of
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
All in all, we get the following result.
Theorem 5.0.1. The theory
![]() $\mathsf {ACA}$
is not tight. Consequently, any weakening of
$\mathsf {ACA}$
is not tight. Consequently, any weakening of
![]() $\mathsf {ACA}$
in the language of second-order arithmetic, such as
$\mathsf {ACA}$
in the language of second-order arithmetic, such as
![]() $\mathsf {ACA}_0$
, is also not tight.
$\mathsf {ACA}_0$
, is also not tight.
For stronger fragments of
![]() $\mathsf {Z}_2$
the same basic strategy works, but producing the code for the minimum model is more difficult than defining a satisfaction predicate. We start by recalling some definitions and facts.
$\mathsf {Z}_2$
the same basic strategy works, but producing the code for the minimum model is more difficult than defining a satisfaction predicate. We start by recalling some definitions and facts.
Definition 5.0.2. Fix
![]() $k \ge 1$
.
$k \ge 1$
.
-
• The theory
 $\Pi _{k}^1\text {-}\mathsf {CA}_0$
is obtained from
$\Pi _{k}^1\text {-}\mathsf {CA}_0$
is obtained from
 $\mathsf {ACA}_0$
by adding Comprehension for
$\mathsf {ACA}_0$
by adding Comprehension for
 $\Pi ^1_k$
formulae.
$\Pi ^1_k$
formulae. -
• The theory
 $\Pi _{k}^1\text {-}\mathsf {CA}$
is obtained from
$\Pi _{k}^1\text {-}\mathsf {CA}$
is obtained from
 $\Pi _{k}^1\text {-}\mathsf {CA}_0$
by adding full Induction.
$\Pi _{k}^1\text {-}\mathsf {CA}_0$
by adding full Induction. -
• The theory
 $\Sigma _{k}^1\text {-}\mathsf {AC}_0$
is obtained from
$\Sigma _{k}^1\text {-}\mathsf {AC}_0$
is obtained from
 $\Pi _{k}^1\text {-}\mathsf {CA}$
by adding the
$\Pi _{k}^1\text {-}\mathsf {CA}$
by adding the
 $\Sigma ^1_k$
-Choice schema. This schema is the arithmetic counterpart to the
$\Sigma ^1_k$
-Choice schema. This schema is the arithmetic counterpart to the
 $\Sigma ^1_k$
-Class Collection schema (cf. Definition 2.0.3).
$\Sigma ^1_k$
-Class Collection schema (cf. Definition 2.0.3). -
• The theory
 $\Sigma _{k}^1\text {-}\mathsf {AC}$
is obtained from
$\Sigma _{k}^1\text {-}\mathsf {AC}$
is obtained from
 $\Sigma _{k}^1\text {-}\mathsf {AC}_0$
by adding full Induction.
$\Sigma _{k}^1\text {-}\mathsf {AC}_0$
by adding full Induction.
The theory
![]() $\mathsf {ATR}_0$
, a strict subtheory of
$\mathsf {ATR}_0$
, a strict subtheory of
![]() $\Pi _1^1\text {-}\mathsf {CA}_0$
, is strong enough to carry out the unrolling construction. As such, theories of arithmetic which extend
$\Pi _1^1\text {-}\mathsf {CA}_0$
, is strong enough to carry out the unrolling construction. As such, theories of arithmetic which extend
![]() $\mathsf {ATR}_0$
are bi-interpretable with certain set theories. These theories are strong enough to carry out the construction of
$\mathsf {ATR}_0$
are bi-interpretable with certain set theories. These theories are strong enough to carry out the construction of
![]() $\mathrm {L}$
. Restricting to the constructible sets gives fragments of the AC schema, so
$\mathrm {L}$
. Restricting to the constructible sets gives fragments of the AC schema, so
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
does not exceed
$\Sigma _{k}^1\text {-}\mathsf {AC}$
does not exceed
![]() $\Pi _{k}^1\text {-}\mathsf {CA}$
in consistency strength. Unlike in class theory, however, weak enough fragments of the
$\Pi _{k}^1\text {-}\mathsf {CA}$
in consistency strength. Unlike in class theory, however, weak enough fragments of the
![]() $\mathsf {AC}$
schema are outright provable, without any assumption of every set being constructible.
$\mathsf {AC}$
schema are outright provable, without any assumption of every set being constructible.
Theorem 5.0.3. The
![]() $\Sigma ^1_1$
-Choice schema is a consequence of
$\Sigma ^1_1$
-Choice schema is a consequence of
![]() $\mathsf {ATR}_0$
, and over
$\mathsf {ATR}_0$
, and over
![]() $\mathsf {ATR}_0$
the
$\mathsf {ATR}_0$
the
![]() $\Sigma ^1_2$
-Choice schema is equivalent to
$\Sigma ^1_2$
-Choice schema is equivalent to
![]() $\Delta ^1_2$
-Comprehension. For
$\Delta ^1_2$
-Comprehension. For
![]() $k> 2$
, the
$k> 2$
, the
![]() $\Sigma ^1_k$
-Choice schema is a consequence of
$\Sigma ^1_k$
-Choice schema is a consequence of
![]() $\Pi _{k}^1\text {-}\mathsf {CA}_0\ +$
“there is a real from which every real is constructible.”
$\Pi _{k}^1\text {-}\mathsf {CA}_0\ +$
“there is a real from which every real is constructible.”
For our purposes we are looking at models which satisfy that every real is constructible, or Cohen-extensions thereof. So we will only be looking at models of
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
. (This will include
$\Sigma _{k}^1\text {-}\mathsf {AC}$
. (This will include
![]() $\Sigma _{1}^1\text {-}\mathsf {AC} = \Pi _1^1\text {-}\mathsf {CA}$
and
$\Sigma _{1}^1\text {-}\mathsf {AC} = \Pi _1^1\text {-}\mathsf {CA}$
and
![]() $\Sigma _{2}^1\text {-}\mathsf {AC} = \Pi _{2}^1\text {-}\mathsf {CA}$
, but for the sake of uniform notation we will use the former names.) Here are bi-interpretation results for these theories.
$\Sigma _{2}^1\text {-}\mathsf {AC} = \Pi _{2}^1\text {-}\mathsf {CA}$
, but for the sake of uniform notation we will use the former names.) Here are bi-interpretation results for these theories.
Theorem 5.0.4. The following pairs of theories are bi-interpretable.
-
•
 $\mathsf {Z}_2 + \Sigma ^1_\infty $
-
$\mathsf {Z}_2 + \Sigma ^1_\infty $
-
 $\mathsf {CA}$
and
$\mathsf {CA}$
and
 $\mathsf {ZFC}^-$
plus “every set is countable.”
$\mathsf {ZFC}^-$
plus “every set is countable.” -
• For
 $k \ge 1$
,
$k \ge 1$
,
 $\Pi _{k+1}^1\text {-}\mathsf {CA}_0$
and
$\Pi _{k+1}^1\text {-}\mathsf {CA}_0$
and
 $\mathsf {ZFC}^-_{k}$
plus “every set is countable.”
$\mathsf {ZFC}^-_{k}$
plus “every set is countable.”
In the class theoretic case, the indexing was the same. Here they are off by one. The culprit is well-foundedness. In class theory this is a first-order property, whereas in arithmetic it is
![]() $\Pi ^1_1$
-universal. Because of this misaligned indexing, the situation with
$\Pi ^1_1$
-universal. Because of this misaligned indexing, the situation with
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
is different from the stronger theories. We discuss it first.
$\Sigma _{1}^1\text {-}\mathsf {AC}$
is different from the stronger theories. We discuss it first.
Theorem 5.0.5. The minimum
![]() $\beta $
-model of
$\beta $
-model of
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
consists of the reals in
$\Sigma _{1}^1\text {-}\mathsf {AC}$
consists of the reals in
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
, where
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
, where
![]() $\omega _\omega ^{\mathrm {CK}}$
is the supremum of the first
$\omega _\omega ^{\mathrm {CK}}$
is the supremum of the first
![]() $\omega $
many admissible ordinals.
$\omega $
many admissible ordinals.
Note that the inclusion of full Induction means that any model of
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
thinks the n-th admissible ordinal
$\Sigma _{1}^1\text {-}\mathsf {AC}$
thinks the n-th admissible ordinal
![]() $\omega _n^{\mathrm {CK}}$
exists even for nonstandard n. This is because
$\omega _n^{\mathrm {CK}}$
exists even for nonstandard n. This is because
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}_0$
is strong enough to prove that the admissible ordinals are unbounded and so the set of such n is inductive. And over
$\Sigma _{1}^1\text {-}\mathsf {AC}_0$
is strong enough to prove that the admissible ordinals are unbounded and so the set of such n is inductive. And over
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
we can define the sequence of the
$\Sigma _{1}^1\text {-}\mathsf {AC}$
we can define the sequence of the
![]() $\omega _n^{\mathrm {CK}}$
. From this sequence we can extract a canonical code of all the reals in
$\omega _n^{\mathrm {CK}}$
. From this sequence we can extract a canonical code of all the reals in
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
, as in the similar argument for strong fragments of
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
, as in the similar argument for strong fragments of
![]() $\mathsf {KM}$
. From this code we can define, via a second-order formula, a canonical choice for a Cohen real
$\mathsf {KM}$
. From this code we can define, via a second-order formula, a canonical choice for a Cohen real
![]() $\mathrm {C}$
which is generic over
$\mathrm {C}$
which is generic over
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
.
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
.
It is straightforward to formulate an axiom asserting over
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
that every set is in
$\Sigma _{1}^1\text {-}\mathsf {AC}$
that every set is in
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
. Namely, this axiom asserts that for every set X there is an integer n so that there is a length n sequence of well-orders
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
. Namely, this axiom asserts that for every set X there is an integer n so that there is a length n sequence of well-orders
![]() $\gamma _i$
so that each
$\gamma _i$
so that each
![]() $\gamma _i$
is admissible,
$\gamma _i$
is admissible,
![]() $\gamma _0 = \omega $
, there are no admissibles between
$\gamma _0 = \omega $
, there are no admissibles between
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\gamma _{i+1}$
, and X is in
$\gamma _{i+1}$
, and X is in
![]() $\mathrm {L}_{\gamma _n}$
. Call this axiom
$\mathrm {L}_{\gamma _n}$
. Call this axiom
![]() $\mathrm {Class} = \mathrm {Adm}_\omega $
. Similarly, we can formulate an axiom
$\mathrm {Class} = \mathrm {Adm}_\omega $
. Similarly, we can formulate an axiom
![]() $\mathrm {Class} = \mathrm {Adm}_\omega [\mathrm {C}]$
which asserts that
$\mathrm {Class} = \mathrm {Adm}_\omega [\mathrm {C}]$
which asserts that
![]() $\mathrm {C}$
exists and every set is in
$\mathrm {C}$
exists and every set is in
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}[\mathrm {C}]$
, where
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}[\mathrm {C}]$
, where
![]() $\mathrm {C}$
is definable Cohen generic over the reals in
$\mathrm {C}$
is definable Cohen generic over the reals in
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
. We follow the same strategy as before to define
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
. We follow the same strategy as before to define
![]() $\mathrm {C}$
, using the canonical code of
$\mathrm {C}$
, using the canonical code of
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
.
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
.
Putting this all together, we get that the theories
![]() $\Sigma _{1}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {Adm}_\omega $
and
$\Sigma _{1}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {Adm}_\omega $
and
![]() $\Sigma _{1}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {Adm}_\omega [\mathrm {C}]$
are bi-interpretable. A key point is, a model of
$\Sigma _{1}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {Adm}_\omega [\mathrm {C}]$
are bi-interpretable. A key point is, a model of
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
and any Cohen-extension thereof will have the same well-orders and agree on which well-orders give admissible ordinals. So they will define the canonical code for the reals in
$\Sigma _{1}^1\text {-}\mathsf {AC}$
and any Cohen-extension thereof will have the same well-orders and agree on which well-orders give admissible ordinals. So they will define the canonical code for the reals in
![]() $\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
the same, and thereby define
$\mathrm {L}_{\omega _\omega ^{\mathrm {CK}}}$
the same, and thereby define
![]() $\mathrm {C}$
the same.
$\mathrm {C}$
the same.
Theorem 5.0.6. The theory
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}(= \Pi _1^1\text {-}\mathsf {CA})$
is not tight. Consequently, any weakening of
$\Sigma _{1}^1\text {-}\mathsf {AC}(= \Pi _1^1\text {-}\mathsf {CA})$
is not tight. Consequently, any weakening of
![]() $\Sigma _{1}^1\text {-}\mathsf {AC}$
in the language of second-order arithmetic, such as
$\Sigma _{1}^1\text {-}\mathsf {AC}$
in the language of second-order arithmetic, such as
![]() $\Pi _1^1\text {-}\mathsf {CA}_0$
, is also not tight.
$\Pi _1^1\text {-}\mathsf {CA}_0$
, is also not tight.
We turn at last to
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
for
$\Sigma _{k}^1\text {-}\mathsf {AC}$
for
![]() $k \ge 2$
. For these the characterization of the least
$k \ge 2$
. For these the characterization of the least
![]() $\beta $
-model is more complex.
$\beta $
-model is more complex.
Theorem 5.0.7. For
![]() $k> 1$
, the minimum
$k> 1$
, the minimum
![]() $\beta $
-model of
$\beta $
-model of
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
consists of the reals in
$\Sigma _{k}^1\text {-}\mathsf {AC}$
consists of the reals in
![]() $\mathrm {L}_\alpha $
where
$\mathrm {L}_\alpha $
where
![]() $\alpha $
is the least ordinal so that
$\alpha $
is the least ordinal so that
![]() $\mathrm {L}_\alpha $
satisfies
$\mathrm {L}_\alpha $
satisfies
![]() $\Pi _{k-1}$
-Separation. Equivalently,
$\Pi _{k-1}$
-Separation. Equivalently,
![]() $\alpha $
is the least ordinal so that
$\alpha $
is the least ordinal so that
![]() $\mathrm {L}_\alpha $
satisfies
$\mathrm {L}_\alpha $
satisfies
![]() $\Sigma _{k-1}$
-Replacement. Equivalently,
$\Sigma _{k-1}$
-Replacement. Equivalently,
![]() $\alpha $
is the least ordinal whose k-th projectum
$\alpha $
is the least ordinal whose k-th projectum
![]() $\rho ^\alpha _k$
is itself.
$\rho ^\alpha _k$
is itself.
Yet again, the sticking point is defining a cofinal
![]() $\omega $
-sequence in
$\omega $
-sequence in
![]() $\alpha $
. Here we can use the same fine structural facts as in Section 4.2. If
$\alpha $
. Here we can use the same fine structural facts as in Section 4.2. If
![]() $(M,\mathcal {X}) \models \Sigma _{k}^1\text {-}\mathsf {AC} +$
“every set is constructible” then it is bi-interpretable with its unrolling
$(M,\mathcal {X}) \models \Sigma _{k}^1\text {-}\mathsf {AC} +$
“every set is constructible” then it is bi-interpretable with its unrolling
![]() $U \models \mathsf {ZFC}^-_{k-1} + \mathrm {V} = \mathrm {L}$
. By Theorem 4.2.2 U has a
$U \models \mathsf {ZFC}^-_{k-1} + \mathrm {V} = \mathrm {L}$
. By Theorem 4.2.2 U has a
![]() $\Sigma _n$
Skolem function. Using this Skolem function and full Induction we can define an
$\Sigma _n$
Skolem function. Using this Skolem function and full Induction we can define an
![]() $\omega $
-sequence of ordinals
$\omega $
-sequence of ordinals
![]() $\alpha _n$
which are cofinal in what U thinks is the minimum model of
$\alpha _n$
which are cofinal in what U thinks is the minimum model of
![]() $\mathsf {ZFC}^-_{k-1}$
, as in the proof of Lemma 4.2.3. We can thus formulate an axiom expressing that U is itself this minimum model, namely by asserting that every set is in
$\mathsf {ZFC}^-_{k-1}$
, as in the proof of Lemma 4.2.3. We can thus formulate an axiom expressing that U is itself this minimum model, namely by asserting that every set is in
![]() $\mathrm {L}_{\alpha _n}$
for some n.
$\mathrm {L}_{\alpha _n}$
for some n.
All this can be translated over to the model
![]() $(M,\mathcal {X})$
of second-order arithmetic. Let
$(M,\mathcal {X})$
of second-order arithmetic. Let
![]() $\mathrm {Class} = \mathrm {MinMod}_k$
denote the formula in the language of second-order arithmetic asserting that every set is in this minimum model. Then any model of
$\mathrm {Class} = \mathrm {MinMod}_k$
denote the formula in the language of second-order arithmetic asserting that every set is in this minimum model. Then any model of
![]() $\Sigma _{k}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {MinMod}_k$
can define a canonical code for itself, using the definable
$\Sigma _{k}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {MinMod}_k$
can define a canonical code for itself, using the definable
![]() $\omega $
-sequence
$\omega $
-sequence
![]() ${\left \langle \alpha _n \right \rangle }$
of ordinals cofinal in the height of its unrolling. This code will be absolute between this model and its Cohen-extensions, because they will have the same well-orders and hence the same
${\left \langle \alpha _n \right \rangle }$
of ordinals cofinal in the height of its unrolling. This code will be absolute between this model and its Cohen-extensions, because they will have the same well-orders and hence the same
![]() $\mathrm {L}$
. From this code we can define a canonical choice for a Cohen real
$\mathrm {L}$
. From this code we can define a canonical choice for a Cohen real
![]() $\mathrm {C}$
which is generic over the minimum model. And so we can formulate an axiom
$\mathrm {C}$
which is generic over the minimum model. And so we can formulate an axiom
![]() $\mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
which asserts over
$\mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
which asserts over
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
that
$\Sigma _{k}^1\text {-}\mathsf {AC}$
that
![]() $\mathrm {C}$
exists and every real is in the extension of the minimum model by
$\mathrm {C}$
exists and every real is in the extension of the minimum model by
![]() $\mathrm {C}$
.
$\mathrm {C}$
.
Following the same interpretations as used in the previous theorems, we then conclude that
![]() $\Sigma _{k}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {MinMod}_k$
and
$\Sigma _{k}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {MinMod}_k$
and
![]() $\Sigma _{k}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
are bi-interpretable.
$\Sigma _{k}^1\text {-}\mathsf {AC} + \mathrm {Class} = \mathrm {MinMod}_k[\mathrm {C}]$
are bi-interpretable.
Theorem 5.0.8. Fix
![]() $k \ge 2$
. Then,
$k \ge 2$
. Then,
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
is not tight. Consequently, any theory weaker than
$\Sigma _{k}^1\text {-}\mathsf {AC}$
is not tight. Consequently, any theory weaker than
![]() $\Sigma _{k}^1\text {-}\mathsf {AC}$
in the language of arithmetic, such as
$\Sigma _{k}^1\text {-}\mathsf {AC}$
in the language of arithmetic, such as
![]() $\Pi _{k}^1\text {-}\mathsf {CA}$
and
$\Pi _{k}^1\text {-}\mathsf {CA}$
and
![]() $\Pi _{k}^1\text {-}\mathsf {CA}_0$
, is also not tight.
$\Pi _{k}^1\text {-}\mathsf {CA}_0$
, is also not tight.
6 Final remarks
The reader who thoroughly read the previous sections will have noticed that this article is about essentially one construction done over and over in different settings. We remark that it may be carried out in yet more settings. For example, [Reference Williams41] proves that there is a minimum
![]() $\beta $
-model of
$\beta $
-model of
![]() $\mathsf {ETR}$
, where Elementary Transfinite Recursion
$\mathsf {ETR}$
, where Elementary Transfinite Recursion
![]() $\mathsf {ETR}$
is the class theoretic analogue of
$\mathsf {ETR}$
is the class theoretic analogue of
![]() $\mathsf {ATR}_0$
. One can take their construction of the minimum
$\mathsf {ATR}_0$
. One can take their construction of the minimum
![]() $\beta $
-model of
$\beta $
-model of
![]() $\mathsf {ETR}$
and put the construction of this article in that setting, thereby showing that the minimum
$\mathsf {ETR}$
and put the construction of this article in that setting, thereby showing that the minimum
![]() $\beta $
-model of
$\beta $
-model of
![]() $\mathsf {ETR}$
is bi-interpretable with its extension by a canonical choice of Cohen generic.
$\mathsf {ETR}$
is bi-interpretable with its extension by a canonical choice of Cohen generic.
In [Reference Enayat, Eijck, Iemhoff and Joosten6], Enayat conjectures that no (proper) subsystem of the tight theories
![]() $\mathsf {PA}$
,
$\mathsf {PA}$
,
![]() $\mathsf {Z}_2$
,
$\mathsf {Z}_2$
,
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\mathsf {KM}$
can be tight. In this article, we demonstrated the non-tightness of
$\mathsf {KM}$
can be tight. In this article, we demonstrated the non-tightness of
![]() $\mathsf {KM}_k + \mathsf {SOR}$
for all natural numbers k. These results yield a natural and comprehensive collection of non-tight subtheories approximating
$\mathsf {KM}_k + \mathsf {SOR}$
for all natural numbers k. These results yield a natural and comprehensive collection of non-tight subtheories approximating
![]() $\mathsf {KM}$
. Indeed, it shows that full comprehension is the minimal level of comprehension that produces a tight theory from
$\mathsf {KM}$
. Indeed, it shows that full comprehension is the minimal level of comprehension that produces a tight theory from
![]() $\mathsf {GB}$
.
$\mathsf {GB}$
.
As we were writing this article, we learned from Ali Enayat that in forthcoming work [Reference Enayat7] he had independently proved that all finitely axiomatizable fragments of
![]() $\mathsf {PA}$
,
$\mathsf {PA}$
,
![]() $\mathsf {Z}_2$
,
$\mathsf {Z}_2$
,
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\mathsf {KM}$
are not tight. His proof provides an alternate proof of the nontightness of
$\mathsf {KM}$
are not tight. His proof provides an alternate proof of the nontightness of
![]() $\mathsf {GB}$
and
$\mathsf {GB}$
and
![]() $\mathsf {KM}_k$
, along with their arithmetical counterparts. But his argument does not apply to
$\mathsf {KM}_k$
, along with their arithmetical counterparts. But his argument does not apply to
![]() $\mathsf {GB} + \mathsf {SOR}$
,
$\mathsf {GB} + \mathsf {SOR}$
,
![]() $\mathsf {KM}_k + \mathsf {SOR}$
and their arithmetical counterparts, as the second-order Replacement schema (respectively, the second-order Induction schema) is not finitely axiomatizable. Thus, putting together Enayat’s results, our results in this article, and those of Freire and Hamkins [Reference Freire and Hamkins13], we have a substantial basis for Enayat’s conjecture. And while there still are other theories to consider in order to assert that all subtheories of KM are not tight, these would be quite unnatural subtheories.
$\mathsf {KM}_k + \mathsf {SOR}$
and their arithmetical counterparts, as the second-order Replacement schema (respectively, the second-order Induction schema) is not finitely axiomatizable. Thus, putting together Enayat’s results, our results in this article, and those of Freire and Hamkins [Reference Freire and Hamkins13], we have a substantial basis for Enayat’s conjecture. And while there still are other theories to consider in order to assert that all subtheories of KM are not tight, these would be quite unnatural subtheories.
What is missing to get the full result? With respect to class theories, we should consider proper subtheories of
![]() $\mathsf {KM}$
that have instances of Comprehension of ever growing formula complexity, but in such a way that full
$\mathsf {KM}$
that have instances of Comprehension of ever growing formula complexity, but in such a way that full
![]() $\mathsf {KM}$
isn’t provable from those instances. This type of subsystem is hardly considered in the literature and for this reason it may require some novel treatment. The status of the same kind of the fragment of arithmetic and first-order set theory is also unknown. Additionally, while one may consider levels of formula complexity in the single scheme (induction) in arithmetic and (comprehension) in class theory, the same do not apply to
$\mathsf {KM}$
isn’t provable from those instances. This type of subsystem is hardly considered in the literature and for this reason it may require some novel treatment. The status of the same kind of the fragment of arithmetic and first-order set theory is also unknown. Additionally, while one may consider levels of formula complexity in the single scheme (induction) in arithmetic and (comprehension) in class theory, the same do not apply to
![]() $\mathsf {ZF}$
as one should also consider fragments of Replacement together with the full scheme of Separation, or other natural systems like Zermelo set theory plus the assertion that every set is in a
$\mathsf {ZF}$
as one should also consider fragments of Replacement together with the full scheme of Separation, or other natural systems like Zermelo set theory plus the assertion that every set is in a
![]() $\mathrm {V}_\alpha $
. Therefore, while the picture may be said to be nearly complete for
$\mathrm {V}_\alpha $
. Therefore, while the picture may be said to be nearly complete for
![]() $\mathsf {KM}$
,
$\mathsf {KM}$
,
![]() $\mathsf {PA}$
, and
$\mathsf {PA}$
, and
![]() $\mathsf {Z}_2$
, there is still a lot to be discovered with respect to
$\mathsf {Z}_2$
, there is still a lot to be discovered with respect to
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Acknowledgment
We thank the anonymous referee for their comments.
Funding
This research was supported by FCT through CIDMA and projects UIDB/04106/2020 and UIDP/04106/2020.