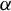1. Introduction and statement of results
In his book on thermodynamic formalism [Reference RuelleRue04], Ruelle introduced the concept of Smale spaces, which intended to axiomatically generalize the concept of a smooth hyperbolic map to the setting of compact metric spaces. This general framework was a unified theory under which many types of chaotic systems could be included. Some of the systems included under this umbrella are Anosov systems, basic sets of Axiom A systems, mixing shifts of finite type, hyperbolic toral automorphisms, etc. One of the many features shared by these systems is the existence of stable and unstable sets, generalizing the concept of stable and unstable manifolds found in some smooth systems. Later, Wieler [Reference WielerWie14] characterized Smale spaces with zero-dimensional stable sets as inverse limits satisfying certain conditions.
This paper studies various aspects of inverse limits of locally expanding affine linear maps on flat branched manifolds, which I call flat Wieler solenoids since they are a subclass of the types of Smale spaces classified by Wieler. They are spaces which are in a sense of intermediate type: on one extreme, Anosov maps are defined on smooth manifolds whereas mixing subshifts of finite type are defined on totally disconnected sets. Flat Wieler solenoids lie somewhere between these two extremes and it is this intermediate position that makes them particularly interesting. Although this is a subclass of Wieler’s more general classification, it is a class with a lot of rich examples. In particular, it includes the tiling spaces of self-similar tilings, or tilings built using a substitution rule. They are also related to primitive substitution systems in symbolic dynamics.
Let me be more precise (all the following terms are defined in §2): let
![]() $\Gamma $
be a flat branched manifold of dimension
$\Gamma $
be a flat branched manifold of dimension
![]() $d>0$
and
$d>0$
and
![]() $\gamma :\Gamma \rightarrow \Gamma $
be a locally expanding affine linear map. This means that
$\gamma :\Gamma \rightarrow \Gamma $
be a locally expanding affine linear map. This means that
![]() $\gamma $
has constant derivative
$\gamma $
has constant derivative
![]() $D_\gamma \in GL(d,\mathbb {R})$
outside the branch points of
$D_\gamma \in GL(d,\mathbb {R})$
outside the branch points of
![]() $\Gamma $
, with smallest eigenvalue
$\Gamma $
, with smallest eigenvalue
![]() $\unicode{x3bb} _0$
satisfying
$\unicode{x3bb} _0$
satisfying
![]() $|\unicode{x3bb} _0|>1$
. The inverse limit of the pair
$|\unicode{x3bb} _0|>1$
. The inverse limit of the pair
![]() $(\Gamma ,\gamma )$
is
$(\Gamma ,\gamma )$
is
This is a flat Wieler solenoid. It has a local product structure of the form
![]() $B_{\varepsilon }\times \mathcal {C}$
, where
$B_{\varepsilon }\times \mathcal {C}$
, where
![]() $B_{\varepsilon }$
is the
$B_{\varepsilon }$
is the
![]() $\varepsilon $
-ball of dimension d and
$\varepsilon $
-ball of dimension d and
![]() $\mathcal {C}$
is a Cantor set. It becomes a Smale space when paired with the ‘hyperbolic’ map
$\mathcal {C}$
is a Cantor set. It becomes a Smale space when paired with the ‘hyperbolic’ map
![]() $\Phi :\Omega _\gamma \rightarrow \Omega _\gamma $
defined by applying
$\Phi :\Omega _\gamma \rightarrow \Omega _\gamma $
defined by applying
![]() $\gamma $
to every coordinate of
$\gamma $
to every coordinate of
![]() $z\in \Omega _\gamma $
. Under this map, the Cantor sets in the local structure become stable sets and the Euclidean components become the unstable sets. Under suitable conditions,
$z\in \Omega _\gamma $
. Under this map, the Cantor sets in the local structure become stable sets and the Euclidean components become the unstable sets. Under suitable conditions,
![]() $\Omega _\gamma $
is a foliated space with each leaf dense in
$\Omega _\gamma $
is a foliated space with each leaf dense in
![]() $\Omega _\gamma $
and homeomorphic to
$\Omega _\gamma $
and homeomorphic to
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
Although
![]() $\Omega _\gamma $
is not a manifold, it still has a rich topological and geometric structure. First, the Čech cohomology can be computed as the direct limit of the cohomologies of
$\Omega _\gamma $
is not a manifold, it still has a rich topological and geometric structure. First, the Čech cohomology can be computed as the direct limit of the cohomologies of
![]() $\Gamma $
under the induced map
$\Gamma $
under the induced map
![]() $\gamma ^{*}$
. Another way to recover this topological information, à la de Rham, is to consider the set of functions with the highest possible regularity on
$\gamma ^{*}$
. Another way to recover this topological information, à la de Rham, is to consider the set of functions with the highest possible regularity on
![]() $\Omega $
, consider differential forms with coefficients in this space of functions, and then compute the cohomology of this complex of forms defined by the natural leafwise de Rham differential operator [Reference Kellendonk and PutnamKP06]. The space of functions which serves this role are the leafwise
$\Omega $
, consider differential forms with coefficients in this space of functions, and then compute the cohomology of this complex of forms defined by the natural leafwise de Rham differential operator [Reference Kellendonk and PutnamKP06]. The space of functions which serves this role are the leafwise
![]() $C^\infty $
, transversally locally constant functions, denoted by
$C^\infty $
, transversally locally constant functions, denoted by
![]() $C^\infty _{tlc}(\Omega )$
. These functions have the highest regularity in the smooth direction (
$C^\infty _{tlc}(\Omega )$
. These functions have the highest regularity in the smooth direction (
![]() $C^\infty $
) as well as the highest regularity in the transverse, totally disconnected direction (locally constant).
$C^\infty $
) as well as the highest regularity in the transverse, totally disconnected direction (locally constant).
One of the motivations behind the paper is a lack of good spaces of functions on
![]() $\Omega _\gamma $
of intermediate regularity. The usual tricks afforded by Sobolev spaces on smooth manifolds are not immediately available in this setting since it is not clear how they can afford an accounting of the regularity of a function in the totally disconnected direction. I propose that looking at the Hölder regularity in the totally disconnected direction can get us started in working with spaces of functions with intermediate regularity. Unlike Euclidean spaces, the space of
$\Omega _\gamma $
of intermediate regularity. The usual tricks afforded by Sobolev spaces on smooth manifolds are not immediately available in this setting since it is not clear how they can afford an accounting of the regularity of a function in the totally disconnected direction. I propose that looking at the Hölder regularity in the totally disconnected direction can get us started in working with spaces of functions with intermediate regularity. Unlike Euclidean spaces, the space of
![]() $\alpha $
-Hölder functions on a Cantor set is non-trivial for all
$\alpha $
-Hölder functions on a Cantor set is non-trivial for all
![]() $\alpha>0$
and thus
$\alpha>0$
and thus
![]() $\alpha $
-Hölder functions do supplant the notion of regularity in this setting.
$\alpha $
-Hölder functions do supplant the notion of regularity in this setting.
To get a grasp on a good space of smooth functions on
![]() $\Omega $
, in §2.1, I define the set
$\Omega $
, in §2.1, I define the set
![]() $\mathcal {S}^r_{\alpha }$
of functions on
$\mathcal {S}^r_{\alpha }$
of functions on
![]() $\Omega $
which are roughly described as functions which are
$\Omega $
which are roughly described as functions which are
![]() $C^r$
in the leaf direction and
$C^r$
in the leaf direction and
![]() $\alpha $
-Hölder in the transverse direction. This is how one can handle different degrees of regularity in the smooth and non-smooth directions of the space
$\alpha $
-Hölder in the transverse direction. This is how one can handle different degrees of regularity in the smooth and non-smooth directions of the space
![]() $\Omega $
. It will be shown that
$\Omega $
. It will be shown that
![]() $\mathcal {S}^r_{\alpha }$
is, in a sense, dense in the space
$\mathcal {S}^r_{\alpha }$
is, in a sense, dense in the space
![]() $C^r_{\alpha }$
of leafwise
$C^r_{\alpha }$
of leafwise
![]() $C^r$
functions which are
$C^r$
functions which are
![]() $\alpha $
-Hölder in the transverse direction up to r derivatives.
$\alpha $
-Hölder in the transverse direction up to r derivatives.
The concept of
![]() $\alpha $
-Hölder functions implicitly makes reference to a metric on
$\alpha $
-Hölder functions implicitly makes reference to a metric on
![]() $\Omega $
and so a function which is
$\Omega $
and so a function which is
![]() $\alpha $
-Hölder in one metric may be
$\alpha $
-Hölder in one metric may be
![]() $\alpha '$
-Hölder in another metric for some
$\alpha '$
-Hölder in another metric for some
![]() $\alpha '\neq \alpha $
. In these types of spaces, there is a natural metric in reference to which all statements will be made. One of the properties of this metric is that, for any leafwise first-order differential operator
$\alpha '\neq \alpha $
. In these types of spaces, there is a natural metric in reference to which all statements will be made. One of the properties of this metric is that, for any leafwise first-order differential operator
![]() $\partial $
and
$\partial $
and
![]() $f\in \mathcal {S}^r_{\alpha }$
, the derivative satisfies
$f\in \mathcal {S}^r_{\alpha }$
, the derivative satisfies
![]() $\partial f \in \mathcal {S}^{r-1}_{\alpha +1}$
. In other words, leafwise differentiation reduces leafwise regularity, but increases transverse regularity. It seems to me like this has gone unnoticed, and there is much to gain from this observation.
$\partial f \in \mathcal {S}^{r-1}_{\alpha +1}$
. In other words, leafwise differentiation reduces leafwise regularity, but increases transverse regularity. It seems to me like this has gone unnoticed, and there is much to gain from this observation.
Let
![]() $H^{*}_{r,\alpha }$
be the cohomology of the complex of leafwise smooth forms with coefficients in
$H^{*}_{r,\alpha }$
be the cohomology of the complex of leafwise smooth forms with coefficients in
![]() $\mathcal {S}^r_{\alpha }$
. The first result gives a lower bound on the regularity of functions in this complex, above which the usual real cohomology of
$\mathcal {S}^r_{\alpha }$
. The first result gives a lower bound on the regularity of functions in this complex, above which the usual real cohomology of
![]() $\Omega $
can be recovered.
$\Omega $
can be recovered.
Theorem 1.1. Let
![]() $\Omega $
be a flat Wieler solenoid and
$\Omega $
be a flat Wieler solenoid and
![]() $H^{*}_{r,\alpha }(\Omega )$
the cohomology of tangential forms on
$H^{*}_{r,\alpha }(\Omega )$
the cohomology of tangential forms on
![]() $\Omega $
with coefficients in
$\Omega $
with coefficients in
![]() $\mathcal {S}^r_{\alpha }(\Omega )$
. If
$\mathcal {S}^r_{\alpha }(\Omega )$
. If
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>1$
, then
$\alpha>1$
, then
This theorem should remind one of de Rham regularization. Indeed, part of the proof uses de Rham regularization (to find bounds for r). However, more needs to be done to ensure that
![]() $\alpha>1$
guarantees that the cohomology is finite dimensional. The first immediate application of this theorem is for the speed of ergodicity of functions in
$\alpha>1$
guarantees that the cohomology is finite dimensional. The first immediate application of this theorem is for the speed of ergodicity of functions in
![]() $\mathcal {S}^r_{\alpha }$
for
$\mathcal {S}^r_{\alpha }$
for
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>1$
. This essentially follows from the arguments in [Reference Schmieding and TreviñoST18] and it is discussed in §3.1. It improves previous results on deviations of ergodic integrals in that it increases the set of functions for which the deviation results hold.
$\alpha>1$
. This essentially follows from the arguments in [Reference Schmieding and TreviñoST18] and it is discussed in §3.1. It improves previous results on deviations of ergodic integrals in that it increases the set of functions for which the deviation results hold.
As mentioned above, there is a self-homeomorphism
![]() $\Phi :\Omega _\gamma \rightarrow \Omega _\gamma $
which makes a flat Wieler solenoid a Smale space. This map preserves an absolutely continuous probability measure
$\Phi :\Omega _\gamma \rightarrow \Omega _\gamma $
which makes a flat Wieler solenoid a Smale space. This map preserves an absolutely continuous probability measure
![]() $\mu $
and is topologically mixing [Reference Anderson and PutnamAP98, Proposition 3.1]. The second application of the careful study of transverse Hölder regularity is to the speed of mixing of the map
$\mu $
and is topologically mixing [Reference Anderson and PutnamAP98, Proposition 3.1]. The second application of the careful study of transverse Hölder regularity is to the speed of mixing of the map
![]() $\Phi :\Omega \rightarrow \Omega $
. To do this, the notion of the Ruelle spectrum has to be defined.
$\Phi :\Omega \rightarrow \Omega $
. To do this, the notion of the Ruelle spectrum has to be defined.
Definition 1.2. Let
![]() $\Phi :\Omega \rightarrow \Omega $
be a map preserving a probability measure
$\Phi :\Omega \rightarrow \Omega $
be a map preserving a probability measure
![]() $\mu $
and
$\mu $
and
![]() $\mathcal {F}$
a space of bounded functions on
$\mathcal {F}$
a space of bounded functions on
![]() $\Omega $
. Let I be a finite or countable set,
$\Omega $
. Let I be a finite or countable set,
![]() $\Lambda = \{\unicode{x3bb} _i\}_{i\in I}$
a set of complex numbers with
$\Lambda = \{\unicode{x3bb} _i\}_{i\in I}$
a set of complex numbers with
![]() $|\unicode{x3bb} _i|\in (0,1]$
such that for any
$|\unicode{x3bb} _i|\in (0,1]$
such that for any
![]() $\varepsilon>0$
, there are only finitely many i such that
$\varepsilon>0$
, there are only finitely many i such that
![]() $|\unicode{x3bb} _i|>\varepsilon $
, and let
$|\unicode{x3bb} _i|>\varepsilon $
, and let
![]() $\{N_i\}_{i\in I}$
be non-negative integers. Then
$\{N_i\}_{i\in I}$
be non-negative integers. Then
![]() $\Phi $
has Ruelle spectrum
$\Phi $
has Ruelle spectrum
![]() $\Lambda $
with Jordan block dimension
$\Lambda $
with Jordan block dimension
![]() $\{N_i\}$
on
$\{N_i\}$
on
![]() $\mathcal {F}$
if, for any
$\mathcal {F}$
if, for any
![]() $f,g\in \mathcal {F}$
and
$f,g\in \mathcal {F}$
and
![]() $\varepsilon>0$
, there is an asymptotic expansion
$\varepsilon>0$
, there is an asymptotic expansion

where
![]() $c_{i,j}(f,g)$
are non-zero bilinear functions of f and g of finite rank.
$c_{i,j}(f,g)$
are non-zero bilinear functions of f and g of finite rank.
Note that these asymptotics give precise information on the rates of mixing. Moreover, if
![]() $f\in \mathcal {F}$
is an eigenfunction for
$f\in \mathcal {F}$
is an eigenfunction for
![]() $\Phi $
with eigenvalue
$\Phi $
with eigenvalue
![]() $\nu $
and the essential spectrum for
$\nu $
and the essential spectrum for
![]() $\Phi ^{*}$
is reduced to
$\Phi ^{*}$
is reduced to
![]() $\{0\}$
, then
$\{0\}$
, then
![]() $\nu \in \Lambda $
. Thus, the search for the Ruelle spectrum reduces to the search of generalized eigenfunctions for the pullback operator defined by
$\nu \in \Lambda $
. Thus, the search for the Ruelle spectrum reduces to the search of generalized eigenfunctions for the pullback operator defined by
![]() $\Phi $
, called the transfer operator
$\Phi $
, called the transfer operator
![]() $\mathcal {L} = \Phi ^{*}$
, on a good space of functions
$\mathcal {L} = \Phi ^{*}$
, on a good space of functions
![]() $\mathcal {F}$
. To find a good
$\mathcal {F}$
. To find a good
![]() $\mathcal {F}$
, the use of the so-called anisotropic Banach spaces will be employed.
$\mathcal {F}$
, the use of the so-called anisotropic Banach spaces will be employed.
Computing the Ruelle spectra of systems has become fashionable in the last half-decade, especially through the use of anisotropic Banach spaces. In [Reference Faure, Gouëzel and LanneauFGL19], using transfer operator techniques and anisotropic Banach spaces, the authors noticed that the Ruelle spectrum for linear pseudo-Anosov maps on Riemann surfaces is composed entirely from cohomological information. Using different techniques, this was soon reproved in [Reference ForniFor22a], and that point of view was extended to the case of nonlinear pseudo-Anosov actions on surfaces [Reference ForniFor22b]. Those works were followed by [Reference Butterley, Kiamari and LiveraniBKL22] and the recent PhD dissertation of D. Galli—both using transfer operators and anisotropic Banach spaces—where the focus has been to extract resonances from the cohomology spectrum in a larger class of nonlinear systems. They concluded that the Ruelle spectrum contains cohomological information, but is not necessarily made up exclusively of cohomological information. The results here are of that type.
I will define anisotropic Banach spaces
![]() $\mathcal {B}^{r,\alpha }_m$
as the completion of the space of tangential m-forms with coefficients in
$\mathcal {B}^{r,\alpha }_m$
as the completion of the space of tangential m-forms with coefficients in
![]() $\mathcal {S}_{\alpha }^r$
with respect to an anisotropic norm, and then study the spectrum of the transfer operator on these spaces. The spaces of functions for which part of the Ruelle spectrum can be identified will be
$\mathcal {S}_{\alpha }^r$
with respect to an anisotropic norm, and then study the spectrum of the transfer operator on these spaces. The spaces of functions for which part of the Ruelle spectrum can be identified will be
![]() $\mathcal {B}_0^{\infty ,\alpha } = \bigcap _{r>0}\mathcal {B}_0^{r,\alpha }$
for
$\mathcal {B}_0^{\infty ,\alpha } = \bigcap _{r>0}\mathcal {B}_0^{r,\alpha }$
for
![]() $\alpha $
large enough.
$\alpha $
large enough.
Let
![]() $h_{\mathrm {top}}$
be the topological entropy of
$h_{\mathrm {top}}$
be the topological entropy of
![]() $\gamma :\Gamma \rightarrow \Gamma $
and
$\gamma :\Gamma \rightarrow \Gamma $
and
![]() $\chi _-$
the smallest Lyapunov exponent of
$\chi _-$
the smallest Lyapunov exponent of
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\sigma ^-$
be the set of eigenvalues
$\sigma ^-$
be the set of eigenvalues
![]() $\nu $
of
$\nu $
of
![]() $\Phi ^{-1*}:\check H^d(\Omega ;\mathbb {R})\rightarrow \check H^d(\Omega ;\mathbb {R})$
which satisfy
$\Phi ^{-1*}:\check H^d(\Omega ;\mathbb {R})\rightarrow \check H^d(\Omega ;\mathbb {R})$
which satisfy
![]() $\log |\nu |< \chi _- - h_{\mathrm {top}}$
. Note that when
$\log |\nu |< \chi _- - h_{\mathrm {top}}$
. Note that when
![]() $d=1$
, this is the set of all contracting eigenvalues.
$d=1$
, this is the set of all contracting eigenvalues.
Theorem 1.3. Let
![]() $\Phi :\Omega \rightarrow \Omega $
be the topologically mixing map on the solenoid which preserves the absolutely continuous probability measure
$\Phi :\Omega \rightarrow \Omega $
be the topologically mixing map on the solenoid which preserves the absolutely continuous probability measure
![]() $\mu $
. For
$\mu $
. For
![]() $\alpha> {h_{\mathrm {top}}}/{\chi _-}$
and
$\alpha> {h_{\mathrm {top}}}/{\chi _-}$
and
![]() $r\in \mathbb {N}$
, the following hold.
$r\in \mathbb {N}$
, the following hold.
-
(i) If
 $d=1$
, then the set of eigenvalues for
$d=1$
, then the set of eigenvalues for
 $\mathcal {L} = \Phi ^{-1*}$
acting on
$\mathcal {L} = \Phi ^{-1*}$
acting on
 $\mathcal {B}_0^{r,\alpha }$
contains
$\mathcal {B}_0^{r,\alpha }$
contains
 $\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
. In addition, if
$\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
. In addition, if
 $\nu $
is an eigenvalue in
$\nu $
is an eigenvalue in
 $\mathcal {B}_0^{r,\alpha }$
and
$\mathcal {B}_0^{r,\alpha }$
and
 $k<\alpha - ({h_{\mathrm {top}}}/{\chi _-})$
, then
$k<\alpha - ({h_{\mathrm {top}}}/{\chi _-})$
, then
 $e^{-kh_{\mathrm {top}}}\nu $
is an eigenvalue in
$e^{-kh_{\mathrm {top}}}\nu $
is an eigenvalue in
 $\mathcal {B}_0^{r+k,\alpha -k}$
. It follows that if
$\mathcal {B}_0^{r+k,\alpha -k}$
. It follows that if
 $\mathcal {F}:= \bigcap \nolimits _{\alpha>0,r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
$\mathcal {F}:= \bigcap \nolimits _{\alpha>0,r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
 $\mathcal {F}$
contains the set of numbers of the form
$\mathcal {F}$
contains the set of numbers of the form
 $e^{-kh_{\mathrm {top}}}\nu $
with
$e^{-kh_{\mathrm {top}}}\nu $
with
 $\nu \in \sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
and
$\nu \in \sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
and
 $k\in \mathbb {N}$
;
$k\in \mathbb {N}$
; -
(ii) If
 $d=2$
, then the set of eigenvalues for
$d=2$
, then the set of eigenvalues for
 $\mathcal {L} = \Phi ^{-1*}$
acting on
$\mathcal {L} = \Phi ^{-1*}$
acting on
 $\mathcal {B}_0^{r,\alpha }$
contains
$\mathcal {B}_0^{r,\alpha }$
contains
 $\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
. If
$\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
. If
 $\mathcal {S}^{\infty }_{\alpha }:= \bigcap _{r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
$\mathcal {S}^{\infty }_{\alpha }:= \bigcap _{r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
 $\mathcal {S}^{\infty }_{\alpha }$
contains the set
$\mathcal {S}^{\infty }_{\alpha }$
contains the set
 $\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
.
$\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
.
Remark 1.4. Some remarks.
-
(i) Since the tiling spaces of self-similar tilings are flat Wieler solenoids [Reference Anderson and PutnamAP98] of this type, Theorem 1.3 gives the rate if mixing of the substitution rule on these spaces. This can be interpreted as the rates of decay of correlations of the different scales of the tiling.
-
(ii) Let me connect the one-dimensional case with the Pisot conjecture. The hypotheses of the homological Pisot conjecture assert that
 $\sigma ^-_1\setminus \{e^{-h_{\mathrm {top}}}\}=\varnothing $
(see the survey [Reference Akiyama, Barge, Berthé, Lee, Siegel, Kellendonk, Lenz and SavinienABB+15]). Thus, under the hypothesis of the homological Pisot conjecture, I find no obstruction to having super exponential decay of correlations, which is a feature of algebraic systems. Thus, showing that
$\sigma ^-_1\setminus \{e^{-h_{\mathrm {top}}}\}=\varnothing $
(see the survey [Reference Akiyama, Barge, Berthé, Lee, Siegel, Kellendonk, Lenz and SavinienABB+15]). Thus, under the hypothesis of the homological Pisot conjecture, I find no obstruction to having super exponential decay of correlations, which is a feature of algebraic systems. Thus, showing that
 $\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
is the entire spectrum would be very valuable.
$\sigma ^-\setminus \{e^{-h_{\mathrm {top}}}\}$
is the entire spectrum would be very valuable. -
(iii) Examples of two-dimensional solenoids for which
 $\sigma ^-_1\setminus \{e^{-h_{\mathrm {top}}}\}\neq \varnothing $
include the tiling spaces of self-similar tilings which are weakly mixing under the translation action along leaves, such as the Godrèche–Lançon–Billard tiling and one of Danzer’s sevenfold tilings. See [Reference Baake and GrimmBG13, §6.5] for more details.
$\sigma ^-_1\setminus \{e^{-h_{\mathrm {top}}}\}\neq \varnothing $
include the tiling spaces of self-similar tilings which are weakly mixing under the translation action along leaves, such as the Godrèche–Lançon–Billard tiling and one of Danzer’s sevenfold tilings. See [Reference Baake and GrimmBG13, §6.5] for more details.
Finally, another application of the study of transverse Hölder regularity in these spaces is to the solution of the cohomological equation in the setting of primitive substitution subshifts. Let
![]() $\mathcal {A}$
be a finite set and let
$\mathcal {A}$
be a finite set and let
![]() $\varrho $
be a primitive substitution rule on
$\varrho $
be a primitive substitution rule on
![]() $\mathcal {A}$
(all of these terms are defined in §5). Let
$\mathcal {A}$
(all of these terms are defined in §5). Let
![]() $\sigma :X_{\varrho }\rightarrow X_{\varrho }$
be the minimal subshift defined by this substitution rule. Let
$\sigma :X_{\varrho }\rightarrow X_{\varrho }$
be the minimal subshift defined by this substitution rule. Let
![]() $H_{\alpha }(X_{\varrho })$
be the space of
$H_{\alpha }(X_{\varrho })$
be the space of
![]() $\alpha $
-Hölder functions on
$\alpha $
-Hölder functions on
![]() $X_{\varrho }$
(this is with respect to some natural ultrametric; the following results are stated with respect to a specific, natural ultrametric). Let
$X_{\varrho }$
(this is with respect to some natural ultrametric; the following results are stated with respect to a specific, natural ultrametric). Let
![]() $H^0_{\alpha }(X_{\varrho })$
be the quotient of
$H^0_{\alpha }(X_{\varrho })$
be the quotient of
![]() $H_{\alpha }(X_{\varrho })$
with respect to the equivalence relation
$H_{\alpha }(X_{\varrho })$
with respect to the equivalence relation
![]() $f\sim g$
if there exists a
$f\sim g$
if there exists a
![]() $u\in H_{\alpha -2}(X_{\varrho })$
such that
$u\in H_{\alpha -2}(X_{\varrho })$
such that
![]() $f-g = u\circ \sigma - u$
. This is the
$f-g = u\circ \sigma - u$
. This is the
![]() $\alpha $
-Hölder cohomology of
$\alpha $
-Hölder cohomology of
![]() $X_{\varrho }$
.
$X_{\varrho }$
.
Theorem 1.5. Let
![]() $\mathcal {A}$
be a finite set and let
$\mathcal {A}$
be a finite set and let
![]() $\varrho $
be a primitive substitution rule on
$\varrho $
be a primitive substitution rule on
![]() $\mathcal {A}$
. If
$\mathcal {A}$
. If
![]() $\alpha>2$
, then
$\alpha>2$
, then
![]() $H^0_{\alpha }(X_{\varrho })$
is finite dimensional. That is, if
$H^0_{\alpha }(X_{\varrho })$
is finite dimensional. That is, if
![]() $\alpha>2$
, there are finitely many obstructions to finding a solution
$\alpha>2$
, there are finitely many obstructions to finding a solution
![]() $u\in H_{\alpha -2}(X_{\varrho })$
to the cohomological equation
$u\in H_{\alpha -2}(X_{\varrho })$
to the cohomological equation
![]() $f = u\circ \sigma -u$
for
$f = u\circ \sigma -u$
for
![]() $f\in H_{\alpha }(X_{\varrho })$
.
$f\in H_{\alpha }(X_{\varrho })$
.
Remark 1.6. Some remarks.
-
(i) The locally constant, integral cohomology has been thoroughly studied for minimal Cantor systems. More precisely, the structure of the set of equivalence classes of
 $C(X,\mathbb {Z})$
up to coboundaries is a fundamental invariant in the theory of orbit equivalence for Cantor minimal systems [Reference Giordano, Putnam and SkauGPS95]. However, as far as I know, the problem of solving the cohomological equation for varying degrees of regularity on Cantor sets has not been considered before.
$C(X,\mathbb {Z})$
up to coboundaries is a fundamental invariant in the theory of orbit equivalence for Cantor minimal systems [Reference Giordano, Putnam and SkauGPS95]. However, as far as I know, the problem of solving the cohomological equation for varying degrees of regularity on Cantor sets has not been considered before. -
(ii) The ideas leading up to the theorem above do not only hold for substitution systems. In fact, with the right use of Oseledets theorem, I expect the theorem above to hold for a large class of minimal Cantor systems, including a large class of so-called S-adic systems. This will be pursued in a future paper.
-
(iii) It is unclear whether a loss of regularity of order
 $2$
is optimal. Although a loss of 1 may be necessary, a loss of 2 may be a feature of the way the theorem is proved. I would like to see a proof of this statement which does not rely on embedding
$2$
is optimal. Although a loss of 1 may be necessary, a loss of 2 may be a feature of the way the theorem is proved. I would like to see a proof of this statement which does not rely on embedding
 $X_{\varrho }$
into a solenoid as it does here.
$X_{\varrho }$
into a solenoid as it does here.
This paper is organized as follows. Background material is covered in §2, including the function spaces
![]() $\mathcal {S}^r_{\alpha }$
, which, as far as I know, are new. Section 3 deals with proving that the
$\mathcal {S}^r_{\alpha }$
, which, as far as I know, are new. Section 3 deals with proving that the
![]() $r,\alpha $
cohomology is isomorphic to the usual real cohomologies (Theorem 1.1) for
$r,\alpha $
cohomology is isomorphic to the usual real cohomologies (Theorem 1.1) for
![]() $r,\alpha $
large enough. Section 4 is devoted to the study of the Ruelle spectrum: anisotropic Banach spaces of forms are introduced and the action of the transfer operator on them is studied leading to Theorem 1.3. Finally, in §5, the solutions of the cohomological equation on
$r,\alpha $
large enough. Section 4 is devoted to the study of the Ruelle spectrum: anisotropic Banach spaces of forms are introduced and the action of the transfer operator on them is studied leading to Theorem 1.3. Finally, in §5, the solutions of the cohomological equation on
![]() $X_{\varrho }$
are studied by relating them to solutions of the cohomological equation on one-dimensional solenoids, proving Theorem 1.5.
$X_{\varrho }$
are studied by relating them to solutions of the cohomological equation on one-dimensional solenoids, proving Theorem 1.5.
2. Wieler solenoids of flat branched manifolds
Let
![]() $\Gamma $
be a connected, flat branched manifold of dimension d. This means that
$\Gamma $
be a connected, flat branched manifold of dimension d. This means that
![]() $\Gamma $
is obtained by gluing several polytopes of dimension d along their faces in such a way that every k-dimensional face meets another of the same dimension. This branched manifold has a natural CW structure and flat metric; denote by
$\Gamma $
is obtained by gluing several polytopes of dimension d along their faces in such a way that every k-dimensional face meets another of the same dimension. This branched manifold has a natural CW structure and flat metric; denote by
![]() $I^k$
its
$I^k$
its
![]() $k\mathrm {th}$
-skeleton. Let B be the branching set, that is, the set of points x such that a small ball around x is not homeomorphic to an open Euclidean ball. If
$k\mathrm {th}$
-skeleton. Let B be the branching set, that is, the set of points x such that a small ball around x is not homeomorphic to an open Euclidean ball. If
![]() $B=\varnothing $
, then
$B=\varnothing $
, then
![]() $\Gamma $
is a manifold. The focus here will be on cases where
$\Gamma $
is a manifold. The focus here will be on cases where
![]() $B\neq \varnothing $
. Setting
$B\neq \varnothing $
. Setting
![]() $B_k := (I^k\setminus I^{k-1})\cap B$
, it is worth pointing out that every point on
$B_k := (I^k\setminus I^{k-1})\cap B$
, it is worth pointing out that every point on
![]() $B_k$
is a k-dimensional flat manifold and, as such, it has well-defined tangent and cotangent spaces.
$B_k$
is a k-dimensional flat manifold and, as such, it has well-defined tangent and cotangent spaces.
Let
![]() $\gamma :\Gamma \rightarrow \Gamma $
be a locally expanding and surjective map with constant compatible derivative. This means that the derivative map is non-singular and on
$\gamma :\Gamma \rightarrow \Gamma $
be a locally expanding and surjective map with constant compatible derivative. This means that the derivative map is non-singular and on
![]() $I^d\setminus I^{d-1}$
, the derivative
$I^d\setminus I^{d-1}$
, the derivative
![]() $D_\gamma $
can be identified with some
$D_\gamma $
can be identified with some
![]() $D_\gamma \in GL(d,\mathbb {R})$
. Let
$D_\gamma \in GL(d,\mathbb {R})$
. Let
![]() $\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d>1$
be the eigenvalues of
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d>1$
be the eigenvalues of
![]() $D_\gamma $
and set
$D_\gamma $
and set
![]() $\unicode{x3bb} _0 = \min _i|\unicode{x3bb} _i|$
and
$\unicode{x3bb} _0 = \min _i|\unicode{x3bb} _i|$
and
![]() $\unicode{x3bb} = \mathrm {det}\, D_\gamma $
.
$\unicode{x3bb} = \mathrm {det}\, D_\gamma $
.
The solenoid defined by
![]() $\gamma $
is the space
$\gamma $
is the space
It can also be defined as an inverse/projective limit: the inverse limit
can easily be seen to match the first definition. This is a flat Wieler solenoid since it is part of Wieler’s classification of Smale spaces with totally disconnected stable sets (this structure will be examined below). The
![]() $\gamma $
-solenoid comes equipped with a probability measure which is compatible with the inverse limit structure. To describe this more precisely, denote by
$\gamma $
-solenoid comes equipped with a probability measure which is compatible with the inverse limit structure. To describe this more precisely, denote by
![]() $\pi _k:\bar {z}\mapsto z_k$
the projection onto the
$\pi _k:\bar {z}\mapsto z_k$
the projection onto the
![]() $k\mathrm {th}$
coordinate, and denote by
$k\mathrm {th}$
coordinate, and denote by
![]() $\Gamma _k$
to be the
$\Gamma _k$
to be the
![]() $k\mathrm {th}$
copy of
$k\mathrm {th}$
copy of
![]() $\Gamma $
:
$\Gamma $
:
![]() $\Gamma _k = \pi _k(\Omega )$
. Let
$\Gamma _k = \pi _k(\Omega )$
. Let
![]() $\mu _k$
be the normalized Lebesgue measure on
$\mu _k$
be the normalized Lebesgue measure on
![]() $\Gamma _k$
induced from the flat metric. Since
$\Gamma _k$
induced from the flat metric. Since
![]() $\gamma $
preserves Lebesgue measure, it follows that
$\gamma $
preserves Lebesgue measure, it follows that
![]() $\gamma _*\mu _k = \mu _{k-1}$
. Thus, if we equip
$\gamma _*\mu _k = \mu _{k-1}$
. Thus, if we equip
![]() $\Omega $
with
$\Omega $
with
![]() $\mu := \otimes _k\mu _k$
, we have that
$\mu := \otimes _k\mu _k$
, we have that
![]() $\pi _{k*}\mu = \mu _k$
for every k.
$\pi _{k*}\mu = \mu _k$
for every k.
Two assumptions need to be made on the pair
![]() $(\Gamma ,\gamma )$
.
$(\Gamma ,\gamma )$
.
-
(i) The map
 $\gamma :\Gamma \rightarrow \Gamma $
is primitive: there exists a
$\gamma :\Gamma \rightarrow \Gamma $
is primitive: there exists a
 $K>0$
such that for any two faces
$K>0$
such that for any two faces
 $F_1,F_2\subset \Gamma $
, there is a point
$F_1,F_2\subset \Gamma $
, there is a point
 $x\in F_1$
such that
$x\in F_1$
such that
 $\gamma ^K(x)\in F_2$
.
$\gamma ^K(x)\in F_2$
. -
(ii) The map
 $\gamma :\Gamma \rightarrow \Gamma $
forces the border. Although I will not discuss what is meant here, an implication of this assumption will be pointed out below.
$\gamma :\Gamma \rightarrow \Gamma $
forces the border. Although I will not discuss what is meant here, an implication of this assumption will be pointed out below. -
(iii) The map
 $\gamma $
is recognizable: roughly speaking, all d-cells have distinct images.
$\gamma $
is recognizable: roughly speaking, all d-cells have distinct images.
The solenoid
![]() $\Omega $
has a local product structure of
$\Omega $
has a local product structure of
![]() $B_{\varepsilon }(0)\times \mathcal {C}$
, where
$B_{\varepsilon }(0)\times \mathcal {C}$
, where
![]() $B_{\varepsilon }(0)$
is an
$B_{\varepsilon }(0)$
is an
![]() $\varepsilon $
-ball in
$\varepsilon $
-ball in
![]() $\mathbb {R}^d$
and
$\mathbb {R}^d$
and
![]() $\mathcal {C}$
is a Cantor set. Indeed, if
$\mathcal {C}$
is a Cantor set. Indeed, if
![]() $z = (z_0,z_1,\ldots )\in \Omega $
, then points close to z come from either varying the
$z = (z_0,z_1,\ldots )\in \Omega $
, then points close to z come from either varying the
![]() $z_0$
coordinate by a small amount (this is parameterized by
$z_0$
coordinate by a small amount (this is parameterized by
![]() $B_{\varepsilon }$
) or by varying in
$B_{\varepsilon }$
) or by varying in
![]() $\pi _0^{-1}(z_0)$
, which amounts to picking one of (potentially several) points in
$\pi _0^{-1}(z_0)$
, which amounts to picking one of (potentially several) points in
![]() $\gamma ^{-1}(z_0)$
, then one of (potentially several) points in the
$\gamma ^{-1}(z_0)$
, then one of (potentially several) points in the
![]() $\gamma $
-preimage of that point, and so on. It follows that since
$\gamma $
-preimage of that point, and so on. It follows that since
![]() $\unicode{x3bb}>1$
, this sequence of choices naturally gives a Cantor set.
$\unicode{x3bb}>1$
, this sequence of choices naturally gives a Cantor set.
There are two complementary dynamical systems defined on
![]() $\Omega $
. First, there is a self-homeomorphism
$\Omega $
. First, there is a self-homeomorphism
![]() $\Phi :\Omega \rightarrow \Omega $
which preserves the special measure
$\Phi :\Omega \rightarrow \Omega $
which preserves the special measure
![]() $\mu $
. In coordinates, the map is defined by
$\mu $
. In coordinates, the map is defined by
which, by construction, preserves the measure
![]() $\mu $
. The inverse is obtained by deleting the first coordinate.
$\mu $
. The inverse is obtained by deleting the first coordinate.
For
![]() $z\in \Omega $
, define its
$z\in \Omega $
, define its
![]() $k\mathrm {th}$
transversal set as
$k\mathrm {th}$
transversal set as
The sets
![]() $C_0^{\perp }(x)$
are all ultrametric sets which will be endowed with the metric
$C_0^{\perp }(x)$
are all ultrametric sets which will be endowed with the metric
where
![]() $k(y,z)$
is the smallest integer i such that
$k(y,z)$
is the smallest integer i such that
![]() $y_i\neq z_i$
; equivalently, the smallest integer i such that
$y_i\neq z_i$
; equivalently, the smallest integer i such that
![]() $C_i^{\perp }(y)\neq C_i^{\perp }(z)$
. These transversal sets can be seen to be the local stable set of x: if
$C_i^{\perp }(y)\neq C_i^{\perp }(z)$
. These transversal sets can be seen to be the local stable set of x: if
![]() $y\in C_0^{\perp }(x)$
, then
$y\in C_0^{\perp }(x)$
, then
![]() $d(\Phi ^n(x), \Phi ^n(y))\rightarrow 0$
as
$d(\Phi ^n(x), \Phi ^n(y))\rightarrow 0$
as
![]() $n\rightarrow \infty $
. The local unstable sets can also be seen, in the coordinates
$n\rightarrow \infty $
. The local unstable sets can also be seen, in the coordinates
![]() $B_{\varepsilon }\times \mathcal {C}$
around z, to be the Euclidean balls
$B_{\varepsilon }\times \mathcal {C}$
around z, to be the Euclidean balls
![]() $B_{\varepsilon }\times \{c\}$
for
$B_{\varepsilon }\times \{c\}$
for
![]() $c\in \mathcal {C}$
.
$c\in \mathcal {C}$
.
Second, there is the
![]() $\mathbb {R}^d$
action on
$\mathbb {R}^d$
action on
![]() $\Omega $
given by translating along unstable sets. More precisely, for
$\Omega $
given by translating along unstable sets. More precisely, for
![]() $z\in \Omega $
with
$z\in \Omega $
with
![]() $z_0=\pi _0(z)$
not in a branch of
$z_0=\pi _0(z)$
not in a branch of
![]() $\Gamma $
and
$\Gamma $
and
![]() $t\in \mathbb {R}^d$
of small norm, the translation of
$t\in \mathbb {R}^d$
of small norm, the translation of
![]() $z = (z_0,z_1,z_2,\ldots )$
by t is
$z = (z_0,z_1,z_2,\ldots )$
by t is
which is seen to preserve the condition in equation (1). The assumption that
![]() $(\Gamma ,\gamma )$
forces the border implies that this extends to an action of
$(\Gamma ,\gamma )$
forces the border implies that this extends to an action of
![]() $\mathbb {R}^d$
on
$\mathbb {R}^d$
on
![]() $\Omega $
; the primitivity condition implies that this action is minimal, that is, every orbit is dense. Finally, the recognizability condition implies that the action is free and so every orbit is homeomorphic to
$\Omega $
; the primitivity condition implies that this action is minimal, that is, every orbit is dense. Finally, the recognizability condition implies that the action is free and so every orbit is homeomorphic to
![]() $\mathbb {R}^d$
. Under these conditions, the action of
$\mathbb {R}^d$
. Under these conditions, the action of
![]() $\mathbb {R}^d$
is uniquely ergodic [Reference SolomyakSol97, Theorem 3.1], where the unique invariant probability measure is
$\mathbb {R}^d$
is uniquely ergodic [Reference SolomyakSol97, Theorem 3.1], where the unique invariant probability measure is
![]() $\mu $
.
$\mu $
.
Since the solenoid
![]() $\Omega $
has a local product structure of
$\Omega $
has a local product structure of
![]() $B_{\varepsilon }(0)\times C_k^{\perp }(x)$
, where
$B_{\varepsilon }(0)\times C_k^{\perp }(x)$
, where
![]() $B_{\varepsilon }(0)$
is an
$B_{\varepsilon }(0)$
is an
![]() $\varepsilon $
-ball, the
$\varepsilon $
-ball, the
![]() $\Phi $
-invariant measure
$\Phi $
-invariant measure
![]() $\mu $
has a local product structure of
$\mu $
has a local product structure of
![]() $\mbox {Leb}\times \nu _{x,k}$
, where
$\mbox {Leb}\times \nu _{x,k}$
, where
![]() $\mbox {Leb}$
is Lebesgue measure and
$\mbox {Leb}$
is Lebesgue measure and
![]() $\nu _{x,k}$
is a measure on a local transversal
$\nu _{x,k}$
is a measure on a local transversal
![]() $C_k^{\perp }(x)$
. This measure assigns to each local transversal
$C_k^{\perp }(x)$
. This measure assigns to each local transversal
![]() $C^{\perp }_k(x)$
the measure
$C^{\perp }_k(x)$
the measure
![]() $\nu _{x,k}(C_k^{\perp }(x))$
. Since
$\nu _{x,k}(C_k^{\perp }(x))$
. Since
![]() $\{\nu _{x,k}\}$
forms a system of transverse invariant measures for the
$\{\nu _{x,k}\}$
forms a system of transverse invariant measures for the
![]() $\mathbb {R}^d$
action in the sense of [Reference Bowen and MarcusBM77], they will all be denoted by
$\mathbb {R}^d$
action in the sense of [Reference Bowen and MarcusBM77], they will all be denoted by
![]() $\nu $
unless not doing so leads to ambiguity. Define
$\nu $
unless not doing so leads to ambiguity. Define
Lemma 2.1. There exists a
![]() $C_\mu>1$
such that for any
$C_\mu>1$
such that for any
![]() $x\in \Omega $
and
$x\in \Omega $
and
![]() $k\in \mathbb {N}_0$
,
$k\in \mathbb {N}_0$
,
Proof. Since
![]() $\Phi $
preserves
$\Phi $
preserves
![]() $\mu $
,
$\mu $
,
![]() $\mu $
has local product structure
$\mu $
has local product structure
![]() $\mathrm {Leb}\times \nu $
, and the Lebesgue measure scales as
$\mathrm {Leb}\times \nu $
, and the Lebesgue measure scales as
![]() $\unicode{x3bb} = \mathrm {det}(D_\gamma ) = \prod \unicode{x3bb} _i$
under
$\unicode{x3bb} = \mathrm {det}(D_\gamma ) = \prod \unicode{x3bb} _i$
under
![]() $\Phi $
,
$\Phi $
,
![]() $\nu $
scales as
$\nu $
scales as
![]() $\unicode{x3bb} ^{-1}$
under
$\unicode{x3bb} ^{-1}$
under
![]() $\Phi $
. So it follows that
$\Phi $
. So it follows that
![]() $\nu (C_1^{\perp }(x)) = \nu (\Phi (C_0^{\perp }(\Phi ^{-1}(x)))) = \unicode{x3bb} ^{-1}\nu (C_0^{\perp }(\Phi ^{-1}(x)))$
. By compactness, there are finitely many values of
$\nu (C_1^{\perp }(x)) = \nu (\Phi (C_0^{\perp }(\Phi ^{-1}(x)))) = \unicode{x3bb} ^{-1}\nu (C_0^{\perp }(\Phi ^{-1}(x)))$
. By compactness, there are finitely many values of
![]() $\nu (C_0^{\perp }(\Phi ^{-1}(x)))$
, and so iterating the calculation gives the desired bound.
$\nu (C_0^{\perp }(\Phi ^{-1}(x)))$
, and so iterating the calculation gives the desired bound.
2.1. Function spaces
Let
![]() $C^r(\Gamma )$
be the space of functions on the branched manifold which are
$C^r(\Gamma )$
be the space of functions on the branched manifold which are
![]() $C^r$
smooth at the branch set. More precisely, let
$C^r$
smooth at the branch set. More precisely, let
![]() $i_k:B_k\rightarrow \Gamma $
be the inclusion of the
$i_k:B_k\rightarrow \Gamma $
be the inclusion of the
![]() $k\mathrm {th}$
-dimensional part of the branched set. A first order differential operator X on
$k\mathrm {th}$
-dimensional part of the branched set. A first order differential operator X on
![]() $\Gamma $
is one for which there exists a first order differential operator
$\Gamma $
is one for which there exists a first order differential operator
![]() $X_k$
on
$X_k$
on
![]() $B_k$
which can be extended to X on
$B_k$
which can be extended to X on
![]() $\Gamma $
, that is, so that
$\Gamma $
, that is, so that
![]() $X_k i^{*}_k (f) = i_k^{*}(Xf)$
for all k. In other words,
$X_k i^{*}_k (f) = i_k^{*}(Xf)$
for all k. In other words,
![]() $C^r(\Gamma )$
is the set of functions
$C^r(\Gamma )$
is the set of functions
![]() $f\in C^r(\Gamma )$
such that
$f\in C^r(\Gamma )$
such that

for some
![]() $X_k$
and for all
$X_k$
and for all
![]() $k>0$
. Thus, a first order differential operator X can be identified with a d-tuple
$k>0$
. Thus, a first order differential operator X can be identified with a d-tuple
![]() $\{X_1,\ldots , X_d\}$
of first order differential operators, where
$\{X_1,\ldots , X_d\}$
of first order differential operators, where
![]() $X_k$
on
$X_k$
on
![]() $B_k$
satisfies equation (5).
$B_k$
satisfies equation (5).
Another way to characterize
![]() $C^r(\Gamma )$
is as follows: since
$C^r(\Gamma )$
is as follows: since
![]() $\mathbb {R}^d$
acts on
$\mathbb {R}^d$
acts on
![]() $\Omega $
by translation along unstable leaves, any
$\Omega $
by translation along unstable leaves, any
![]() $v\in \mathbb {R}^d$
defines the leafwise differential operators
$v\in \mathbb {R}^d$
defines the leafwise differential operators
![]() $\partial _{v}$
as
$\partial _{v}$
as
Let
![]() $C^r(\Omega )$
be the set of leafwise-
$C^r(\Omega )$
be the set of leafwise-
![]() $C^r$
functions on
$C^r$
functions on
![]() $\Omega $
with respect to the family of operators
$\Omega $
with respect to the family of operators
![]() $\partial _{e_1},\ldots , \partial _{e_d}$
. Thus,
$\partial _{e_1},\ldots , \partial _{e_d}$
. Thus,
![]() $f\in C^r(\Gamma _k)$
if and only if
$f\in C^r(\Gamma _k)$
if and only if
![]() $\pi ^{*}_kf\in C^r(\Omega )$
. Let
$\pi ^{*}_kf\in C^r(\Omega )$
. Let
For an
![]() $h\in C^\infty _{tlc}(\Omega )$
and fixed
$h\in C^\infty _{tlc}(\Omega )$
and fixed
![]() $p\in \Omega $
, the function
$p\in \Omega $
, the function
![]() $f_h(t):=h\circ \varphi _t(p):\mathbb {R}^d\rightarrow \mathbb {R}$
is called p-equivariant.
$f_h(t):=h\circ \varphi _t(p):\mathbb {R}^d\rightarrow \mathbb {R}$
is called p-equivariant.
For a function f on
![]() $\Omega $
, define the transversal Hölder seminorm
$\Omega $
, define the transversal Hölder seminorm
 $$ \begin{align} |f|^{\perp}_{\alpha} = \sup_{x\in \Omega_\gamma} \sup_{x\neq y\in C^{\perp}_0(x)}\frac{| f(x)-f(y)|}{d(x,y)^\alpha}, \end{align} $$
$$ \begin{align} |f|^{\perp}_{\alpha} = \sup_{x\in \Omega_\gamma} \sup_{x\neq y\in C^{\perp}_0(x)}\frac{| f(x)-f(y)|}{d(x,y)^\alpha}, \end{align} $$
and let
![]() $H_{\alpha }^{\perp }(\Omega )$
be the Banach space of transversally
$H_{\alpha }^{\perp }(\Omega )$
be the Banach space of transversally
![]() $\alpha $
-Hölder functions with norm
$\alpha $
-Hölder functions with norm
Note that for any
![]() $0<\beta <\alpha $
, there is a compact inclusion
$0<\beta <\alpha $
, there is a compact inclusion
![]() $H^{\perp }_{\alpha } \subset H^{\perp }_\beta $
.
$H^{\perp }_{\alpha } \subset H^{\perp }_\beta $
.
Remark 2.2. Since the local transversals
![]() $C^{\perp }_k$
are totally disconnected sets, the spaces
$C^{\perp }_k$
are totally disconnected sets, the spaces
![]() $H_{\alpha }^{\perp }(\Omega )$
are non-trivial for every real
$H_{\alpha }^{\perp }(\Omega )$
are non-trivial for every real
![]() $\alpha>0$
. This is a significant difference from stable sets which are smooth, and
$\alpha>0$
. This is a significant difference from stable sets which are smooth, and
![]() $\alpha $
here controls the analogous quantity for smoothness in a totally disconnected direction of
$\alpha $
here controls the analogous quantity for smoothness in a totally disconnected direction of
![]() $\Omega $
.
$\Omega $
.
Let
![]() $C^r(\Omega )$
denote the set of functions f on
$C^r(\Omega )$
denote the set of functions f on
![]() $\Omega $
such that
$\Omega $
such that
![]() $\partial _{v_{i_1}}\cdots \partial _{v_{i_r}} f$
is continuous for any choice of r vectors
$\partial _{v_{i_1}}\cdots \partial _{v_{i_r}} f$
is continuous for any choice of r vectors
![]() $v_{i_j}$
in an orthonormal basis
$v_{i_j}$
in an orthonormal basis
![]() $\{v_1,\ldots v_d\}$
of
$\{v_1,\ldots v_d\}$
of
![]() $\mathbb {R}^d$
. Finally, define for
$\mathbb {R}^d$
. Finally, define for
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>0$
,
$\alpha>0$
,
 $$ \begin{align} C^r_{\alpha}(\Omega) = \bigg\{f\in C^r(\Omega)\cap H^{\perp}_{\alpha}(\Omega): \sum_{0\leq p \leq r}\sum_{|i|=p} \|\partial^if\|_{C^0}+|\partial^i f|^{\perp}_{\alpha} < \infty \bigg\} \end{align} $$
$$ \begin{align} C^r_{\alpha}(\Omega) = \bigg\{f\in C^r(\Omega)\cap H^{\perp}_{\alpha}(\Omega): \sum_{0\leq p \leq r}\sum_{|i|=p} \|\partial^if\|_{C^0}+|\partial^i f|^{\perp}_{\alpha} < \infty \bigg\} \end{align} $$
to be the space of functions which not only are
![]() $C^r$
smooth in the leaf direction but also whose derivatives up to order r are transversally
$C^r$
smooth in the leaf direction but also whose derivatives up to order r are transversally
![]() $\alpha $
-Hölder. Here the traditional multiindex notation
$\alpha $
-Hölder. Here the traditional multiindex notation
![]() $i = (i_1,\ldots , i_d)$
has been used, with
$i = (i_1,\ldots , i_d)$
has been used, with
![]() $|i|=i_1+\cdots + i_d$
. This is a Banach space under the norm
$|i|=i_1+\cdots + i_d$
. This is a Banach space under the norm
 $$ \begin{align} \|f\|_{r,\alpha}:= \sum_{0\leq p \leq r}\sum_{|i|=p} \|\partial^if\|_{C^0}+|\partial^i f|^{\perp}_{\alpha}. \end{align} $$
$$ \begin{align} \|f\|_{r,\alpha}:= \sum_{0\leq p \leq r}\sum_{|i|=p} \|\partial^if\|_{C^0}+|\partial^i f|^{\perp}_{\alpha}. \end{align} $$
Given a function
![]() $f\in L^1(\Omega )$
and
$f\in L^1(\Omega )$
and
![]() $k\in \mathbb {N}_0:= \mathbb {N}\cup \{0\}$
, set
$k\in \mathbb {N}_0:= \mathbb {N}\cup \{0\}$
, set
 $$ \begin{align} \Pi_k f(x):= \hat\nu_{k,x}^{-1}\int_{C_k^{\perp}(x)} f(z)\, d\nu_{k,x},\quad \Delta_kf := f-\Pi_k f,\quad\mbox{and}\quad\delta_kf := \Pi_kf-\Pi_{k-1}f. \end{align} $$
$$ \begin{align} \Pi_k f(x):= \hat\nu_{k,x}^{-1}\int_{C_k^{\perp}(x)} f(z)\, d\nu_{k,x},\quad \Delta_kf := f-\Pi_k f,\quad\mbox{and}\quad\delta_kf := \Pi_kf-\Pi_{k-1}f. \end{align} $$
These functions will be crucial for most results of this paper, so let me take some time to discuss how one can think of them. Any
![]() $f\in L^1_\mu (\Omega )$
is a function of infinitely many variables, since this is how the solenoid is defined. The function
$f\in L^1_\mu (\Omega )$
is a function of infinitely many variables, since this is how the solenoid is defined. The function
![]() $\Pi _k f$
is obtained by integrating along local transversals and consequently
$\Pi _k f$
is obtained by integrating along local transversals and consequently
![]() $\Pi _kf$
is transversally locally constant. This means that
$\Pi _kf$
is transversally locally constant. This means that
![]() $\Pi _k f$
only depends on finitely many coordinates, that is, there is a function
$\Pi _k f$
only depends on finitely many coordinates, that is, there is a function
![]() $g_k\in L^1(\Gamma )$
such that
$g_k\in L^1(\Gamma )$
such that
![]() $\Pi _k f = \pi ^{*}_k g_k$
. Thus,
$\Pi _k f = \pi ^{*}_k g_k$
. Thus,
![]() $\Pi _kf$
can be thought of as the best approximation to f if we can only consider the first k coordinates. We will see below that
$\Pi _kf$
can be thought of as the best approximation to f if we can only consider the first k coordinates. We will see below that
![]() $\Pi _kf\rightarrow f$
in a satisfying sense as
$\Pi _kf\rightarrow f$
in a satisfying sense as
![]() $k\rightarrow \infty $
.
$k\rightarrow \infty $
.
If
![]() $\Pi _k f$
is an approximation to f using the first k coordinates, then
$\Pi _k f$
is an approximation to f using the first k coordinates, then
![]() $\Delta _k f$
is the error in this approximation. If
$\Delta _k f$
is the error in this approximation. If
![]() $\Pi _kf\rightarrow f$
in some sense, then one should expect that
$\Pi _kf\rightarrow f$
in some sense, then one should expect that
![]() $\Delta _kf\rightarrow 0$
in the same sense (this will come up later). Finally, if
$\Delta _kf\rightarrow 0$
in the same sense (this will come up later). Finally, if
![]() $\Pi _kf$
is an approximation to f using the first k coordinates, then
$\Pi _kf$
is an approximation to f using the first k coordinates, then
![]() $f_k:=\delta _k f$
is the best approximation to f using only the
$f_k:=\delta _k f$
is the best approximation to f using only the
![]() $k\mathrm {th}$
coordinate. So after setting
$k\mathrm {th}$
coordinate. So after setting
![]() $\Pi _{-1}f =0$
, the approximation
$\Pi _{-1}f =0$
, the approximation
![]() $\Pi _k f$
can be written as the finite sum
$\Pi _k f$
can be written as the finite sum
 $$ \begin{align*} \Pi_k f = \sum_{i=0}^k \delta_k f = \sum_{i=0}^k f_k \end{align*} $$
$$ \begin{align*} \Pi_k f = \sum_{i=0}^k \delta_k f = \sum_{i=0}^k f_k \end{align*} $$
and so if
![]() $\Pi _kf\rightarrow f$
, then f can be written as a sum
$\Pi _kf\rightarrow f$
, then f can be written as a sum
![]() $f = \sum f_k$
in a canonical way. These of course are rough descriptions of how one can think of these functions but since they will appear regularly in this paper, one should have a good way to think of them.
$f = \sum f_k$
in a canonical way. These of course are rough descriptions of how one can think of these functions but since they will appear regularly in this paper, one should have a good way to think of them.
A more precise description of what is happening involves conditional expectation. For
![]() $k\in \mathbb {N}_0$
, let
$k\in \mathbb {N}_0$
, let
![]() $\mathcal {A}_k$
be the
$\mathcal {A}_k$
be the
![]() $\sigma $
-algebra generated by the preimages
$\sigma $
-algebra generated by the preimages
![]() $\pi ^{-1}_k(A)$
of Borel sets
$\pi ^{-1}_k(A)$
of Borel sets
![]() $A\subset \Gamma _k$
. This is an increasing sequence of sub-
$A\subset \Gamma _k$
. This is an increasing sequence of sub-
![]() $\sigma $
-algebras of the Borel
$\sigma $
-algebras of the Borel
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\Omega $
. The conditional expectation
$\Omega $
. The conditional expectation
![]() $E(\cdot |\mathcal {A}_k):L^1(\Omega ,\mathcal {A},\mu )\rightarrow L^1(\Omega ,\mathcal {A}_k,\mu )$
map coincides with
$E(\cdot |\mathcal {A}_k):L^1(\Omega ,\mathcal {A},\mu )\rightarrow L^1(\Omega ,\mathcal {A}_k,\mu )$
map coincides with
![]() $\Pi _k$
, that is, for any
$\Pi _k$
, that is, for any
![]() $f\in L^1(\Omega ,\mu )$
,
$f\in L^1(\Omega ,\mu )$
,
![]() $E(f|\mathcal {A}_k) = \Pi _kf$
, and
$E(f|\mathcal {A}_k) = \Pi _kf$
, and
![]() $\nu _{k,x}$
is the conditional measure of this conditional expectation. By the increasing martingale theorem [Reference Einsiedler and WardEW11, Theorem 5.5],
$\nu _{k,x}$
is the conditional measure of this conditional expectation. By the increasing martingale theorem [Reference Einsiedler and WardEW11, Theorem 5.5],
![]() $\Pi _kf\rightarrow f$
almost everywhere and in
$\Pi _kf\rightarrow f$
almost everywhere and in
![]() $L^1$
.
$L^1$
.
Using the notation
![]() $f_k = \delta _k f$
from above, for
$f_k = \delta _k f$
from above, for
![]() $r,\alpha \geq 0$
, let
$r,\alpha \geq 0$
, let

Let me make two comments which motivate the definition of these function spaces. The first one comes from the algebraic setting: if S is the inverse limit of locally expanding affine linear maps of
![]() $\mathbb {T}^d$
, then
$\mathbb {T}^d$
, then
![]() $L^2_\mu $
is spanned by a Fourier basis, and so one needs to quantify the decay rates of the Fourier coefficients to capture degrees of regularity. The generalization of this idea leads to the space
$L^2_\mu $
is spanned by a Fourier basis, and so one needs to quantify the decay rates of the Fourier coefficients to capture degrees of regularity. The generalization of this idea leads to the space
![]() $\mathcal {S}^r_{\alpha }$
as defined above. The second reason is that the representation of a function as a sum of pullbacks of distinct functions on approximants is canonical: if
$\mathcal {S}^r_{\alpha }$
as defined above. The second reason is that the representation of a function as a sum of pullbacks of distinct functions on approximants is canonical: if
![]() $f = \pi ^{*}_0f^{(0)}$
, then f is transversally locally constant, so
$f = \pi ^{*}_0f^{(0)}$
, then f is transversally locally constant, so
![]() $\delta _kf = 0$
for all
$\delta _kf = 0$
for all
![]() $k>0$
, and so the f is uniquely represented as a sum of finitely many terms.
$k>0$
, and so the f is uniquely represented as a sum of finitely many terms.
Proposition 2.3. For the spaces
![]() $\mathcal {S}^r_{\alpha }(\Omega )$
and
$\mathcal {S}^r_{\alpha }(\Omega )$
and
![]() $C^r_{\alpha }(\Omega )$
defined above with
$C^r_{\alpha }(\Omega )$
defined above with
![]() $r\in \mathbb {N},\alpha>0$
:
$r\in \mathbb {N},\alpha>0$
:
-
(i) for any
 $v\in \{v_1,\ldots , v_d\}$
, if
$v\in \{v_1,\ldots , v_d\}$
, if
 $f\in \mathcal {S}^r_{\alpha }(\Omega )$
, then
$f\in \mathcal {S}^r_{\alpha }(\Omega )$
, then
 $\partial _{v}f\in \mathcal {S}^{r-1}_{\alpha +1}(\Omega )$
,
$\partial _{v}f\in \mathcal {S}^{r-1}_{\alpha +1}(\Omega )$
, -
(ii) for any
 $\varepsilon \in (0,\alpha )$
,
$\varepsilon \in (0,\alpha )$
,
 $\mathcal {S}^r_{\alpha }(\Omega )\subset C^r_{\alpha }(\Omega )$
densely with respect to the norm of
$\mathcal {S}^r_{\alpha }(\Omega )\subset C^r_{\alpha }(\Omega )$
densely with respect to the norm of
 $C^r_{\alpha -\varepsilon }(\Omega )$
.
$C^r_{\alpha -\varepsilon }(\Omega )$
.
Remark 2.4. I would like to remark on the surprising feature in item (i): taking leafwise derivatives increases regularity in the transverse direction. Since this is the Hölder regularity, this depends on the metric used. The form adopted here is the one which corresponds to the natural choice of transversal metric in equation (3), as well as using the same number
![]() $\unicode{x3bb} _0$
in defining the spaces
$\unicode{x3bb} _0$
in defining the spaces
![]() $\mathcal {S}^r_{\alpha }(\Omega )$
.
$\mathcal {S}^r_{\alpha }(\Omega )$
.
Proof of Proposition 2.3
For item (i), if
![]() $f\in \mathcal {S}^r_{\alpha }$
, then using equations (4) and (6),
$f\in \mathcal {S}^r_{\alpha }$
, then using equations (4) and (6),
and
So
![]() $\partial _v f \in \mathcal {S}_{\alpha +1}^{r-1}(\Omega )$
.
$\partial _v f \in \mathcal {S}_{\alpha +1}^{r-1}(\Omega )$
.
For item (ii), for
![]() $f\in C^r_{\alpha }$
, consider the approximations
$f\in C^r_{\alpha }$
, consider the approximations
![]() $\Pi _k f$
. For every k, these approximations are all in
$\Pi _k f$
. For every k, these approximations are all in
![]() $\mathcal {S}^r_{\alpha }$
for any
$\mathcal {S}^r_{\alpha }$
for any
![]() $\alpha>0$
since they are transversally local functions. What needs to be proved is that for any multiindex i with
$\alpha>0$
since they are transversally local functions. What needs to be proved is that for any multiindex i with
![]() $|i|\leq r$
,
$|i|\leq r$
,
as
![]() $k\rightarrow \infty $
.
$k\rightarrow \infty $
.
Let i be one such multiindex. Then

and so
![]() $\|\partial ^i\Pi _kf - \partial ^if\|_{C^0}\rightarrow 0$
. Here it was used that not only f but its derivatives are transversally
$\|\partial ^i\Pi _kf - \partial ^if\|_{C^0}\rightarrow 0$
. Here it was used that not only f but its derivatives are transversally
![]() $\alpha $
-Hölder.
$\alpha $
-Hölder.
Let
![]() $x\in \Omega $
and suppose that
$x\in \Omega $
and suppose that
![]() $a,b\in C^{\perp }_\ell (x)$
. Then if
$a,b\in C^{\perp }_\ell (x)$
. Then if
![]() $\ell \leq k$
,
$\ell \leq k$
,

where equation (12) was used in simplifying the numerator. If
![]() $\ell>k$
,
$\ell>k$
,

And so
![]() $|\partial ^i\Pi _kf - \partial ^if|^{\perp }_{\alpha -\varepsilon }\rightarrow 0$
, so the proof is concluded.
$|\partial ^i\Pi _kf - \partial ^if|^{\perp }_{\alpha -\varepsilon }\rightarrow 0$
, so the proof is concluded.
3. Transversal Hölder cohomology for Wieler solenoids
Wieler solenoids, being defined as an inverse limit of surjective and locally expaning maps have the advantage that their (Čech) cohomology can be explicitly computed. At the most basic level, this can be done with coefficients in
![]() $\mathbb {Z}$
through
$\mathbb {Z}$
through
By the universal coefficient theorem and universality of inverse limits, the cohomology with real coefficients is
Likewise, since there is a free
![]() $\mathbb {R}^d$
action on
$\mathbb {R}^d$
action on
![]() $\Omega $
, there is an associated Lie-algebra cohomology defined as follows. Let
$\Omega $
, there is an associated Lie-algebra cohomology defined as follows. Let
![]() $X_1,\ldots , X_d$
be an orthonormal frame of
$X_1,\ldots , X_d$
be an orthonormal frame of
![]() $\mathbb {R}^d$
. Define the operators
$\mathbb {R}^d$
. Define the operators
![]() $\partial _i$
using
$\partial _i$
using
![]() $X_i$
as in equation (6). Let
$X_i$
as in equation (6). Let
![]() $C^\infty (\Omega ;\Lambda \mathbb {R}^{d*})$
be the space of leafwise smooth sections of
$C^\infty (\Omega ;\Lambda \mathbb {R}^{d*})$
be the space of leafwise smooth sections of
![]() $\Omega $
to
$\Omega $
to
![]() $\Lambda \mathbb {R}^{d*}$
, the graded exterior algebra of
$\Lambda \mathbb {R}^{d*}$
, the graded exterior algebra of
![]() $\mathbb {R}^{d*}$
. In other words,
$\mathbb {R}^{d*}$
. In other words,
![]() $C^\infty (\Omega ;\Lambda \mathbb {R}^{d*})$
is the space of functions
$C^\infty (\Omega ;\Lambda \mathbb {R}^{d*})$
is the space of functions
![]() $f:\Omega \rightarrow \Lambda \mathbb {R}^{d*}$
such that
$f:\Omega \rightarrow \Lambda \mathbb {R}^{d*}$
such that
![]() $\partial _{i_1}\cdots \partial _{i_k}f\in C^\infty (\Omega ;\Lambda \mathbb {R}^{d*})$
for any finite collection of indices
$\partial _{i_1}\cdots \partial _{i_k}f\in C^\infty (\Omega ;\Lambda \mathbb {R}^{d*})$
for any finite collection of indices
![]() $i_1,\ldots , i_k$
.
$i_1,\ldots , i_k$
.
Let
![]() $d:C^\infty (\Omega ;\Lambda ^k\mathbb {R}^{d*})\rightarrow C^\infty (\Omega ;\Lambda ^{k+1}\mathbb {R}^{d*}) $
be the exterior differential operator defined as follows. Let
$d:C^\infty (\Omega ;\Lambda ^k\mathbb {R}^{d*})\rightarrow C^\infty (\Omega ;\Lambda ^{k+1}\mathbb {R}^{d*}) $
be the exterior differential operator defined as follows. Let
![]() $\{dx_1,\ldots , dx_d\}$
denote the dual frame to
$\{dx_1,\ldots , dx_d\}$
denote the dual frame to
![]() $\{X_1,\ldots , X_d\}$
. Then
$\{X_1,\ldots , X_d\}$
. Then
 $$ \begin{align*}d(f dx_{i_1}\wedge\cdots \wedge dx_{i_k}) = \sum_{i=1}^d \partial_if dx_i\wedge dx_{i_1}\wedge \cdots \wedge dx_{i_k}.\end{align*} $$
$$ \begin{align*}d(f dx_{i_1}\wedge\cdots \wedge dx_{i_k}) = \sum_{i=1}^d \partial_if dx_i\wedge dx_{i_1}\wedge \cdots \wedge dx_{i_k}.\end{align*} $$
It is immediate to verify that this operator satisfies
![]() $d^2=0$
. Moreover, there is natural subcomplex
$d^2=0$
. Moreover, there is natural subcomplex
![]() $C^\infty _{tlc}(\Omega ;\Lambda ^k\mathbb {R}^{d*})$
of sections with tlc coefficients.
$C^\infty _{tlc}(\Omega ;\Lambda ^k\mathbb {R}^{d*})$
of sections with tlc coefficients.
Definition 3.1. The Lie-algebra cohomology
![]() $H^{*}(\Omega )$
of
$H^{*}(\Omega )$
of
![]() $\Omega $
is the cohomology of the differential complex
$\Omega $
is the cohomology of the differential complex
![]() $(C^\infty (\Omega ;\Lambda \mathbb {R}^{d*}),d)$
. That is,
$(C^\infty (\Omega ;\Lambda \mathbb {R}^{d*}),d)$
. That is,
 $$ \begin{align*} H^{\bullet}(\Omega):= \frac{\ker \{d:C^\infty(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\rightarrow C^\infty(\Omega;\Lambda^{\bullet+1}\mathbb{R}^{d*})\}}{\mathrm{Im}\, \{d:C^\infty(\Omega;\Lambda^{\bullet-1}\mathbb{R}^{d*})\rightarrow C^\infty(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\}}. \end{align*} $$
$$ \begin{align*} H^{\bullet}(\Omega):= \frac{\ker \{d:C^\infty(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\rightarrow C^\infty(\Omega;\Lambda^{\bullet+1}\mathbb{R}^{d*})\}}{\mathrm{Im}\, \{d:C^\infty(\Omega;\Lambda^{\bullet-1}\mathbb{R}^{d*})\rightarrow C^\infty(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\}}. \end{align*} $$
The transversally locally constant (tlc) Lie-algebra cohomology is the cohomology of the subcomplex of tlc functions:
 $$ \begin{align*} H^{\bullet}_{tlc}(\Omega):= \frac{\ker \{d:C^\infty_{tlc}(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\rightarrow C^\infty_{tlc}(\Omega;\Lambda^{\bullet+1}\mathbb{R}^{d*})\}}{\mathrm{Im}\, \{d:C^\infty_{tlc}(\Omega;\Lambda^{\bullet-1}\mathbb{R}^{d*})\rightarrow C^\infty_{tlc}(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\}}. \end{align*} $$
$$ \begin{align*} H^{\bullet}_{tlc}(\Omega):= \frac{\ker \{d:C^\infty_{tlc}(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\rightarrow C^\infty_{tlc}(\Omega;\Lambda^{\bullet+1}\mathbb{R}^{d*})\}}{\mathrm{Im}\, \{d:C^\infty_{tlc}(\Omega;\Lambda^{\bullet-1}\mathbb{R}^{d*})\rightarrow C^\infty_{tlc}(\Omega;\Lambda^{\bullet}\mathbb{R}^{d*})\}}. \end{align*} $$
Finally, there is one more type of cohomology which is relevant here: since for
![]() $p\in \Omega $
a form
$p\in \Omega $
a form
![]() $\eta \in C^\infty (\Omega ;\Lambda ^{*}\mathbb {R}^{d*})$
defines a p-equivariant form
$\eta \in C^\infty (\Omega ;\Lambda ^{*}\mathbb {R}^{d*})$
defines a p-equivariant form
![]() $\omega _\eta (t) := \varphi ^{*}_t\eta :\mathbb {R}^d\rightarrow \Lambda ^{*}\mathbb {R}^{d*}$
, the p-equivariant cohomology
$\omega _\eta (t) := \varphi ^{*}_t\eta :\mathbb {R}^d\rightarrow \Lambda ^{*}\mathbb {R}^{d*}$
, the p-equivariant cohomology
![]() $H^{*}_p(\Omega ;\mathbb {R})$
is defined as the cohomology of this subcomplex of the de Rham complex of
$H^{*}_p(\Omega ;\mathbb {R})$
is defined as the cohomology of this subcomplex of the de Rham complex of
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
Kellendonk and Putnam [Reference Kellendonk and PutnamKP06] proved that the p-equivariant cohomology is isomorphic to the tlc Lie-algebra cohomology, which in turn is isomorphic to the Čech cohomology in equation (13) with coefficients in
![]() $\mathbb {R}$
. In general, it is not true that
$\mathbb {R}$
. In general, it is not true that
![]() $H^{\bullet }_{tlc}(\Omega )$
is isomorphic to
$H^{\bullet }_{tlc}(\Omega )$
is isomorphic to
![]() $H^{\bullet }(\Omega )$
. These two cohomologies capture two extremes of regularity in the transverse direction: functions in
$H^{\bullet }(\Omega )$
. These two cohomologies capture two extremes of regularity in the transverse direction: functions in
![]() $C^\infty $
satisfy
$C^\infty $
satisfy
![]() $|f|^{\perp }_0<\infty $
, whereas
$|f|^{\perp }_0<\infty $
, whereas
![]() $g\in C^\infty _{tlc}$
has
$g\in C^\infty _{tlc}$
has
![]() $|g|_{\alpha }^{\perp }<\infty $
for all
$|g|_{\alpha }^{\perp }<\infty $
for all
![]() $\alpha \geq 0$
. Thus, it is natural to ask how much regularity is needed in the transverse direction to recover the real Čech cohomology. This is the transversally Hölder cohomology.
$\alpha \geq 0$
. Thus, it is natural to ask how much regularity is needed in the transverse direction to recover the real Čech cohomology. This is the transversally Hölder cohomology.
The rest of the section is devoted to proving that instead of looking at the cohomology of
![]() $C^\infty _{tlc}$
sections, one could consider the cohomology of sections with coefficients in
$C^\infty _{tlc}$
sections, one could consider the cohomology of sections with coefficients in
![]() $\mathcal {S}^r_{\alpha }(\Omega )$
or
$\mathcal {S}^r_{\alpha }(\Omega )$
or
![]() $C^r_{\alpha }$
. To do this, a name for this type of cohomology is needed.
$C^r_{\alpha }$
. To do this, a name for this type of cohomology is needed.
Definition 3.2. The space
![]() $\Psi ^m_{r,\alpha }$
is the space of m-forms
$\Psi ^m_{r,\alpha }$
is the space of m-forms
![]() $\eta :\Omega \rightarrow \Lambda ^m\mathbb {R}^{d*}$
with coefficients in
$\eta :\Omega \rightarrow \Lambda ^m\mathbb {R}^{d*}$
with coefficients in
![]() $\mathcal {S}^{r}_{\alpha }$
. That is, an element
$\mathcal {S}^{r}_{\alpha }$
. That is, an element
![]() $\Psi ^m_{r,\alpha }$
can be written as
$\Psi ^m_{r,\alpha }$
can be written as
where each
![]() $dx_I$
is an m-form of the form
$dx_I$
is an m-form of the form
![]() $dx_{i_1}\wedge \cdots \wedge dx_{i_m}$
, and
$dx_{i_1}\wedge \cdots \wedge dx_{i_m}$
, and
![]() $\eta _I\in \mathcal {S}^{r}_{\alpha }$
for all
$\eta _I\in \mathcal {S}^{r}_{\alpha }$
for all
![]() $I\in I_m$
. Let
$I\in I_m$
. Let
and define the
![]() $\mathcal {S}^{r}_{\alpha }$
-cohomology of
$\mathcal {S}^{r}_{\alpha }$
-cohomology of
![]() $\Omega $
as
$\Omega $
as
which is the Lie algebra cohomology with coefficients in
![]() $\Psi _{r,\alpha }^{*}$
.
$\Psi _{r,\alpha }^{*}$
.
Theorem 3.3. Fix
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>1$
, and let
$\alpha>1$
, and let
![]() $\eta \in \mathcal {Z}^m_{r,\alpha }$
. Then there exists
$\eta \in \mathcal {Z}^m_{r,\alpha }$
. Then there exists
![]() $\eta '\in C^\infty _{tlc}(\Omega ;\Lambda ^m\mathbb {R}^{d*})$
and
$\eta '\in C^\infty _{tlc}(\Omega ;\Lambda ^m\mathbb {R}^{d*})$
and
![]() $\omega \in \Psi ^{m-1}_{r+1,\alpha -1} $
such that
$\omega \in \Psi ^{m-1}_{r+1,\alpha -1} $
such that
![]() $\eta -\eta ' = d\omega $
. That is, for
$\eta -\eta ' = d\omega $
. That is, for
![]() $r\geq 1$
and
$r\geq 1$
and
![]() $\alpha>1$
,
$\alpha>1$
,
The rest of this section is devoted to the proof of this theorem. First, we start by reviewing de Rham cohomology for branched manifolds, then de Rham regularization for branched manifolds, and finally we put all of this together in the inverse limit structure.
Let
![]() $H^{*}_{r,tlc}(\Omega )$
be the Lie-algebra cohomology with
$H^{*}_{r,tlc}(\Omega )$
be the Lie-algebra cohomology with
![]() $C^r_{tlc}$
coefficients. That is, two forms
$C^r_{tlc}$
coefficients. That is, two forms
![]() $\eta _1,\eta _2$
are in the same cohomology class if there exists an
$\eta _1,\eta _2$
are in the same cohomology class if there exists an
![]() $\omega \in C^r_{tlc}$
such that
$\omega \in C^r_{tlc}$
such that
![]() $\eta _1-\eta _2 = d\omega $
.
$\eta _1-\eta _2 = d\omega $
.
Proposition 3.4. For
![]() $r\in \mathbb {N}$
,
$r\in \mathbb {N}$
,
![]() $H^{*}_{r,tlc}(\Omega )\cong H^{*}_{tlc}(\Omega )$
.
$H^{*}_{r,tlc}(\Omega )\cong H^{*}_{tlc}(\Omega )$
.
Proof. The goal is to show that for any closed
![]() $\eta \in C^r_{tlc}(\Omega ;\Lambda ^{*}\mathbb {R}^{d*})$
, there is an
$\eta \in C^r_{tlc}(\Omega ;\Lambda ^{*}\mathbb {R}^{d*})$
, there is an
![]() $\eta '\in C^\infty _{tlc}(\Omega ;\Lambda ^{*}\mathbb {R}^{d*}) $
and
$\eta '\in C^\infty _{tlc}(\Omega ;\Lambda ^{*}\mathbb {R}^{d*}) $
and
![]() $\omega \in C^{r}_{tlc}(\Omega ;\Lambda ^{*}\mathbb {R}^{d*})$
such that
$\omega \in C^{r}_{tlc}(\Omega ;\Lambda ^{*}\mathbb {R}^{d*})$
such that
![]() $\eta -\eta ' = d\omega $
. This will be done through the use of de Rham regularization [Reference de RhamdR84, §III.15] applied to p-equivariant cohomology, since it is isomorphic to Lie-algebra cohomology.
$\eta -\eta ' = d\omega $
. This will be done through the use of de Rham regularization [Reference de RhamdR84, §III.15] applied to p-equivariant cohomology, since it is isomorphic to Lie-algebra cohomology.
Let
![]() $p\in \Omega $
and let
$p\in \Omega $
and let
![]() $\eta :\mathbb {R}^d\rightarrow \Lambda ^{*}\mathbb {R}^{d*}$
be a p-equivariant form with
$\eta :\mathbb {R}^d\rightarrow \Lambda ^{*}\mathbb {R}^{d*}$
be a p-equivariant form with
![]() $C^r$
coefficients. This means there is an
$C^r$
coefficients. This means there is an
![]() $R_\eta>1$
such that if the tiling around the point x in a ball of radius
$R_\eta>1$
such that if the tiling around the point x in a ball of radius
![]() $R_\eta $
is the same as the one around y in a ball of radius
$R_\eta $
is the same as the one around y in a ball of radius
![]() $R_\eta $
, then
$R_\eta $
, then
![]() $\eta (x) = \eta (y)$
. This follows from the fact that
$\eta (x) = \eta (y)$
. This follows from the fact that
![]() $\eta (t) = \bar {\eta }\circ \varphi _t(p)$
for a transversally locally constant form
$\eta (t) = \bar {\eta }\circ \varphi _t(p)$
for a transversally locally constant form
![]() $\bar {\eta }$
. As such, there is a k such that
$\bar {\eta }$
. As such, there is a k such that
![]() $\bar {\eta }$
is constant on
$\bar {\eta }$
is constant on
![]() $C_k^{\perp }(x)$
for any x, and so if
$C_k^{\perp }(x)$
for any x, and so if
![]() $x,y\in \mathbb {R}^d$
are such that
$x,y\in \mathbb {R}^d$
are such that
![]() $\varphi _y(p) \in C_k^{\perp }(\varphi _x(p))$
, then
$\varphi _y(p) \in C_k^{\perp }(\varphi _x(p))$
, then
![]() $\eta (x) = \eta (y)$
.
$\eta (x) = \eta (y)$
.
Pick
![]() $\varepsilon \in (0,1/2)$
and let
$\varepsilon \in (0,1/2)$
and let
![]() $\mathcal {U} = \{U_i\}_{i\in \mathbb {N}}$
be a cover of
$\mathcal {U} = \{U_i\}_{i\in \mathbb {N}}$
be a cover of
![]() $\mathbb {R}^d$
such that:
$\mathbb {R}^d$
such that:
-
(i)
 $\mathcal {U}$
is locally finite;
$\mathcal {U}$
is locally finite; -
(ii)
 $U_i$
is an Euclidean ball of radius
$U_i$
is an Euclidean ball of radius
 $1+\varepsilon $
for all i;
$1+\varepsilon $
for all i; -
(iii)
 $\mathcal {U}$
is p-equivariant with radius
$\mathcal {U}$
is p-equivariant with radius
 $6R_\eta $
, that is, if
$6R_\eta $
, that is, if
 $U_i$
is centered at
$U_i$
is centered at
 $x_i$
and y has the same pattern as
$x_i$
and y has the same pattern as
 $x_i$
does inside a ball of radius
$x_i$
does inside a ball of radius
 $6R_\eta $
centered at y, then y is the center of some
$6R_\eta $
centered at y, then y is the center of some
 $U_j\in \mathcal {U}$
.
$U_j\in \mathcal {U}$
.
This type of cover is called a p-equivariant cover adapted to
![]() $\eta $
. A way to construct this type of cover is to cover
$\eta $
. A way to construct this type of cover is to cover
![]() $\Gamma _k$
with finitely many balls of the appropriate size so that when they lift to
$\Gamma _k$
with finitely many balls of the appropriate size so that when they lift to
![]() $\Omega $
, the intersection of leaves with these lifts are balls of size
$\Omega $
, the intersection of leaves with these lifts are balls of size
![]() $1+\varepsilon $
.
$1+\varepsilon $
.
Now, de Rham regularization can be invoked [Reference de RhamdR84, Theorem 12 in §III.15]: there exist operators R and A such that:
-
(i)
 $R\eta - \eta = dA\eta + Ad\eta $
;
$R\eta - \eta = dA\eta + Ad\eta $
; -
(ii)
 $R\eta \in C^\infty (\mathbb {R}^d;\Lambda ^{*}\mathbb {R}^{d*})$
; and
$R\eta \in C^\infty (\mathbb {R}^d;\Lambda ^{*}\mathbb {R}^{d*})$
; and -
(iii) if
 $\eta \in C^r(\mathbb {R}^d;\Lambda ^{*}\mathbb {R}^{d*})$
, then
$\eta \in C^r(\mathbb {R}^d;\Lambda ^{*}\mathbb {R}^{d*})$
, then
 $A\eta \in C^r(\mathbb {R}^d;\Lambda ^{*}\mathbb {R}^{d*})$
.
$A\eta \in C^r(\mathbb {R}^d;\Lambda ^{*}\mathbb {R}^{d*})$
.
Thus, if
![]() $d\eta = 0$
, then
$d\eta = 0$
, then
![]() $dR\eta = 0$
, and they differ by the exact
$dR\eta = 0$
, and they differ by the exact
![]() $C^r$
from
$C^r$
from
![]() $dA\eta $
. It remains to show that
$dA\eta $
. It remains to show that
![]() $A\eta $
is p-equivariant, that is, has something to do with
$A\eta $
is p-equivariant, that is, has something to do with
![]() $\Omega $
.
$\Omega $
.
Since
![]() $\mathcal {U}$
is a p-equivariant cover adapted to
$\mathcal {U}$
is a p-equivariant cover adapted to
![]() $\eta $
, if
$\eta $
, if
![]() $x,y\in \mathbb {R}^d$
have neighborhoods of radius
$x,y\in \mathbb {R}^d$
have neighborhoods of radius
![]() $6R_\eta $
which are translation equivalent, then
$6R_\eta $
which are translation equivalent, then
![]() $\eta \circ \varphi _\tau (x)=\eta \circ \varphi _\tau (y)$
for all
$\eta \circ \varphi _\tau (x)=\eta \circ \varphi _\tau (y)$
for all
![]() $\tau $
such that
$\tau $
such that
![]() $\|\tau \|\leq 5R_\eta $
and the union of the sets
$\|\tau \|\leq 5R_\eta $
and the union of the sets
![]() $U_1^x,\ldots , U_k^x$
which contain x is a set which is translation equivalent to the union of the sets
$U_1^x,\ldots , U_k^x$
which contain x is a set which is translation equivalent to the union of the sets
![]() $U_1^y,\ldots U^y_k$
which contain y. As such, the regularization at x is the same as the one at y, that is,
$U_1^y,\ldots U^y_k$
which contain y. As such, the regularization at x is the same as the one at y, that is,
![]() $A\eta (x) = A\eta (y)$
, which means that
$A\eta (x) = A\eta (y)$
, which means that
![]() $A\eta $
is p-equivariant.
$A\eta $
is p-equivariant.
Let
![]() $\Gamma $
be a flat branched manifold of dimension d, where the set of branches is denoted by
$\Gamma $
be a flat branched manifold of dimension d, where the set of branches is denoted by
![]() $B\subset \Gamma $
. Denote by
$B\subset \Gamma $
. Denote by
![]() $I^k$
the k-skeleton of
$I^k$
the k-skeleton of
![]() $\Gamma $
. For each
$\Gamma $
. For each
![]() $x\in B_k:= B\cap (I^k\setminus I^{k-1})$
, there is a natural tangent space
$x\in B_k:= B\cap (I^k\setminus I^{k-1})$
, there is a natural tangent space
![]() $T_x\Gamma $
of dimension k and a corresponding cotangent space. Let
$T_x\Gamma $
of dimension k and a corresponding cotangent space. Let
![]() $\Delta _{\ell }^{k}$
be the set of smooth
$\Delta _{\ell }^{k}$
be the set of smooth
![]() $\ell $
-forms on
$\ell $
-forms on
![]() $B_k$
, on which there is the usual de Rham differential operator
$B_k$
, on which there is the usual de Rham differential operator
![]() $d_k: \Delta _{\ell }^{k}\rightarrow \Delta _{\ell +1}^{k}$
and which are included in
$d_k: \Delta _{\ell }^{k}\rightarrow \Delta _{\ell +1}^{k}$
and which are included in
![]() $\Gamma $
using maps
$\Gamma $
using maps
![]() $i_k:B_k \rightarrow \Gamma $
. To give the entire branched space a smooth structure, consider the space of smooth maps
$i_k:B_k \rightarrow \Gamma $
. To give the entire branched space a smooth structure, consider the space of smooth maps
with coboundary operators
![]() $d:\Delta _k(\Gamma )\rightarrow \Delta _{k+1}(\Gamma )$
satisfying
$d:\Delta _k(\Gamma )\rightarrow \Delta _{k+1}(\Gamma )$
satisfying
![]() $d_k\circ i_k^{*} = i_k^{*}\circ d$
for all
$d_k\circ i_k^{*} = i_k^{*}\circ d$
for all
![]() $k\geq 0$
, that is, the operators which are conjugated to
$k\geq 0$
, that is, the operators which are conjugated to
![]() $d_k$
by
$d_k$
by
![]() $i_k^{*}$
for all k:
$i_k^{*}$
for all k:

Another way to characterize
![]() $\Delta _m(\Gamma )$
is the set of m-forms
$\Delta _m(\Gamma )$
is the set of m-forms
![]() $\eta $
on
$\eta $
on
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\pi ^{*}_k\eta $
is a
$\pi ^{*}_k\eta $
is a
![]() $C^\infty $
m-form on
$C^\infty $
m-form on
![]() $\Omega $
.
$\Omega $
.
Definition 3.5. The de Rham cohomology
![]() $H_{dR}^{*}(\Gamma )$
of the flat branched manifold
$H_{dR}^{*}(\Gamma )$
of the flat branched manifold
![]() $\Gamma $
is the cohomology of the complex
$\Gamma $
is the cohomology of the complex
![]() $(\Delta _*(\Gamma ),d)$
of smooth forms satisfying equation (14).
$(\Delta _*(\Gamma ),d)$
of smooth forms satisfying equation (14).
Sadun [Reference SadunSad07] proved that
![]() $H_{dR}^{*}(\Gamma )$
is isomorphic to the real Čech cohomology of
$H_{dR}^{*}(\Gamma )$
is isomorphic to the real Čech cohomology of
![]() $\Gamma $
.
$\Gamma $
.
Lemma 3.6. For
![]() $\rho \in [1,\infty ]$
, let
$\rho \in [1,\infty ]$
, let
![]() $\|\cdot \|':H^{*}_{\rho ,tlc}(\Omega )\rightarrow \mathbb {R}$
be a norm. Then there exists a K depending on the norm and on
$\|\cdot \|':H^{*}_{\rho ,tlc}(\Omega )\rightarrow \mathbb {R}$
be a norm. Then there exists a K depending on the norm and on
![]() $\gamma $
such that
$\gamma $
such that
for any closed
![]() $\eta \in \Delta _*(\Gamma _k) $
which is
$\eta \in \Delta _*(\Gamma _k) $
which is
![]() $C^r$
,
$C^r$
,
![]() $k\geq 0$
, and
$k\geq 0$
, and
![]() $r\in [1,\rho ]$
.
$r\in [1,\rho ]$
.
Proof. Since
![]() $H^i_{tlc}(\Omega )$
is finite dimensional, by Proposition 3.4, it will suffice to prove it for some norm. Let
$H^i_{tlc}(\Omega )$
is finite dimensional, by Proposition 3.4, it will suffice to prove it for some norm. Let
![]() $\|\cdot \|$
be some norm on
$\|\cdot \|$
be some norm on
![]() $H_i(\Gamma _k;\mathbb {R})$
and denote by
$H_i(\Gamma _k;\mathbb {R})$
and denote by
![]() $\|\cdot \|$
the dual norm on
$\|\cdot \|$
the dual norm on
![]() $H^i(\Gamma _k;\mathbb {R})$
. That is, for a closed i-form
$H^i(\Gamma _k;\mathbb {R})$
. That is, for a closed i-form
![]() $\eta \in \Delta _i(\Gamma _k)$
,
$\eta \in \Delta _i(\Gamma _k)$
,
 $$ \begin{align*}\|[\eta]\| = \sup_{0\neq [c] \in H_i(\Gamma_k;\mathbb{R})} \bigg|\frac{[\eta]([c])}{\|[c]\|}\bigg| = \sup_{0\neq [c] \in H_i(\Gamma_k;\mathbb{R})} \|[c]\|^{-1}\bigg|\!\int_c\eta\bigg|.\end{align*} $$
$$ \begin{align*}\|[\eta]\| = \sup_{0\neq [c] \in H_i(\Gamma_k;\mathbb{R})} \bigg|\frac{[\eta]([c])}{\|[c]\|}\bigg| = \sup_{0\neq [c] \in H_i(\Gamma_k;\mathbb{R})} \|[c]\|^{-1}\bigg|\!\int_c\eta\bigg|.\end{align*} $$
The
![]() $i\mathrm {th}$
skeleton of
$i\mathrm {th}$
skeleton of
![]() $\Gamma _k$
is finitely generated and so there is a collection of representative cycles
$\Gamma _k$
is finitely generated and so there is a collection of representative cycles
![]() $c_1,\ldots , c_m$
of a basis of
$c_1,\ldots , c_m$
of a basis of
![]() $H_i(\Gamma _k;\mathbb {Z})$
. Thus, for an integral class
$H_i(\Gamma _k;\mathbb {Z})$
. Thus, for an integral class
![]() $[c] = \sum _{j=1}^m a_j(c) c_j\in H_i(\Gamma _k;\mathbb {Z})$
, the absolute value of
$[c] = \sum _{j=1}^m a_j(c) c_j\in H_i(\Gamma _k;\mathbb {Z})$
, the absolute value of
![]() $\int _c\eta $
can be bounded as
$\int _c\eta $
can be bounded as
 $$ \begin{align} \bigg|\!\int_c\eta\bigg|&= \bigg|\sum_{j=1}^m a_j(c) \int_{c_j}\eta\bigg|\leq \sum_{j=1}^m |a_j(c)| \bigg|\!\int_{c_j}\eta\bigg| \leq \|\eta\|_{C^r(\Gamma_k)}\sum_{j=1}^m |a_j(c)\bigg| \mathrm{Vol}_i(c_j)\nonumber \\ &\leq K' (\max_j\mathrm{Vol}_i(c_j)) \|[c]\|\|\eta\|_{C^r(\Gamma_k)} \leq K"\|[c]\|\|\eta\|_{C^r(\Gamma_k)}, \end{align} $$
$$ \begin{align} \bigg|\!\int_c\eta\bigg|&= \bigg|\sum_{j=1}^m a_j(c) \int_{c_j}\eta\bigg|\leq \sum_{j=1}^m |a_j(c)| \bigg|\!\int_{c_j}\eta\bigg| \leq \|\eta\|_{C^r(\Gamma_k)}\sum_{j=1}^m |a_j(c)\bigg| \mathrm{Vol}_i(c_j)\nonumber \\ &\leq K' (\max_j\mathrm{Vol}_i(c_j)) \|[c]\|\|\eta\|_{C^r(\Gamma_k)} \leq K"\|[c]\|\|\eta\|_{C^r(\Gamma_k)}, \end{align} $$
where
![]() $K'$
comes from the equivalence of the
$K'$
comes from the equivalence of the
![]() $L^1$
norm and
$L^1$
norm and
![]() $\|\cdot \|$
in
$\|\cdot \|$
in
![]() $H_i(\Gamma _k;\mathbb {R})$
, and
$H_i(\Gamma _k;\mathbb {R})$
, and
![]() $\mathrm {Vol}_i(c_j)$
is the i-dimensional volume of the cycle
$\mathrm {Vol}_i(c_j)$
is the i-dimensional volume of the cycle
![]() $c_j$
. Here, it was used that
$c_j$
. Here, it was used that
![]() $\int _{c_j}\eta $
can be bounded by the volume of the cycle times the
$\int _{c_j}\eta $
can be bounded by the volume of the cycle times the
![]() $C^1$
norm of
$C^1$
norm of
![]() $\eta $
. Thus, it follows that
$\eta $
. Thus, it follows that
 $$ \begin{align*} \|[\pi^{*}_k\eta]\| = \|[\eta]\| = \sup_{0\neq c \in H_i(\Gamma_k;\mathbb{R})} \|c\|^{-1}\bigg|\!\int_c\eta\bigg| \leq K \|\eta\|_{C^r(\Gamma_k)}\end{align*} $$
$$ \begin{align*} \|[\pi^{*}_k\eta]\| = \|[\eta]\| = \sup_{0\neq c \in H_i(\Gamma_k;\mathbb{R})} \|c\|^{-1}\bigg|\!\int_c\eta\bigg| \leq K \|\eta\|_{C^r(\Gamma_k)}\end{align*} $$
for any
![]() $r\geq 1$
.
$r\geq 1$
.
The following completes the proof of Theorem 3.3.
Proposition 3.7. If
![]() $r\in \mathbb {N},\alpha>1$
, then
$r\in \mathbb {N},\alpha>1$
, then
![]() $\mathcal {H}^{*}_{r,\alpha }(\Omega )\cong H^{*}_{tlc}(\Omega )$
.
$\mathcal {H}^{*}_{r,\alpha }(\Omega )\cong H^{*}_{tlc}(\Omega )$
.
Proof. Let
![]() $\eta :\Omega \rightarrow \Lambda ^{*}\mathbb {R}^{d*}$
be a closed form with coefficients in
$\eta :\Omega \rightarrow \Lambda ^{*}\mathbb {R}^{d*}$
be a closed form with coefficients in
![]() $\mathcal {S}^r_{\alpha }(\Omega )$
with
$\mathcal {S}^r_{\alpha }(\Omega )$
with
![]() $r\geq 1$
and
$r\geq 1$
and
![]() $\alpha>1$
. By Proposition 3.4, it suffices to show that there is a form
$\alpha>1$
. By Proposition 3.4, it suffices to show that there is a form
![]() $\eta '\in H^{*}_{r,tlc}(\Omega )$
such that
$\eta '\in H^{*}_{r,tlc}(\Omega )$
such that
![]() $\eta -\eta ' = d\omega $
for some
$\eta -\eta ' = d\omega $
for some
![]() $\omega $
with coefficients in
$\omega $
with coefficients in
![]() $\mathcal {S}^{r+1}_{\alpha -1}$
.
$\mathcal {S}^{r+1}_{\alpha -1}$
.
By the definition of
![]() $\mathcal {S}^r_{\alpha }(\Omega )$
for each
$\mathcal {S}^r_{\alpha }(\Omega )$
for each
![]() $k\geq 0$
, there exists
$k\geq 0$
, there exists
![]() $\eta _k\in \Delta _*(\Gamma _k)$
such that
$\eta _k\in \Delta _*(\Gamma _k)$
such that
![]() $\eta $
is canonically expressed as
$\eta $
is canonically expressed as
![]() $\eta = \sum \nolimits _{k\geq 0} \delta _k\eta _k= \sum _{k\geq 0} \pi ^{*}_k\eta _k$
(see §2.1), where there are infinitely many non-zero terms, as that would otherwise make
$\eta = \sum \nolimits _{k\geq 0} \delta _k\eta _k= \sum _{k\geq 0} \pi ^{*}_k\eta _k$
(see §2.1), where there are infinitely many non-zero terms, as that would otherwise make
![]() $\eta $
a tlc form. Note that this expression for
$\eta $
a tlc form. Note that this expression for
![]() $\eta $
has the property that
$\eta $
has the property that
![]() $\eta _k\neq \gamma ^{*} \eta '$
for some
$\eta _k\neq \gamma ^{*} \eta '$
for some
![]() $\eta '\in \Delta _*(\Gamma _{k-1})$
. Now define the sequence of forms
$\eta '\in \Delta _*(\Gamma _{k-1})$
. Now define the sequence of forms
 $$ \begin{align*}\eta^{(n)}:= \sum_{k=0}^n \pi^{*}_k\eta_k.\end{align*} $$
$$ \begin{align*}\eta^{(n)}:= \sum_{k=0}^n \pi^{*}_k\eta_k.\end{align*} $$
Each of these forms is a closed tlc form. Indeed,
 $$ \begin{align*} 0=d\eta = d\bigg(\sum_{k\geq 0} \pi^{*}_k\eta_k \bigg)= \sum_{k\geq 0} d\pi^{*}_k\eta_k = \sum_{k\geq 0} d\delta_k \eta = \sum_{k\geq 0} \delta_k d\eta, \end{align*} $$
$$ \begin{align*} 0=d\eta = d\bigg(\sum_{k\geq 0} \pi^{*}_k\eta_k \bigg)= \sum_{k\geq 0} d\pi^{*}_k\eta_k = \sum_{k\geq 0} d\delta_k \eta = \sum_{k\geq 0} \delta_k d\eta, \end{align*} $$
since
![]() $d\Pi _k\eta = \Pi _k d\eta $
by the preservation of the transverse measure. Thus,
$d\Pi _k\eta = \Pi _k d\eta $
by the preservation of the transverse measure. Thus,
![]() $d\delta _k\eta = \delta _kd\eta = \delta _k 0 = 0$
for all k. It follows that
$d\delta _k\eta = \delta _kd\eta = \delta _k 0 = 0$
for all k. It follows that
![]() $\eta ^{(n)}$
has a tlc cohomology class
$\eta ^{(n)}$
has a tlc cohomology class
![]() $[\eta ^{(n)}]\in H^{*}_{r,tlc}(\Omega )$
. Observe that
$[\eta ^{(n)}]\in H^{*}_{r,tlc}(\Omega )$
. Observe that
![]() $[\eta ^{(n)}]$
is a convergent sequence. Indeed, by Lemma 3.6, for
$[\eta ^{(n)}]$
is a convergent sequence. Indeed, by Lemma 3.6, for
![]() $n>m>0$
,
$n>m>0$
,

Thus,
![]() $[\eta ]$
should be assigned the cohomology class
$[\eta ]$
should be assigned the cohomology class
![]() $\lim _{n\rightarrow \infty }[\eta ^{(n)}] \in H^{*}_{r,tlc}(\Omega )$
and so the goal is to find a tlc representative of this class and show that
$\lim _{n\rightarrow \infty }[\eta ^{(n)}] \in H^{*}_{r,tlc}(\Omega )$
and so the goal is to find a tlc representative of this class and show that
![]() $\eta $
is cohomologous to it.
$\eta $
is cohomologous to it.
Recall the eventual range
where
![]() $\beta _i = \dim H^i(\Gamma ;\mathbb {R})$
. Any class
$\beta _i = \dim H^i(\Gamma ;\mathbb {R})$
. Any class
![]() $c\in \check H^i(\Omega ;\mathbb {R})$
is represented by a class in
$c\in \check H^i(\Omega ;\mathbb {R})$
is represented by a class in
![]() $ER_i(\Omega )\subset \check H^i(\Gamma _{\beta _i};\mathbb {R})$
. Since
$ER_i(\Omega )\subset \check H^i(\Gamma _{\beta _i};\mathbb {R})$
. Since
![]() $\check H^i(\Gamma ;\mathbb {R})$
is isomorphic to
$\check H^i(\Gamma ;\mathbb {R})$
is isomorphic to
![]() $H^i_{dR}(\Gamma )$
[Reference SadunSad07, Appendix A], any class
$H^i_{dR}(\Gamma )$
[Reference SadunSad07, Appendix A], any class
![]() $c\in H^i_{tlc}(\Omega )$
has a representative
$c\in H^i_{tlc}(\Omega )$
has a representative
![]() $ \pi _{\beta _i}^{*} \eta _c$
coming from the
$ \pi _{\beta _i}^{*} \eta _c$
coming from the
![]() $\beta _i^{\mathrm {th}}$
projection map.
$\beta _i^{\mathrm {th}}$
projection map.
Let
![]() $\pi ^{*}_{\beta _i}\eta ^{\prime }_k$
be the form cohomologous to
$\pi ^{*}_{\beta _i}\eta ^{\prime }_k$
be the form cohomologous to
![]() $\pi _k^{*}\eta _k$
and let
$\pi _k^{*}\eta _k$
and let
 $$ \begin{align*} \eta_{(n)} = \sum_{k=0}^n \pi^{*}_{\beta_i}\eta^{\prime}_k = \pi^{*}_{\beta_i}\bigg(\sum_{k=0}^n \eta^{\prime}_k\bigg). \end{align*} $$
$$ \begin{align*} \eta_{(n)} = \sum_{k=0}^n \pi^{*}_{\beta_i}\eta^{\prime}_k = \pi^{*}_{\beta_i}\bigg(\sum_{k=0}^n \eta^{\prime}_k\bigg). \end{align*} $$
Then
![]() $\eta _{(n)} - \eta ^{(n)} = d\omega _n$
for all n. In addition,
$\eta _{(n)} - \eta ^{(n)} = d\omega _n$
for all n. In addition,
 $$ \begin{align*} \eta_{(\infty)} := \lim_{n\rightarrow \infty}\sum_{k=0}^n \pi^{*}_{\beta_i}\eta^{\prime}_k = \pi^{*}_{\beta_i}\bigg(\lim_{n\rightarrow \infty}\sum_{k=0}^n \eta^{\prime}_k\bigg) \end{align*} $$
$$ \begin{align*} \eta_{(\infty)} := \lim_{n\rightarrow \infty}\sum_{k=0}^n \pi^{*}_{\beta_i}\eta^{\prime}_k = \pi^{*}_{\beta_i}\bigg(\lim_{n\rightarrow \infty}\sum_{k=0}^n \eta^{\prime}_k\bigg) \end{align*} $$
is a
![]() $C^r$
tlc function which is cohomologous to
$C^r$
tlc function which is cohomologous to
![]() $\eta $
.
$\eta $
.
3.1. Application: deviations of ergodic averages
The spectrum of
![]() $\Phi ^{*}:\check H^d(\Omega ;\mathbb {R})\rightarrow \check H^d(\Omega ;\mathbb {R})$
gives rates of convergence of ergodic integrals. This was first proved in [Reference SadunSad11] in the self-similar case and later in [Reference Schmieding and TreviñoST18] in the self-affine case. The class of functions used in those results were
$\Phi ^{*}:\check H^d(\Omega ;\mathbb {R})\rightarrow \check H^d(\Omega ;\mathbb {R})$
gives rates of convergence of ergodic integrals. This was first proved in [Reference SadunSad11] in the self-similar case and later in [Reference Schmieding and TreviñoST18] in the self-affine case. The class of functions used in those results were
![]() $C^\infty _{tlc}$
. Theorem 3.3 implies that the same rates of convergence can now be given for functions in
$C^\infty _{tlc}$
. Theorem 3.3 implies that the same rates of convergence can now be given for functions in
![]() $\mathcal {S}^r_{\alpha }$
for
$\mathcal {S}^r_{\alpha }$
for
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>1$
. The statement will be provided here without proof as Theorem 3.3 allows the argument in [Reference Schmieding and TreviñoST18] to carry over verbatim.
$\alpha>1$
. The statement will be provided here without proof as Theorem 3.3 allows the argument in [Reference Schmieding and TreviñoST18] to carry over verbatim.
Before stating the theorem, some notation needs to be established. Denote by
![]() $|\nu _1|> \cdots > |\nu _r| > 0$
the norms of the r distinct eigenvalues of the map
$|\nu _1|> \cdots > |\nu _r| > 0$
the norms of the r distinct eigenvalues of the map
![]() $\Phi ^{*}$
acting on
$\Phi ^{*}$
acting on
![]() $H^d$
. Let
$H^d$
. Let
![]() $E_i$
be the generalized eigenspaces for the action of
$E_i$
be the generalized eigenspaces for the action of
![]() $\Phi $
on
$\Phi $
on
![]() $H^d(\Omega ;\mathbb {R})$
induced by the map
$H^d(\Omega ;\mathbb {R})$
induced by the map
![]() $\Phi ^{*}$
corresponding to the eigenvalue
$\Phi ^{*}$
corresponding to the eigenvalue
![]() $\nu _i$
. The subspaces
$\nu _i$
. The subspaces
![]() $E_i$
are decomposed as
$E_i$
are decomposed as
 $$ \begin{align*} E_i = \bigoplus_{j=1}^{\kappa(i)} E_{i,j}, \end{align*} $$
$$ \begin{align*} E_i = \bigoplus_{j=1}^{\kappa(i)} E_{i,j}, \end{align*} $$
where
![]() $\kappa (i)$
is the size of the largest Jordan block associated with
$\kappa (i)$
is the size of the largest Jordan block associated with
![]() $\nu _i$
, as follows. For each i, we choose a basis of classes
$\nu _i$
, as follows. For each i, we choose a basis of classes
![]() $\{[\eta _{i,j,k}]\}$
with the property that
$\{[\eta _{i,j,k}]\}$
with the property that
![]() $\langle [\eta _{i,j,1}],[\eta _{i,j,2}],\ldots , [\eta _{i,j,s(i,j)}]\rangle = E_{i,j}$
and
$\langle [\eta _{i,j,1}],[\eta _{i,j,2}],\ldots , [\eta _{i,j,s(i,j)}]\rangle = E_{i,j}$
and
 $$ \begin{align} \Phi^{*} [\eta_{i,j,k}] = \left\{\!\!\begin{array}{ll} \nu_i [\eta_{i,j,k}] + [\eta_{i,j-1,k}] &\mbox{ for } j>1, \\ \nu_i [\eta_{i,j,k}] &\mbox{ for } j=1. \end{array} \right. \end{align} $$
$$ \begin{align} \Phi^{*} [\eta_{i,j,k}] = \left\{\!\!\begin{array}{ll} \nu_i [\eta_{i,j,k}] + [\eta_{i,j-1,k}] &\mbox{ for } j>1, \\ \nu_i [\eta_{i,j,k}] &\mbox{ for } j=1. \end{array} \right. \end{align} $$
Definition 3.8. The rapidly expanding subspace
![]() $E^+(\Omega ) \subset H^d(\Omega )$
is the direct sum of all generalized eigenspaces
$E^+(\Omega ) \subset H^d(\Omega )$
is the direct sum of all generalized eigenspaces
![]() $E_i$
of
$E_i$
of
![]() $\Phi ^{*}$
such that the corresponding eigenvalues
$\Phi ^{*}$
such that the corresponding eigenvalues
![]() $\nu _i$
of
$\nu _i$
of
![]() $\Phi ^{*}$
satisfy
$\Phi ^{*}$
satisfy
The subspace
![]() $E^{++}\subset E^+$
consists of all vectors for which the inequality in equation (17) is strict.
$E^{++}\subset E^+$
consists of all vectors for which the inequality in equation (17) is strict.
We order the indices of distinct subspaces of
![]() $E^+(\Omega )$
as follows. First, we set
$E^+(\Omega )$
as follows. First, we set
![]() $I^+ = I^{+,>} \cup I^{+,=}$
to be the index set of classes
$I^+ = I^{+,>} \cup I^{+,=}$
to be the index set of classes
![]() $[\eta _{i,j,k}]$
which form a generalized eigenbasis for
$[\eta _{i,j,k}]$
which form a generalized eigenbasis for
![]() $E^+(\Omega )$
, where the indices in
$E^+(\Omega )$
, where the indices in
![]() $I^{+,>}$
contain vectors corresponding to a strict inequality in equation (17) and the indices in
$I^{+,>}$
contain vectors corresponding to a strict inequality in equation (17) and the indices in
![]() $I^{+,=}$
correspond to vectors associated to eigenvalues which give an equality in equation (17). The set
$I^{+,=}$
correspond to vectors associated to eigenvalues which give an equality in equation (17). The set
![]() $I^{+,=}$
can be empty but
$I^{+,=}$
can be empty but
![]() $I^{+,>}$
always has at least one element. The set
$I^{+,>}$
always has at least one element. The set
![]() $I^+$
is partially ordered:
$I^+$
is partially ordered:
![]() $(i,j,k)\leq (i',j',k')$
if
$(i,j,k)\leq (i',j',k')$
if
![]() $L(i,j,T)T^{ds_i}\geq L(i',j',T)T^{ds_{i'}}$
for
$L(i,j,T)T^{ds_i}\geq L(i',j',T)T^{ds_{i'}}$
for
![]() $T>1$
, where
$T>1$
, where
 $$ \begin{align} L(i,j,T) = \left\{\!\!\begin{array}{ll} (\log T)^{j-1} &\mbox{if } \nu_i \mbox{ satisfies equation~(17) strictly,} \\ (\log T)^{j} &\mbox{if } \nu_i \mbox{ satisfies equality in equation~(17),} \end{array} \right. \end{align} $$
$$ \begin{align} L(i,j,T) = \left\{\!\!\begin{array}{ll} (\log T)^{j-1} &\mbox{if } \nu_i \mbox{ satisfies equation~(17) strictly,} \\ (\log T)^{j} &\mbox{if } \nu_i \mbox{ satisfies equality in equation~(17),} \end{array} \right. \end{align} $$
and
![]() $s_i = {\log |\nu _i|}/{\log \nu _1}$
. The order does not depend on the indices k.
$s_i = {\log |\nu _i|}/{\log \nu _1}$
. The order does not depend on the indices k.
By passing to a power, we can assume that
![]() $D_\gamma \in GL^+(d,\mathbb {R}) = \mathrm {exp}( \mathfrak {gl}(d,\mathbb {R}))$
. Let
$D_\gamma \in GL^+(d,\mathbb {R}) = \mathrm {exp}( \mathfrak {gl}(d,\mathbb {R}))$
. Let
![]() $a\in \mathfrak {gl}(d,\mathbb {R})$
be the matrix which satisfies
$a\in \mathfrak {gl}(d,\mathbb {R})$
be the matrix which satisfies
![]() $\exp (a) =D_\gamma $
and let
$\exp (a) =D_\gamma $
and let
![]() $g_t = \exp (at)$
. Letting
$g_t = \exp (at)$
. Letting
![]() $B_1$
denote the unit ball, define the averaging family
$B_1$
denote the unit ball, define the averaging family
![]() $\{B_T\}_{T\geq 1}$
by
$\{B_T\}_{T\geq 1}$
by
where
![]() $\sigma = d/\log \det A$
. As such, we have that
$\sigma = d/\log \det A$
. As such, we have that
![]() $\mathrm {Vol}(B_T) = \mathrm {Vol}(B_1) T^d$
. Let
$\mathrm {Vol}(B_T) = \mathrm {Vol}(B_1) T^d$
. Let
![]() $\rho = \mathrm {dim}\, E^+(\Omega _\Lambda )$
.
$\rho = \mathrm {dim}\, E^+(\Omega _\Lambda )$
.
Theorem 3.9. For
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>1$
, there exist a constant
$\alpha>1$
, there exist a constant
![]() $C_{\gamma }$
and
$C_{\gamma }$
and
![]() $\rho $
$\rho $
![]() $\mathbb {R}^d$
-invariant distributions
$\mathbb {R}^d$
-invariant distributions
![]() $\{\mathcal {D}_{i,j,k}\}_{(i,j,k)\in I^+}$
such that, for any
$\{\mathcal {D}_{i,j,k}\}_{(i,j,k)\in I^+}$
such that, for any
![]() $f \in \mathcal {S}^r_{\alpha }(\Omega )$
, if there is an index
$f \in \mathcal {S}^r_{\alpha }(\Omega )$
, if there is an index
![]() $(i,j,k)$
such that
$(i,j,k)$
such that
![]() $\mathcal {D}_{i',j',k'} (f) = 0$
for all
$\mathcal {D}_{i',j',k'} (f) = 0$
for all
![]() $(i',j',k')<(i,j,k)$
but
$(i',j',k')<(i,j,k)$
but
![]() $\mathcal {D}_{i,j,k} (f) \neq 0$
, then for
$\mathcal {D}_{i,j,k} (f) \neq 0$
, then for
![]() $T>3$
and any
$T>3$
and any
![]() $x \in \Omega _{\gamma }$
,
$x \in \Omega _{\gamma }$
,
 $$ \begin{align*} \bigg| \!\int_{B_T} f\circ \varphi_s(x)\,ds \bigg| \leq C_{\gamma,f} L(i,j,T)T^{d ({\log|\nu_{i}|}/{\log \unicode{x3bb}})}. \end{align*} $$
$$ \begin{align*} \bigg| \!\int_{B_T} f\circ \varphi_s(x)\,ds \bigg| \leq C_{\gamma,f} L(i,j,T)T^{d ({\log|\nu_{i}|}/{\log \unicode{x3bb}})}. \end{align*} $$
Moreover, if
![]() $\mathcal {D}_{i,j,k}(f) = 0$
for all
$\mathcal {D}_{i,j,k}(f) = 0$
for all
![]() $(i,j,k)\in I^+_\Lambda $
, then
$(i,j,k)\in I^+_\Lambda $
, then

for all
![]() $T>1$
.
$T>1$
.
4. Ruelle spectrum and quantitative mixing
An application of transverse Hölder cohomology is the construction of anisotropic Banach spaces for solenoids. This section is dedicated to proving the quantitative mixing results for
![]() $\Phi $
. To do this, it is necessary to introduce so-called anisotropic spaces of functions. I am particularly inspired by [Reference Butterley, Kiamari and LiveraniBKL22, Reference Faure, Gouëzel and LanneauFGL19] and the PhD dissertation of D. Galli, and so I will follow some of the ideas there.
$\Phi $
. To do this, it is necessary to introduce so-called anisotropic spaces of functions. I am particularly inspired by [Reference Butterley, Kiamari and LiveraniBKL22, Reference Faure, Gouëzel and LanneauFGL19] and the PhD dissertation of D. Galli, and so I will follow some of the ideas there.
4.1. Anisotropic Banach spaces for flat Wieler solenoids
Let
![]() $\varphi :\Omega \rightarrow \wedge ^kT^{*}\mathbb {R}^d$
be an m-form. Analogous to equation (7), let
$\varphi :\Omega \rightarrow \wedge ^kT^{*}\mathbb {R}^d$
be an m-form. Analogous to equation (7), let
 $$ \begin{align} |\varphi|^{\perp}_{\alpha,m} = \sup_{x\in \Omega_\gamma} \sup_{x\neq y\in C^{\perp}_0(x)}\frac{\| \varphi(x)-\varphi(y)\|}{d(x,y)^\alpha}. \end{align} $$
$$ \begin{align} |\varphi|^{\perp}_{\alpha,m} = \sup_{x\in \Omega_\gamma} \sup_{x\neq y\in C^{\perp}_0(x)}\frac{\| \varphi(x)-\varphi(y)\|}{d(x,y)^\alpha}. \end{align} $$
At first, it may seem like
![]() $\varphi (x)-\varphi (y)$
is not defined, as each summand lives on a different fiber of the bundle. However, since the leaves of the foliation are flat and dense in
$\varphi (x)-\varphi (y)$
is not defined, as each summand lives on a different fiber of the bundle. However, since the leaves of the foliation are flat and dense in
![]() $\Omega $
, parallel transport makes this operation unambiguous. Define the space
$\Omega $
, parallel transport makes this operation unambiguous. Define the space
![]() $H_{\alpha ,m}^{\perp }$
of
$H_{\alpha ,m}^{\perp }$
of
![]() $\alpha $
-Hölder m-forms to be those for which
$\alpha $
-Hölder m-forms to be those for which
This is a Banach space, and if
![]() $\alpha>\beta $
, we have that
$\alpha>\beta $
, we have that
![]() $H^{\perp }_{\alpha ,m}\subset H^{\perp }_{\beta ,m}$
compactly. Denote by
$H^{\perp }_{\alpha ,m}\subset H^{\perp }_{\beta ,m}$
compactly. Denote by
![]() $B_{\varepsilon ,m}^{\perp }(\alpha )\subset H_{\alpha ,m}^{\perp }$
the
$B_{\varepsilon ,m}^{\perp }(\alpha )\subset H_{\alpha ,m}^{\perp }$
the
![]() $\varepsilon $
-ball with respect to equation (22). Note that
$\varepsilon $
-ball with respect to equation (22). Note that
![]() $B_{1,m}^{\perp }(\alpha )\subset B_{1,m}^{\perp }(\alpha -\delta )$
for all
$B_{1,m}^{\perp }(\alpha )\subset B_{1,m}^{\perp }(\alpha -\delta )$
for all
![]() $\delta $
small enough.
$\delta $
small enough.
For the sake of convenience, it will be assumed that
![]() $D_\gamma $
has no Jordan blocks. As such, let
$D_\gamma $
has no Jordan blocks. As such, let
![]() $v_1,\ldots , v_d$
be a normalized basis of
$v_1,\ldots , v_d$
be a normalized basis of
![]() $\mathbb {R}^d$
which are also eigenvectors for
$\mathbb {R}^d$
which are also eigenvectors for
![]() $D_\gamma $
:
$D_\gamma $
:
![]() $D_\gamma v_i = \unicode{x3bb} _i v_i$
with
$D_\gamma v_i = \unicode{x3bb} _i v_i$
with
![]() $\unicode{x3bb} _i>1$
and
$\unicode{x3bb} _i>1$
and
![]() $\unicode{x3bb} = \unicode{x3bb} _1\cdots \unicode{x3bb} _d$
. Given this choice, for any
$\unicode{x3bb} = \unicode{x3bb} _1\cdots \unicode{x3bb} _d$
. Given this choice, for any
![]() $i\in \{1,\ldots , d\}$
,
$i\in \{1,\ldots , d\}$
,
![]() $\partial _i$
will denote the differential operator
$\partial _i$
will denote the differential operator
![]() $\partial _{v_i}$
and for a multiindex
$\partial _{v_i}$
and for a multiindex
![]() $i = (i_1,\ldots , i_d)$
, we will denote by
$i = (i_1,\ldots , i_d)$
, we will denote by
![]() $\partial ^i= \partial ^{i_1}_{1}\cdots \partial ^{i_d}_d$
and
$\partial ^i= \partial ^{i_1}_{1}\cdots \partial ^{i_d}_d$
and
![]() $|i| = i_1+\cdots +i_d$
. With this notation, let
$|i| = i_1+\cdots +i_d$
. With this notation, let

and let
![]() $\mathcal {B}^{r,\alpha }_{m}$
be the completion of
$\mathcal {B}^{r,\alpha }_{m}$
be the completion of
![]() $\Psi ^m_{r,\alpha }$
with respect to
$\Psi ^m_{r,\alpha }$
with respect to ![]() and set
and set
![]() $\Lambda = {\log \unicode{x3bb} }/{\log \unicode{x3bb} _0}$
.
$\Lambda = {\log \unicode{x3bb} }/{\log \unicode{x3bb} _0}$
.
To the uninitiated reader, it is worth pointing out that functions in the anisotropic Banach spaces
![]() $\mathcal {B}_m^{r,\alpha }$
play two simultaneous roles, which become evident from the way the norm was defined: first, they serve as functions in the Euclidean variable; whereas in the transversal variable, they serve the roles of currents.
$\mathcal {B}_m^{r,\alpha }$
play two simultaneous roles, which become evident from the way the norm was defined: first, they serve as functions in the Euclidean variable; whereas in the transversal variable, they serve the roles of currents.
Recall the Hodge-
![]() $\star $
operator which sends m-forms to
$\star $
operator which sends m-forms to
![]() $(d-m)$
forms
$(d-m)$
forms
![]() $\star : \Psi ^m_{r,\alpha }\rightarrow \Psi ^{d-m}_{r,\alpha }$
. The invariant probability measure
$\star : \Psi ^m_{r,\alpha }\rightarrow \Psi ^{d-m}_{r,\alpha }$
. The invariant probability measure
![]() $\mu $
gives a canonical choice of the Lebesgue volume element on the
$\mu $
gives a canonical choice of the Lebesgue volume element on the
![]() $\mathbb {R}^d$
-leaves of
$\mathbb {R}^d$
-leaves of
![]() $\Omega $
, and thus there is a canonical volume element
$\Omega $
, and thus there is a canonical volume element
![]() $dt = \star 1$
. With this choice, the Hodge-
$dt = \star 1$
. With this choice, the Hodge-
![]() $\star $
operator gives a canonical bijection between functions and tangential d-forms: for
$\star $
operator gives a canonical bijection between functions and tangential d-forms: for
![]() $h\in \mathcal {S}^r_{\alpha }$
,
$h\in \mathcal {S}^r_{\alpha }$
,
![]() $\star h = h(\star 1) = h\, dt\in \Psi ^d_{r,\alpha }$
.
$\star h = h(\star 1) = h\, dt\in \Psi ^d_{r,\alpha }$
.
Proposition 4.1.
![]() $\mathcal {B}^{r',\alpha '}_{m}\subset \mathcal {B}^{r,\alpha }_{m}$
if
$\mathcal {B}^{r',\alpha '}_{m}\subset \mathcal {B}^{r,\alpha }_{m}$
if
![]() $r'\geq r$
and
$r'\geq r$
and
![]() $\alpha '\leq \alpha $
, and the inclusion is compact if
$\alpha '\leq \alpha $
, and the inclusion is compact if
![]() $r'>r$
and
$r'>r$
and
![]() $\alpha>\alpha '+\Lambda >\Lambda >0$
.
$\alpha>\alpha '+\Lambda >\Lambda >0$
.
The inclusions follow from the definitions of the norms so what is left to prove is the compactness of the inclusion. The following compactness criterion [Reference Faure, Gouëzel and LanneauFGL19, §2.2] will be used: let
![]() $\mathcal {B}\subset \mathcal {C}$
be two Banach spaces and assume that for any
$\mathcal {B}\subset \mathcal {C}$
be two Banach spaces and assume that for any
![]() $\varepsilon>0$
, there exist finitely many continuous linear forms
$\varepsilon>0$
, there exist finitely many continuous linear forms
![]() $L_1,\ldots , L_m$
on
$L_1,\ldots , L_m$
on
![]() $\mathcal {B}$
such that for any
$\mathcal {B}$
such that for any
![]() $x\in \mathcal {B}$
,
$x\in \mathcal {B}$
,
Then the inclusion of
![]() $\mathcal {B}$
in
$\mathcal {B}$
in
![]() $\mathcal {C}$
is compact.
$\mathcal {C}$
is compact.
To apply the criterion, several estimates will need to be obtained. For an m-form
![]() $\varphi :\Omega \rightarrow \wedge ^m T^{*}\mathbb {R}^d$
and
$\varphi :\Omega \rightarrow \wedge ^m T^{*}\mathbb {R}^d$
and
![]() $k\in \mathbb {N}_0$
, set
$k\in \mathbb {N}_0$
, set
![]() $\hat \nu _{k,x}:=\nu _{k,x}(C^{\perp }_k(x))$
, recall equation (11):
$\hat \nu _{k,x}:=\nu _{k,x}(C^{\perp }_k(x))$
, recall equation (11):
 $$ \begin{align} \Pi_k\varphi(x):= \hat\nu_{k,x}^{-1}\int_{C_k^{\perp}(x)} \varphi\,d\nu_{k,x}\quad \mbox{and}\quad\Delta_k:= \varphi-\Pi_k\varphi, \end{align} $$
$$ \begin{align} \Pi_k\varphi(x):= \hat\nu_{k,x}^{-1}\int_{C_k^{\perp}(x)} \varphi\,d\nu_{k,x}\quad \mbox{and}\quad\Delta_k:= \varphi-\Pi_k\varphi, \end{align} $$
both of which are m-forms. Recall that
![]() $\Pi _k\varphi $
is transversally locally constant. That is,
$\Pi _k\varphi $
is transversally locally constant. That is,
![]() $\Pi _k\varphi (z)$
depends only on the first k coordinates
$\Pi _k\varphi (z)$
depends only on the first k coordinates
![]() $z_i$
of z.
$z_i$
of z.
Lemma 4.2. For
![]() $r\in \mathbb {N}_0$
, let
$r\in \mathbb {N}_0$
, let
![]() $\varphi :\Omega \rightarrow \wedge ^m T^{*}\mathbb {R}^d$
with
$\varphi :\Omega \rightarrow \wedge ^m T^{*}\mathbb {R}^d$
with
![]() $\|\varphi \|^{\perp }_{\alpha +r,m}\leq 1$
. If
$\|\varphi \|^{\perp }_{\alpha +r,m}\leq 1$
. If
![]() $\alpha>\Lambda +\alpha '>0$
, then for any
$\alpha>\Lambda +\alpha '>0$
, then for any
![]() $\varepsilon>0$
, there exists a
$\varepsilon>0$
, there exists a
![]() $k>0$
such that
$k>0$
such that

Proof. Using Lemma 2.1,

and so
![]() $\|\Delta _k\varphi \|_{C^0}\leq 2 C_\varphi \unicode{x3bb} _0^{-(\alpha +r)k}$
.
$\|\Delta _k\varphi \|_{C^0}\leq 2 C_\varphi \unicode{x3bb} _0^{-(\alpha +r)k}$
.
Now
![]() $\|\Delta _k\varphi \|_{\alpha ',m}^{\perp }$
will be bound. If
$\|\Delta _k\varphi \|_{\alpha ',m}^{\perp }$
will be bound. If
![]() $a,b\in C^{\perp }_\ell (x)$
with
$a,b\in C^{\perp }_\ell (x)$
with
![]() $\ell \geq k$
, then
$\ell \geq k$
, then
![]() $C^{\perp }_k(a) = C_k^{\perp }(b)$
and so
$C^{\perp }_k(a) = C_k^{\perp }(b)$
and so

If
![]() $\ell <k$
and
$\ell <k$
and
![]() $a,b\in C^{\perp }_\ell (x)$
,
$a,b\in C^{\perp }_\ell (x)$
,

Thus, if
![]() $a,b\in C_\ell ^{\perp }(x)$
,
$a,b\in C_\ell ^{\perp }(x)$
,

Putting everything together:

Thus, if

then
![]() $\|\Delta _k\varphi \|^{\perp }_{\alpha '+r,m}\leq \varepsilon /2$
, which proves the first estimate.
$\|\Delta _k\varphi \|^{\perp }_{\alpha '+r,m}\leq \varepsilon /2$
, which proves the first estimate.
To obtain the second estimate, first note that for
![]() $a,b\in C^{\perp }_\ell (x)$
,
$a,b\in C^{\perp }_\ell (x)$
,
![]() $\|\Pi _k\varphi (a)-\Pi _k\varphi (b)\| = 0$
if
$\|\Pi _k\varphi (a)-\Pi _k\varphi (b)\| = 0$
if
![]() $\ell \geq k$
and if
$\ell \geq k$
and if
![]() $\ell <k$
,
$\ell <k$
,

where the first estimate follows from the fact that
![]() $\|\varphi \|^{\perp }_{r+\alpha ,m}\leq 1$
and the second from the estimate leading to equation (24). Thus,
$\|\varphi \|^{\perp }_{r+\alpha ,m}\leq 1$
and the second from the estimate leading to equation (24). Thus,
and so it follows that
Using in equation (26) the choice for k in equation (25), the second estimate follows.
Proof of Proposition 4.1
To apply the compactness criterion, let
![]() $\varepsilon>0$
. Since
$\varepsilon>0$
. Since
![]() $H^{\perp }_{\alpha +r,m}$
is compactly embedded in
$H^{\perp }_{\alpha +r,m}$
is compactly embedded in
![]() $H^{\perp }_{\alpha '+r,m}$
, let
$H^{\perp }_{\alpha '+r,m}$
, let
![]() $\{\varphi _j\}_{j\leq K_{\varepsilon }}\subset H^{\perp }_{\alpha +r,m}$
be a finite family of forms such that for any
$\{\varphi _j\}_{j\leq K_{\varepsilon }}\subset H^{\perp }_{\alpha +r,m}$
be a finite family of forms such that for any
![]() $\varphi \in H^{\perp }_{\alpha +r,m}$
with
$\varphi \in H^{\perp }_{\alpha +r,m}$
with
![]() $\|\varphi _j\|^{\perp }_{\alpha +r,m}\leq 4\unicode{x3bb} _0^\Lambda C_\mu ({8C_\mu }/{\varepsilon })^{{\Lambda }/{r+\alpha -\Lambda -\alpha '}}$
, there is a
$\|\varphi _j\|^{\perp }_{\alpha +r,m}\leq 4\unicode{x3bb} _0^\Lambda C_\mu ({8C_\mu }/{\varepsilon })^{{\Lambda }/{r+\alpha -\Lambda -\alpha '}}$
, there is a
![]() $\varphi _{j^{*}}$
in the family such that
$\varphi _{j^{*}}$
in the family such that
![]() $\|\varphi -\varphi _{j^{*}}\|_{\alpha '+r,m}^{\perp }\leq \varepsilon /2$
. Define the finite family of linear forms
$\|\varphi -\varphi _{j^{*}}\|_{\alpha '+r,m}^{\perp }\leq \varepsilon /2$
. Define the finite family of linear forms
![]() $L_{j,i}:\mathcal {B}^{r',\alpha '}_m\rightarrow \mathbb {R}$
by
$L_{j,i}:\mathcal {B}^{r',\alpha '}_m\rightarrow \mathbb {R}$
by
where i is a multiindex of length at most
![]() $r'$
and
$r'$
and
![]() $j\leq K_{\varepsilon }$
.
$j\leq K_{\varepsilon }$
.
For
![]() $\varphi $
with
$\varphi $
with
![]() $\|\varphi \|^{\perp }_{\alpha +r,m}\leq 1$
, let
$\|\varphi \|^{\perp }_{\alpha +r,m}\leq 1$
, let
![]() $k\in \mathbb {N}$
be the one given by Lemma 4.2, so that
$k\in \mathbb {N}$
be the one given by Lemma 4.2, so that
![]() $\|\Delta _k\varphi \|^{\perp }_{\alpha '+r,m}\leq \varepsilon /2$
. Let
$\|\Delta _k\varphi \|^{\perp }_{\alpha '+r,m}\leq \varepsilon /2$
. Let
![]() $j^{*}\leq K_{\varepsilon }$
be such that
$j^{*}\leq K_{\varepsilon }$
be such that
![]() $\|\Pi _k\varphi -\varphi _{j^{*}}\|^{\perp }_{\alpha '+r,m}\leq \varepsilon /2$
. Thus, for
$\|\Pi _k\varphi -\varphi _{j^{*}}\|^{\perp }_{\alpha '+r,m}\leq \varepsilon /2$
. Thus, for
![]() $\eta \in \mathcal {B}^{r',\alpha '}_m$
and a multiindex i with
$\eta \in \mathcal {B}^{r',\alpha '}_m$
and a multiindex i with
![]() $|i|=r$
, it follows that
$|i|=r$
, it follows that
 $$ \begin{align*}\bigg|\!\int_\Omega \langle \varphi, \partial^i \eta\rangle\, d\mu\bigg|\leq \bigg|\!\int_\Omega\langle \Delta_k\varphi ,\partial^i\eta\rangle\, d\mu\bigg| + \bigg|\!\int_\Omega \langle\Pi_k\varphi-\varphi_{j^{*}},\partial^i\eta\rangle\, d\mu\bigg| + \bigg|\!\int_\Omega \langle \varphi_{j^{*}},\partial^i\eta\rangle\,d\mu\bigg|, \end{align*} $$
$$ \begin{align*}\bigg|\!\int_\Omega \langle \varphi, \partial^i \eta\rangle\, d\mu\bigg|\leq \bigg|\!\int_\Omega\langle \Delta_k\varphi ,\partial^i\eta\rangle\, d\mu\bigg| + \bigg|\!\int_\Omega \langle\Pi_k\varphi-\varphi_{j^{*}},\partial^i\eta\rangle\, d\mu\bigg| + \bigg|\!\int_\Omega \langle \varphi_{j^{*}},\partial^i\eta\rangle\,d\mu\bigg|, \end{align*} $$
and so it follows that
and so compactness follows from the criterion.
It will be useful below to have a version of cohomology with coefficients in the anisotropic spaces
![]() $\mathcal {B}_*^{r,\alpha }$
. To that end, let
$\mathcal {B}_*^{r,\alpha }$
. To that end, let
![]() $H_{\mathcal {B}^{r,\alpha }}^{*}(\Omega )$
be the cohomology of tangentially smooth forms with
$H_{\mathcal {B}^{r,\alpha }}^{*}(\Omega )$
be the cohomology of tangentially smooth forms with
![]() $\mathcal {B}^{r,\alpha }_0$
coefficients.
$\mathcal {B}^{r,\alpha }_0$
coefficients.
Proposition 4.3. Let
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>1$
. Then
$\alpha>1$
. Then
![]() $H_{\mathcal {B}^{r,\alpha }}^{*}(\Omega )\cong \mathcal {H}^{*}_{r,\alpha }(\Omega ) \cong \check H(\Omega ;\mathbb {R})$
.
$H_{\mathcal {B}^{r,\alpha }}^{*}(\Omega )\cong \mathcal {H}^{*}_{r,\alpha }(\Omega ) \cong \check H(\Omega ;\mathbb {R})$
.
Proof. Let
![]() $\eta \in \mathcal {B}_m^{r,\alpha }$
be a closed m-form. It will be shown that there is a form
$\eta \in \mathcal {B}_m^{r,\alpha }$
be a closed m-form. It will be shown that there is a form
![]() $\eta '\in \Psi ^m_{r,\alpha }$
such that
$\eta '\in \Psi ^m_{r,\alpha }$
such that
![]() $\eta -\eta ' = d\omega $
.
$\eta -\eta ' = d\omega $
.
Let
![]() $\{\eta _k\}\subset \Psi ^m_{r,\alpha }$
be a sequence of closed forms such that
$\{\eta _k\}\subset \Psi ^m_{r,\alpha }$
be a sequence of closed forms such that
![]() $\eta _k\rightarrow \eta $
in
$\eta _k\rightarrow \eta $
in
![]() $\mathcal {B}_m^{r,\alpha }$
. As in the proof of Proposition 3.7, for each k, there is an
$\mathcal {B}_m^{r,\alpha }$
. As in the proof of Proposition 3.7, for each k, there is an
![]() $\eta ^{\prime }_k\in \pi ^{*}_{\beta _m} C^r(\Gamma )$
such that
$\eta ^{\prime }_k\in \pi ^{*}_{\beta _m} C^r(\Gamma )$
such that
![]() $\eta _k - \eta _k^{\prime } = d\omega _k$
. Thus,
$\eta _k - \eta _k^{\prime } = d\omega _k$
. Thus,
for any
![]() $\varphi \in H^{\perp }_{\alpha }(\Omega )$
. Thus,
$\varphi \in H^{\perp }_{\alpha }(\Omega )$
. Thus,
![]() $[\eta -\eta ^{\prime }_k] = [\eta ]-[\eta ^{\prime }_k]\rightarrow 0$
. However,
$[\eta -\eta ^{\prime }_k] = [\eta ]-[\eta ^{\prime }_k]\rightarrow 0$
. However,
![]() $\eta ^{\prime }_k\in \pi ^{*}_{\beta _m}C^r$
for all k, and so
$\eta ^{\prime }_k\in \pi ^{*}_{\beta _m}C^r$
for all k, and so
![]() $[\eta ^{\prime }_k]\in \pi ^{*}_{\beta _m}\check H^m(\Gamma ;\mathbb {R})\subset \check H^m(\Omega ;\mathbb {R})$
for all k, meaning that
$[\eta ^{\prime }_k]\in \pi ^{*}_{\beta _m}\check H^m(\Gamma ;\mathbb {R})\subset \check H^m(\Omega ;\mathbb {R})$
for all k, meaning that
![]() $[\eta ]$
defines a class in
$[\eta ]$
defines a class in
![]() $\check H^m(\Omega ;\mathbb {R})$
.
$\check H^m(\Omega ;\mathbb {R})$
.
Proposition 2.3 and the definition of the spaces
![]() $\mathcal {B}_m^{r,\alpha }$
implies the following.
$\mathcal {B}_m^{r,\alpha }$
implies the following.
Lemma 4.4. The differential operator d on m forms is a bounded operator from
![]() $\mathcal {B}^{r,\alpha }_m$
to
$\mathcal {B}^{r,\alpha }_m$
to
![]() $\mathcal {B}^{r-1,\alpha +1}_{m+1}$
.
$\mathcal {B}^{r-1,\alpha +1}_{m+1}$
.
4.2. The transfer operator
Define the transfer operator to be
where f is an m-form and note that for any
![]() $y\in C_0^{\perp }(x)$
,
$y\in C_0^{\perp }(x)$
,
and so
The following estimates, similar to those of Lemma 4.2, will be needed in the proof for the Lasota–Yorke inequalities below.
Lemma 4.5. If
![]() $\|\varphi \|^{\perp }_{\beta ,m}\leq 1$
, then for
$\|\varphi \|^{\perp }_{\beta ,m}\leq 1$
, then for
![]() $\alpha>\beta $
,
$\alpha>\beta $
,

Proof. The estimate for
![]() $\|\Delta _k\varphi \|^{\perp }_{\beta ,m}$
follows essentially from the computations up to and including equation (24), and combined with equation (27), the estimate for
$\|\Delta _k\varphi \|^{\perp }_{\beta ,m}$
follows essentially from the computations up to and including equation (24), and combined with equation (27), the estimate for
![]() $\|(\Delta _k\varphi )\circ \Phi ^n\|^{\perp }_{\beta ,m}$
follows. Now, if
$\|(\Delta _k\varphi )\circ \Phi ^n\|^{\perp }_{\beta ,m}$
follows. Now, if
![]() $a,b\in C^{\perp }_\ell (x)$
and
$a,b\in C^{\perp }_\ell (x)$
and
![]() $\ell \geq k$
, then
$\ell \geq k$
, then
![]() $\|\Pi _k\varphi (a)-\Pi _k\varphi (b)\|=0$
. If
$\|\Pi _k\varphi (a)-\Pi _k\varphi (b)\|=0$
. If
![]() $\ell <k$
,
$\ell <k$
,
where the last term is obtained in the same way as the estimates leading to equation (24), and so
![]() $|\Pi _k\varphi |^{\perp }_{\alpha ,m}\leq 3C_\mu \unicode{x3bb} _0^{(\alpha -\beta )k}$
, which combined with equation (27) proves the estimate for
$|\Pi _k\varphi |^{\perp }_{\alpha ,m}\leq 3C_\mu \unicode{x3bb} _0^{(\alpha -\beta )k}$
, which combined with equation (27) proves the estimate for
![]() $\|\Pi _k\varphi \circ \Phi ^n\|^{\perp }_{\alpha ,m}$
.
$\|\Pi _k\varphi \circ \Phi ^n\|^{\perp }_{\alpha ,m}$
.
Proposition 4.6. (Lasota–Yorke inequalities)
For each
![]() $r,n\in \mathbb {N}$
,
$r,n\in \mathbb {N}$
,
![]() $\alpha ,\alpha '$
with
$\alpha ,\alpha '$
with
![]() $\alpha>\alpha '>0$
,
$\alpha>\alpha '>0$
,
![]() $\nu \in (\unicode{x3bb} _0^{-r},1)$
, and
$\nu \in (\unicode{x3bb} _0^{-r},1)$
, and
![]() $m\in \{0,\ldots , d\}$
, there are
$m\in \{0,\ldots , d\}$
, there are
![]() $D,E>0$
such that
$D,E>0$
such that
Proof. First observe that

This combined with equation (27) yields the first inequality. To address the second, first note that

and so equation (29) implies that
Now, if
![]() $\|\varphi \|^{\perp }_{\alpha '+p,m}\leq 1$
and
$\|\varphi \|^{\perp }_{\alpha '+p,m}\leq 1$
and
![]() $|i|=p\leq r$
, again by equation (29),
$|i|=p\leq r$
, again by equation (29),

and so using Lemma 4.5,

Combining these estimates with equation (30),

from which the result follows.
4.3. The spectrum of
 $\mathcal {L}$
$\mathcal {L}$
Propositions 4.1 and 4.6, combined with Hennion’s theorem [Reference Demers, Kiamari and LiveraniDKL21, Theorem B.14], yields the following corollary.
Corollary 4.7. For
![]() $\alpha>\Lambda $
and
$\alpha>\Lambda $
and
![]() $r\in \mathbb {N}$
, the spectrum of
$r\in \mathbb {N}$
, the spectrum of
![]() $\mathcal {L}:\mathcal {B}^{r,\alpha }_m\rightarrow \mathcal {B}^{r,\alpha }_m$
is contained in the closed unit ball in
$\mathcal {L}:\mathcal {B}^{r,\alpha }_m\rightarrow \mathcal {B}^{r,\alpha }_m$
is contained in the closed unit ball in
![]() $\mathbb {C}$
and the essential spectrum is contained in the closed ball of radius
$\mathbb {C}$
and the essential spectrum is contained in the closed ball of radius
![]() $\unicode{x3bb} _0^{-r}$
in
$\unicode{x3bb} _0^{-r}$
in
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
The following Proposition is a consequence of a theorem of Baladi and Tsuji, and shows that to a certain extent, the spectrum is independent of Banach spaces used.
Proposition 4.8. The discrete spectrum is independent of the Banach space
![]() $\mathcal {B}_0^{r,\alpha }$
: for
$\mathcal {B}_0^{r,\alpha }$
: for
![]() $\alpha>\Lambda $
and
$\alpha>\Lambda $
and
![]() $r'>r>0$
, then the discrete part of the spectrum of
$r'>r>0$
, then the discrete part of the spectrum of
![]() $\mathcal {L}$
of norm greater than
$\mathcal {L}$
of norm greater than
![]() $\unicode{x3bb} _0^{-r}$
coincides for
$\unicode{x3bb} _0^{-r}$
coincides for
![]() $\mathcal {L}|_{\mathcal {B}_0^{r,\alpha }}$
and
$\mathcal {L}|_{\mathcal {B}_0^{r,\alpha }}$
and
![]() $\mathcal {L}|_{\mathcal {B}_0^{r',\alpha }}$
. In addition, the corresponding generalized eigenspaces are contained in
$\mathcal {L}|_{\mathcal {B}_0^{r',\alpha }}$
. In addition, the corresponding generalized eigenspaces are contained in
![]() $\mathcal {B}_0^{r,\alpha }\cap \mathcal {B}_0^{r',\alpha }$
.
$\mathcal {B}_0^{r,\alpha }\cap \mathcal {B}_0^{r',\alpha }$
.
Proof. The results will follow from [Reference Baladi, Tsujii, Burns, Dolgopyat and PesinBT08, Lemma A.1] as long as the inclusion
![]() $\mathcal {S}_{\alpha }^{r'}\subset \mathcal {S}^r_{\alpha }$
is shown to be dense with respect to
$\mathcal {S}_{\alpha }^{r'}\subset \mathcal {S}^r_{\alpha }$
is shown to be dense with respect to ![]() .
.
Write
![]() $f = \sum _{k\geq 0}f^{(k)}\in \mathcal {S}^r_{\alpha }$
in the canonical way, where
$f = \sum _{k\geq 0}f^{(k)}\in \mathcal {S}^r_{\alpha }$
in the canonical way, where
![]() $f^{(k)} = \pi ^{*}_k g_k$
for some
$f^{(k)} = \pi ^{*}_k g_k$
for some
![]() $g_k\in C^r(\Gamma _k)$
as described in §2.1. Since smooth functions are dense in
$g_k\in C^r(\Gamma _k)$
as described in §2.1. Since smooth functions are dense in
![]() $C^r(\Gamma _k)$
, for every
$C^r(\Gamma _k)$
, for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $k\in \mathbb {N}_0$
, pick a
$k\in \mathbb {N}_0$
, pick a
![]() $g_{n,k}\in C^{r'}(\Gamma _k)$
such that
$g_{n,k}\in C^{r'}(\Gamma _k)$
such that
![]() $\|g_k-g_{n,k}\|_{C^r(\Gamma _k)}\leq \unicode{x3bb} _0^{-(n+\alpha k)}$
. Let
$\|g_k-g_{n,k}\|_{C^r(\Gamma _k)}\leq \unicode{x3bb} _0^{-(n+\alpha k)}$
. Let
![]() $f_n:= \sum _{k\geq 0} \pi ^{*}_kg_{n,k}$
. It now needs to be shown that
$f_n:= \sum _{k\geq 0} \pi ^{*}_kg_{n,k}$
. It now needs to be shown that
![]() $f_n\rightarrow f$
in
$f_n\rightarrow f$
in
![]() $\mathcal {B}_0^{r,\alpha }$
.
$\mathcal {B}_0^{r,\alpha }$
.
If
![]() $\varphi \in L^1$
and
$\varphi \in L^1$
and
![]() $\|\varphi \|_\infty \leq 1$
,
$\|\varphi \|_\infty \leq 1$
,

and thus ![]() and the statement follows from [Reference Baladi, Tsujii, Burns, Dolgopyat and PesinBT08, Lemma A.1].
and the statement follows from [Reference Baladi, Tsujii, Burns, Dolgopyat and PesinBT08, Lemma A.1].
Denote by
![]() $\Sigma _m^+$
the spectrum of
$\Sigma _m^+$
the spectrum of
![]() $\Phi ^{*}:\check H^m(\Omega ;\mathbb {R})\rightarrow \check H^m(\Omega ;\mathbb {R})$
consisting of expanding eigenvalues,
$\Phi ^{*}:\check H^m(\Omega ;\mathbb {R})\rightarrow \check H^m(\Omega ;\mathbb {R})$
consisting of expanding eigenvalues,
![]() $\Sigma _m^-$
the spectrum of
$\Sigma _m^-$
the spectrum of
![]() $\Phi ^{-1*}:\check H^m(\Omega ;\mathbb {R})\rightarrow \check H^m(\Omega ;\mathbb {R})$
consisting of contracting eigenvalues, and set
$\Phi ^{-1*}:\check H^m(\Omega ;\mathbb {R})\rightarrow \check H^m(\Omega ;\mathbb {R})$
consisting of contracting eigenvalues, and set
to be the discrete spectrum of
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $\mathcal {B}^{r,\alpha }_m$
, assuming
$\mathcal {B}^{r,\alpha }_m$
, assuming
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>\Lambda $
by Corollary 4.7. Note that the map
$\alpha>\Lambda $
by Corollary 4.7. Note that the map
![]() $x\mapsto x^{-1}$
gives a bijection between
$x\mapsto x^{-1}$
gives a bijection between
![]() $\Sigma _m^+$
and
$\Sigma _m^+$
and
![]() $\Sigma _m^-$
.
$\Sigma _m^-$
.
Lemma 4.9. For
![]() $\alpha>\Lambda $
,
$\alpha>\Lambda $
,
![]() $r\in \mathbb {N}$
, and
$r\in \mathbb {N}$
, and
![]() $\sigma _{r,\alpha , m}$
as above:
$\sigma _{r,\alpha , m}$
as above:
-
(i)
 $1\in \sigma _{r,\alpha ,0}$
; it is the unique eigenvalue of modulus 1 and it has multiplicity one;
$1\in \sigma _{r,\alpha ,0}$
; it is the unique eigenvalue of modulus 1 and it has multiplicity one; -
(ii)
 $\nu \in \sigma _{r,\alpha ,0}$
if and only if
$\nu \in \sigma _{r,\alpha ,0}$
if and only if
 $\unicode{x3bb} ^{-1}\nu \in \sigma _{r,\alpha ,d}$
;
$\unicode{x3bb} ^{-1}\nu \in \sigma _{r,\alpha ,d}$
; -
(iii) for
 $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
 $\alpha>\Lambda +1$
,
$\alpha>\Lambda +1$
,
 $\Sigma _d^-\setminus \sigma _{r+1,\alpha -1,d-1}\subset \sigma _{r,\alpha ,d}$
;
$\Sigma _d^-\setminus \sigma _{r+1,\alpha -1,d-1}\subset \sigma _{r,\alpha ,d}$
; -
(iv)
 $\Sigma _d^-\setminus \{\unicode{x3bb} ^{-1}\}\subset \sigma _{r,\alpha , d-1}$
;
$\Sigma _d^-\setminus \{\unicode{x3bb} ^{-1}\}\subset \sigma _{r,\alpha , d-1}$
; -
(v)
 $\sigma _{r,\alpha , m}\subset (\sigma _{r+1,\alpha -1,m-1}\cup \Sigma _m^-\cup \sigma _{r-1,\alpha +1,m+1})$
.
$\sigma _{r,\alpha , m}\subset (\sigma _{r+1,\alpha -1,m-1}\cup \Sigma _m^-\cup \sigma _{r-1,\alpha +1,m+1})$
.
Proof. The map
![]() $\Phi $
is topologically mixing [Reference Anderson and PutnamAP98, Proposition 3.1]. Property (i) follows from a standard argument depending on this mixing hypothesis; see [Reference DemersDem18, §4.1] or [Reference BaladiBal18, §7.1.1]. Item (ii) follows from the duality between 0 and d forms given by the Hodge-
$\Phi $
is topologically mixing [Reference Anderson and PutnamAP98, Proposition 3.1]. Property (i) follows from a standard argument depending on this mixing hypothesis; see [Reference DemersDem18, §4.1] or [Reference BaladiBal18, §7.1.1]. Item (ii) follows from the duality between 0 and d forms given by the Hodge-
![]() $\star $
operator.
$\star $
operator.
For property (iii), it needs to be shown that if
![]() $\nu \in \Sigma _d^-$
and
$\nu \in \Sigma _d^-$
and
![]() $\nu \not \in \sigma _{r+1,\alpha -1,d-1}$
, then there exists a
$\nu \not \in \sigma _{r+1,\alpha -1,d-1}$
, then there exists a
![]() $\eta \in \Psi ^d_{r,\alpha }$
such that
$\eta \in \Psi ^d_{r,\alpha }$
such that
![]() $(\mathcal {L}-\nu \cdot \mathrm {Id})^k\eta = 0$
for some
$(\mathcal {L}-\nu \cdot \mathrm {Id})^k\eta = 0$
for some
![]() $k\geq 0$
. Now, if
$k\geq 0$
. Now, if
![]() $\nu \in \Sigma _d^-\setminus \sigma _{r+1,\alpha -1,d-1}$
, then by Theorem 3.3, there exists
$\nu \in \Sigma _d^-\setminus \sigma _{r+1,\alpha -1,d-1}$
, then by Theorem 3.3, there exists
![]() $\eta \in \Psi ^d_{r,\alpha }$
such that
$\eta \in \Psi ^d_{r,\alpha }$
such that
![]() $(\mathcal {L}-\nu \cdot \mathrm {Id})^k[\eta ] = 0$
for all k large enough and so there is an
$(\mathcal {L}-\nu \cdot \mathrm {Id})^k[\eta ] = 0$
for all k large enough and so there is an
![]() $\omega _\eta \in \Psi ^{d-1}_{r+1,\alpha -1}$
such that
$\omega _\eta \in \Psi ^{d-1}_{r+1,\alpha -1}$
such that
![]() $(\mathcal {L}-\nu \cdot \mathrm {Id})^k\eta = d\omega _\eta $
. If
$(\mathcal {L}-\nu \cdot \mathrm {Id})^k\eta = d\omega _\eta $
. If
![]() $\theta = (\mathcal {L}-\nu \cdot \mathrm {Id} )^{-k}\omega _\eta \in \Psi ^{d-1}_{r+1,\alpha -1}$
, then
$\theta = (\mathcal {L}-\nu \cdot \mathrm {Id} )^{-k}\omega _\eta \in \Psi ^{d-1}_{r+1,\alpha -1}$
, then
![]() $\eta ' = \eta -d\theta $
satisfies
$\eta ' = \eta -d\theta $
satisfies
![]() $(\mathcal {L}-\nu \cdot \mathrm {Id})^k\eta ' = 0$
.
$(\mathcal {L}-\nu \cdot \mathrm {Id})^k\eta ' = 0$
.
For item (iv), note that the smallest element (in norm) of
![]() $\Sigma ^-_d$
is
$\Sigma ^-_d$
is
![]() $\unicode{x3bb} ^{-1}$
. Suppose that for some
$\unicode{x3bb} ^{-1}$
. Suppose that for some
![]() $\nu \in \Sigma ^-_d$
with
$\nu \in \Sigma ^-_d$
with
![]() $\unicode{x3bb} ^{-1}< \nu $
,
$\unicode{x3bb} ^{-1}< \nu $
,
![]() $\nu \not \in \sigma _{r,\alpha , d-1}$
. Then by property (iii),
$\nu \not \in \sigma _{r,\alpha , d-1}$
. Then by property (iii),
![]() $\nu \in \sigma _{r-1,\alpha +1, d}$
, which by property (ii) means that
$\nu \in \sigma _{r-1,\alpha +1, d}$
, which by property (ii) means that
![]() $\unicode{x3bb} \nu \in \sigma _{r-1,\alpha +1, 0}$
. However,
$\unicode{x3bb} \nu \in \sigma _{r-1,\alpha +1, 0}$
. However,
![]() $|\unicode{x3bb} \nu |>1$
, contradicting that the spectral radius is 1. So
$|\unicode{x3bb} \nu |>1$
, contradicting that the spectral radius is 1. So
![]() $\nu \in \sigma _{r,\alpha , d-1}$
.
$\nu \in \sigma _{r,\alpha , d-1}$
.
Item (v) is due to Daniele Galli, but the proof is included here for completeness. Let
![]() $\nu \in \sigma _{r,\alpha , m}$
. Then there exists an
$\nu \in \sigma _{r,\alpha , m}$
. Then there exists an
![]() $\eta \in \Psi ^m_{r,\alpha }$
and J such that
$\eta \in \Psi ^m_{r,\alpha }$
and J such that
![]() $(\mathcal {L}-\nu )^J\eta = 0$
. If
$(\mathcal {L}-\nu )^J\eta = 0$
. If
![]() $\eta $
is not closed, then
$\eta $
is not closed, then
![]() $(\mathcal {L}-\nu )^Jd\eta = d(\mathcal {L}-\nu )^J\eta = 0$
, meaning that
$(\mathcal {L}-\nu )^Jd\eta = d(\mathcal {L}-\nu )^J\eta = 0$
, meaning that
![]() $\nu \in \sigma _{r-1,\alpha +1,m+1}$
. Now suppose that
$\nu \in \sigma _{r-1,\alpha +1,m+1}$
. Now suppose that
![]() $\eta $
is closed and not exact. Then
$\eta $
is closed and not exact. Then
![]() $(\mathcal {L}-\nu )^J\eta = 0$
implies that
$(\mathcal {L}-\nu )^J\eta = 0$
implies that
![]() $\nu \in \Sigma _m^-$
. Now suppose that
$\nu \in \Sigma _m^-$
. Now suppose that
![]() $\eta = d\theta \neq 0$
for some
$\eta = d\theta \neq 0$
for some
![]() $\theta \in \Psi ^{m-1}_{r+1,\alpha -1}$
. Then
$\theta \in \Psi ^{m-1}_{r+1,\alpha -1}$
. Then
![]() $(\mathcal {L}-\nu )^J\eta = (\mathcal {L}-\nu )^Jd\theta = d(\mathcal {L}-\nu )^J\theta =0 $
, that is, either
$(\mathcal {L}-\nu )^J\eta = (\mathcal {L}-\nu )^Jd\theta = d(\mathcal {L}-\nu )^J\theta =0 $
, that is, either
![]() $\nu \in \sigma _{r+1,\alpha -1,m-1}$
or
$\nu \in \sigma _{r+1,\alpha -1,m-1}$
or
![]() $(\mathcal {L}-\nu )^J\theta $
is closed. Suppose
$(\mathcal {L}-\nu )^J\theta $
is closed. Suppose
![]() $(\mathcal {L}-\nu )^J\theta $
is closed, set
$(\mathcal {L}-\nu )^J\theta $
is closed, set
![]() $\omega :=(\mathcal {L}-\nu )^J\theta \in \Psi ^{m-1}_{r+1,\alpha -1}$
. If
$\omega :=(\mathcal {L}-\nu )^J\theta \in \Psi ^{m-1}_{r+1,\alpha -1}$
. If
![]() $(\mathcal {L}-\nu )^J$
is invertible on closed forms, then
$(\mathcal {L}-\nu )^J$
is invertible on closed forms, then
![]() $\theta = (\mathcal {L}-\nu )^{-J}\omega $
is closed, and
$\theta = (\mathcal {L}-\nu )^{-J}\omega $
is closed, and
![]() $d\theta = \eta = 0$
, which is a contradiction. So
$d\theta = \eta = 0$
, which is a contradiction. So
![]() $(\mathcal {L}-\nu )^J$
is not invertible on closed forms, meaning that
$(\mathcal {L}-\nu )^J$
is not invertible on closed forms, meaning that
![]() $\nu \in \sigma _{r+1,\alpha -1,m-1}$
.
$\nu \in \sigma _{r+1,\alpha -1,m-1}$
.
Let
![]() $\sigma ^{-}$
be the eigenvalues associated to generalized eigenvectors of
$\sigma ^{-}$
be the eigenvalues associated to generalized eigenvectors of
![]() $\Phi ^{-1*}:E^{++}\rightarrow E^{++}$
. Note that when
$\Phi ^{-1*}:E^{++}\rightarrow E^{++}$
. Note that when
![]() $d=1$
, this implies that
$d=1$
, this implies that
![]() $\Sigma _1^- = \sigma ^-$
. The following proposition gives Theorem 1.3.
$\Sigma _1^- = \sigma ^-$
. The following proposition gives Theorem 1.3.
Proposition 4.10. For
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>\Lambda $
, the following hold.
$\alpha>\Lambda $
, the following hold.
-
(i) If
 $d=1$
, then the set of eigenvalues for
$d=1$
, then the set of eigenvalues for
 $\mathcal {L}$
acting on
$\mathcal {L}$
acting on
 $\mathcal {B}_0^{r,\alpha }$
contains
$\mathcal {B}_0^{r,\alpha }$
contains
 $\sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
. In addition, if
$\sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
. In addition, if
 $\nu $
is an eigenvalue in
$\nu $
is an eigenvalue in
 $\mathcal {B}_0^{r,\alpha }$
and
$\mathcal {B}_0^{r,\alpha }$
and
 $k<\alpha -\Lambda $
, then
$k<\alpha -\Lambda $
, then
 $\unicode{x3bb} ^{-1}\nu $
is an eigenvalue in
$\unicode{x3bb} ^{-1}\nu $
is an eigenvalue in
 $\mathcal {B}_0^{r+k,\alpha -k}$
. It follows that if
$\mathcal {B}_0^{r+k,\alpha -k}$
. It follows that if
 $\mathcal {F}:= \bigcap _{\alpha>0,r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
$\mathcal {F}:= \bigcap _{\alpha>0,r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
 $\mathcal {F}$
contains the set of numbers of the form
$\mathcal {F}$
contains the set of numbers of the form
 $\unicode{x3bb} ^{-k}\nu $
with
$\unicode{x3bb} ^{-k}\nu $
with
 $\nu \in \sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
and
$\nu \in \sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
and
 $k\in \mathbb {N}$
;
$k\in \mathbb {N}$
; -
(ii) If
 $d=2$
, then the set of eigenvalues for
$d=2$
, then the set of eigenvalues for
 $\mathcal {L}$
acting on
$\mathcal {L}$
acting on
 $\mathcal {B}_0^{r,\alpha }$
contains
$\mathcal {B}_0^{r,\alpha }$
contains
 $\sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
. If
$\sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
. If
 $\mathcal {S}^{\infty }_{\alpha }:= \bigcap _{r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
$\mathcal {S}^{\infty }_{\alpha }:= \bigcap _{r>0}\mathcal {S}^r_{\alpha }$
, then the Ruelle spectrum for functions in
 $\mathcal {S}^{\infty }_{\alpha }$
contains the set
$\mathcal {S}^{\infty }_{\alpha }$
contains the set
 $\sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
.
$\sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}$
.
Proof. Both of these are consequences of Lemma 4.9. For
![]() $d=1$
, that
$d=1$
, that
![]() $\Sigma _1^-\setminus \{\unicode{x3bb} ^{-1}\}$
follows directly from part (iii) of Lemma 4.9. Now suppose that
$\Sigma _1^-\setminus \{\unicode{x3bb} ^{-1}\}$
follows directly from part (iii) of Lemma 4.9. Now suppose that
![]() $\nu \in \sigma _{r,\alpha ,0}$
for some
$\nu \in \sigma _{r,\alpha ,0}$
for some
![]() $|\nu |<1$
. Then by part (i),
$|\nu |<1$
. Then by part (i),
![]() $\unicode{x3bb} ^{-1}\nu \in \sigma _{r,\alpha , 1}$
. So
$\unicode{x3bb} ^{-1}\nu \in \sigma _{r,\alpha , 1}$
. So
![]() $(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\eta = 0$
for some
$(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\eta = 0$
for some
![]() $\eta \in \mathcal {B}_1^{r,\alpha }$
. Since
$\eta \in \mathcal {B}_1^{r,\alpha }$
. Since
![]() $\unicode{x3bb} ^{-1}|\nu |< \unicode{x3bb} ^{-1}$
,
$\unicode{x3bb} ^{-1}|\nu |< \unicode{x3bb} ^{-1}$
,
![]() $\eta $
has to be exact as
$\eta $
has to be exact as
![]() $\Sigma _1^-$
is bounded from below by
$\Sigma _1^-$
is bounded from below by
![]() $\unicode{x3bb} ^{-1}$
. So
$\unicode{x3bb} ^{-1}$
. So
![]() $\eta = d\theta _1$
(where
$\eta = d\theta _1$
(where
![]() $\theta _1\in \mathcal {B}_0^{r+1,\alpha -1}$
is uniquely defined up to a closed
$\theta _1\in \mathcal {B}_0^{r+1,\alpha -1}$
is uniquely defined up to a closed
![]() $0$
-form, that is, a constant) and
$0$
-form, that is, a constant) and
![]() $(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\eta = (\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}d\theta _1 = d(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1 =0$
. Thus, either
$(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\eta = (\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}d\theta _1 = d(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1 =0$
. Thus, either
![]() $(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1$
is closed or
$(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1$
is closed or
![]() $(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1=0$
. If
$(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1=0$
. If
![]() $(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1$
is closed, then it is constant, and denote by
$(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1$
is closed, then it is constant, and denote by
![]() $c_1:= (\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1$
. Letting
$c_1:= (\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1$
. Letting
![]() $\theta _1^{\prime } = \theta _1 - c_1$
, it follows that
$\theta _1^{\prime } = \theta _1 - c_1$
, it follows that
![]() $(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1^{\prime } = 0$
and thus it follows that
$(\mathcal {L}-\unicode{x3bb} ^{-1}\nu )^{J_1}\theta _1^{\prime } = 0$
and thus it follows that
![]() $\unicode{x3bb} ^{-1}\nu \in \sigma _{r+1,\alpha -1,0}$
. So we are back where we started and the same argument gives that
$\unicode{x3bb} ^{-1}\nu \in \sigma _{r+1,\alpha -1,0}$
. So we are back where we started and the same argument gives that
![]() $\unicode{x3bb} ^{-2}\nu \in \sigma _{r+2,\alpha -2,0}$
and so on.
$\unicode{x3bb} ^{-2}\nu \in \sigma _{r+2,\alpha -2,0}$
and so on.
If
![]() $d=2$
, by parts (ii), (iv), and (v) of Lemma 4.9, it follows that
$d=2$
, by parts (ii), (iv), and (v) of Lemma 4.9, it follows that
Let
![]() $\nu \in \sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}\subset \Sigma _2^-\setminus \{\unicode{x3bb} ^{-1}\}$
. First,
$\nu \in \sigma ^-\setminus \{\unicode{x3bb} ^{-1}\}\subset \Sigma _2^-\setminus \{\unicode{x3bb} ^{-1}\}$
. First,
![]() $\nu \not \in \Sigma ^-_1$
, since by definition,
$\nu \not \in \Sigma ^-_1$
, since by definition,
![]() $\nu $
contracts faster than the smallest contracting eigenvalue in
$\nu $
contracts faster than the smallest contracting eigenvalue in
![]() $\Sigma _1^-$
. Now,
$\Sigma _1^-$
. Now,
![]() $\unicode{x3bb} |\nu |>1$
, so by part (ii),
$\unicode{x3bb} |\nu |>1$
, so by part (ii),
![]() $\nu \not \in \sigma _{r-1,\alpha +1,2} = \unicode{x3bb} ^{-1}\sigma _{r-1,\alpha +1,0}$
. So it follows that
$\nu \not \in \sigma _{r-1,\alpha +1,2} = \unicode{x3bb} ^{-1}\sigma _{r-1,\alpha +1,0}$
. So it follows that
![]() $\nu \in \sigma _{r-1,\alpha +1,0}$
.
$\nu \in \sigma _{r-1,\alpha +1,0}$
.
5. Applications to primitive substitution subshifts
Let
![]() $\mathcal {A}$
be a finite set (the alphabet) and
$\mathcal {A}$
be a finite set (the alphabet) and
![]() $\mathcal {A}^{*}$
be the set of finite words on
$\mathcal {A}^{*}$
be the set of finite words on
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\varrho :\mathcal {A}\rightarrow \mathcal {A}^{*}$
be a primitive substitution rule. This means there is an N such that for any
$\varrho :\mathcal {A}\rightarrow \mathcal {A}^{*}$
be a primitive substitution rule. This means there is an N such that for any
![]() $a,b\in \mathcal {A}$
, the symbol a appears in
$a,b\in \mathcal {A}$
, the symbol a appears in
![]() $\varrho ^N(b)$
. Without loss of generality (that is, by passing to a power), we will assume that there is a symbol
$\varrho ^N(b)$
. Without loss of generality (that is, by passing to a power), we will assume that there is a symbol
![]() $a\in \mathcal {A}$
such that
$a\in \mathcal {A}$
such that
![]() $\varrho (a)$
begins with a. Let
$\varrho (a)$
begins with a. Let
![]() $\bar {a} = \lim _{N\rightarrow \infty }\varrho ^N(a) \in \mathcal {A}^{\mathbb {N}}$
be a fixed point of the substitution and define
$\bar {a} = \lim _{N\rightarrow \infty }\varrho ^N(a) \in \mathcal {A}^{\mathbb {N}}$
be a fixed point of the substitution and define
![]() $X_{\varrho }$
to be the orbit closure of
$X_{\varrho }$
to be the orbit closure of
![]() $\bar {a}$
under the shift map
$\bar {a}$
under the shift map
![]() $\sigma :\mathcal {A}^{\mathbb {N}}\rightarrow \mathcal {A}^{\mathbb {N}}$
. The system
$\sigma :\mathcal {A}^{\mathbb {N}}\rightarrow \mathcal {A}^{\mathbb {N}}$
. The system
![]() $\sigma :X_{\varrho }\rightarrow X_{\varrho }$
is a minimal subshift.
$\sigma :X_{\varrho }\rightarrow X_{\varrho }$
is a minimal subshift.
Define the metric on
![]() $X_{\varrho }$
as
$X_{\varrho }$
as
for
![]() $\bar {b},\bar {c}\in X_{\varrho }$
, where
$\bar {b},\bar {c}\in X_{\varrho }$
, where
![]() $k(\bar {b},\bar {c})\in \mathbb {N}$
is the smallest index i so that
$k(\bar {b},\bar {c})\in \mathbb {N}$
is the smallest index i so that
![]() $c_i\neq b_i$
, and
$c_i\neq b_i$
, and
![]() $\unicode{x3bb}>0$
is the Perron–Frobenius eigenvalue of the substitution matrix for
$\unicode{x3bb}>0$
is the Perron–Frobenius eigenvalue of the substitution matrix for
![]() $\varrho $
.
$\varrho $
.
There is an associated solenoid to
![]() $\varrho $
constructed as follows. Let
$\varrho $
constructed as follows. Let
![]() $r:X_{\varrho }\rightarrow \mathbb {R}^+$
be the function defined as
$r:X_{\varrho }\rightarrow \mathbb {R}^+$
be the function defined as
![]() $r(\bar {l}) = v_{l_1}$
, where
$r(\bar {l}) = v_{l_1}$
, where
![]() $v\in \mathbb {R}^{|\mathcal {A}|}$
is a positive Perron–Frobenius eigenvector for the substitution matrix, and let
$v\in \mathbb {R}^{|\mathcal {A}|}$
is a positive Perron–Frobenius eigenvector for the substitution matrix, and let
![]() $\Omega _{\varrho }$
be the suspension of
$\Omega _{\varrho }$
be the suspension of
![]() $X_{\varrho }$
with roof function r. Then there exists a compact one-dimensional CW complex
$X_{\varrho }$
with roof function r. Then there exists a compact one-dimensional CW complex
![]() $\Gamma $
and a cellular affine (outside the zero-cells of
$\Gamma $
and a cellular affine (outside the zero-cells of
![]() $\Gamma $
) map
$\Gamma $
) map
![]() $\gamma :\Gamma \rightarrow \Gamma $
such that
$\gamma :\Gamma \rightarrow \Gamma $
such that
This is the Anderson–Putnam construction [Reference Anderson and PutnamAP98] and the CW complex
![]() $\Gamma $
is referred to as the AP-complex. Denote
$\Gamma $
is referred to as the AP-complex. Denote
![]() $\Gamma _k = \pi _k(\Omega _{\varrho })$
the ‘
$\Gamma _k = \pi _k(\Omega _{\varrho })$
the ‘
![]() $k\mathrm {th}$
’ AP complex. The identification above is not only through a homeomorphism, but in fact an isometry. That is, there is a natural inclusion
$k\mathrm {th}$
’ AP complex. The identification above is not only through a homeomorphism, but in fact an isometry. That is, there is a natural inclusion
![]() $i:X_{\varrho }\rightarrow \Omega _{\varrho }$
which, under the identification above, can be identified with
$i:X_{\varrho }\rightarrow \Omega _{\varrho }$
which, under the identification above, can be identified with
![]() $C^{\perp }_0(\bar {a})$
. This inclusion is an isometry with respect to the metrics in equations (3) and (32). Denote by
$C^{\perp }_0(\bar {a})$
. This inclusion is an isometry with respect to the metrics in equations (3) and (32). Denote by
![]() $H_{\alpha }(X_{\varrho })$
the space of
$H_{\alpha }(X_{\varrho })$
the space of
![]() $\alpha $
-Hölder functions on
$\alpha $
-Hölder functions on
![]() $X_{\varrho }$
with respect to this metric.
$X_{\varrho }$
with respect to this metric.
Let
![]() $0<\varepsilon < \min _{l\in \mathcal {A}} |v_l| /4$
. With this choice of
$0<\varepsilon < \min _{l\in \mathcal {A}} |v_l| /4$
. With this choice of
![]() $\varepsilon $
, the
$\varepsilon $
, the
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $i(X_{\varrho }) = C^{\perp }_0(\bar {a})$
has the local coordinates
$i(X_{\varrho }) = C^{\perp }_0(\bar {a})$
has the local coordinates
![]() $(t,c)\in (-\varepsilon ,\varepsilon )\times X_{\varrho }$
. If
$(t,c)\in (-\varepsilon ,\varepsilon )\times X_{\varrho }$
. If
![]() $u_{\varepsilon }:(-\varepsilon ,\varepsilon )\rightarrow \mathbb {R}$
is a smooth even bump function with compact support and of integral 1, then for any function
$u_{\varepsilon }:(-\varepsilon ,\varepsilon )\rightarrow \mathbb {R}$
is a smooth even bump function with compact support and of integral 1, then for any function
![]() $h:X_{\varrho }\rightarrow \mathbb {R}$
, let
$h:X_{\varrho }\rightarrow \mathbb {R}$
, let
![]() $h_{\varepsilon }:\Omega _{\varrho }\rightarrow \mathbb {R}$
be defined as
$h_{\varepsilon }:\Omega _{\varrho }\rightarrow \mathbb {R}$
be defined as
![]() $h_{\varepsilon }(t,c) = u_{\varepsilon }(t) h(c)$
for
$h_{\varepsilon }(t,c) = u_{\varepsilon }(t) h(c)$
for
![]() $(t,c)\in (-\varepsilon ,\varepsilon )\times X_{\varrho }$
and zero otherwise.
$(t,c)\in (-\varepsilon ,\varepsilon )\times X_{\varrho }$
and zero otherwise.
5.1. The cohomological equation for primitive substitution subshifts
This section is dedicated to the proof of Theorem 1.5 on the solutions of the cohomological equation for primitive substitution subshifts
![]() $\sigma :X_{\varrho }\rightarrow X_{\varrho }$
. That is, the goal here is to find a solution u to the equation
$\sigma :X_{\varrho }\rightarrow X_{\varrho }$
. That is, the goal here is to find a solution u to the equation
![]() $f = u\circ \sigma - u$
for a given f.
$f = u\circ \sigma - u$
for a given f.
Lemma 5.1. If
![]() $h:X_{\varrho }\rightarrow \mathbb {R}$
is
$h:X_{\varrho }\rightarrow \mathbb {R}$
is
![]() $\alpha $
-Hölder, then
$\alpha $
-Hölder, then
![]() $h_{\varepsilon } \in \mathcal {S}^1_{\alpha -1}$
for
$h_{\varepsilon } \in \mathcal {S}^1_{\alpha -1}$
for
![]() $\alpha>1$
. If
$\alpha>1$
. If
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha>2$
, then the cohomology class
$\alpha>2$
, then the cohomology class
![]() $[\star h_{\varepsilon }]\in H^1_{r,\alpha }(\Omega _{\varrho })$
is independent of
$[\star h_{\varepsilon }]\in H^1_{r,\alpha }(\Omega _{\varrho })$
is independent of
![]() $u_{\varepsilon }$
.
$u_{\varepsilon }$
.
Proof. The goal is to write
in the canonical way described in §2.1 with the appropriate bounds on
![]() $\|g_k\|_{C^1(\Gamma _k)}$
. Using the notation of equation (23), define
$\|g_k\|_{C^1(\Gamma _k)}$
. Using the notation of equation (23), define
![]() $h^k_{\varepsilon } := \Pi _kh_{\varepsilon }$
which, in the natural coordinates of the
$h^k_{\varepsilon } := \Pi _kh_{\varepsilon }$
which, in the natural coordinates of the
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $C^{\perp }_0(\bar {a})$
, is defined as
$C^{\perp }_0(\bar {a})$
, is defined as
 $$ \begin{align*}h^k_{\varepsilon}(t,c) = \hat{\nu}_{k,(t,c)}^{-1}\int_{C^{\perp}_k(t,c)}h_{\varepsilon}(t,w)\, d\nu_{k,(t,c)} = u_{\varepsilon}(t)\hat{\nu}_{k,(t,c)}^{-1}\int_{C^{\perp}_k(c)}h(w)\, d\nu_{k,c}.\end{align*} $$
$$ \begin{align*}h^k_{\varepsilon}(t,c) = \hat{\nu}_{k,(t,c)}^{-1}\int_{C^{\perp}_k(t,c)}h_{\varepsilon}(t,w)\, d\nu_{k,(t,c)} = u_{\varepsilon}(t)\hat{\nu}_{k,(t,c)}^{-1}\int_{C^{\perp}_k(c)}h(w)\, d\nu_{k,c}.\end{align*} $$
By the same calculation as in §4.1,
![]() $\|h^k_{\varepsilon } - h_{\varepsilon }\|_{C^0}\leq C_\mu \|u\|_\infty \unicode{x3bb} ^{-\alpha k}$
. Now, letting
$\|h^k_{\varepsilon } - h_{\varepsilon }\|_{C^0}\leq C_\mu \|u\|_\infty \unicode{x3bb} ^{-\alpha k}$
. Now, letting
![]() $h^{-1}_{\varepsilon } = 0$
, for any
$h^{-1}_{\varepsilon } = 0$
, for any
![]() $k\geq 0$
, define
$k\geq 0$
, define
![]() $\delta _k h_{\varepsilon } = h^k_{\varepsilon } - h^{k-1}_{\varepsilon }$
. As such,
$\delta _k h_{\varepsilon } = h^k_{\varepsilon } - h^{k-1}_{\varepsilon }$
. As such,
 $$ \begin{align*}\sum_{j=0}^k \delta_jh_{\varepsilon} = h^k_{\varepsilon}\end{align*} $$
$$ \begin{align*}\sum_{j=0}^k \delta_jh_{\varepsilon} = h^k_{\varepsilon}\end{align*} $$
and, since
![]() $\delta _kh_{\varepsilon }$
only depends on at most the first k coordinates,
$\delta _kh_{\varepsilon }$
only depends on at most the first k coordinates,
![]() $\delta _kh_{\varepsilon } = \pi ^{*}_k g_k$
for some
$\delta _kh_{\varepsilon } = \pi ^{*}_k g_k$
for some
![]() $g_k:\Gamma _k\rightarrow \mathbb {R}$
. If
$g_k:\Gamma _k\rightarrow \mathbb {R}$
. If
![]() $\alpha>1$
, then
$\alpha>1$
, then
![]() $\sum _{j=0}^k \pi ^{*}_kg_k \rightarrow h_{\varepsilon }$
pointwise. It remains to prove the
$\sum _{j=0}^k \pi ^{*}_kg_k \rightarrow h_{\varepsilon }$
pointwise. It remains to prove the
![]() $C^1$
bounds for
$C^1$
bounds for
![]() $g_k$
.
$g_k$
.
Let
![]() $P_k = \gamma ^{-k}(\pi _0(\bar {a}))\subset \Gamma _k$
be the preimages of
$P_k = \gamma ^{-k}(\pi _0(\bar {a}))\subset \Gamma _k$
be the preimages of
![]() $\pi _0(\bar {a})$
under
$\pi _0(\bar {a})$
under
![]() $\gamma ^k$
. These points can be of one of two types: flat points or branch points. Flat points have an Euclidean neighborhood whereas branch points do not.
$\gamma ^k$
. These points can be of one of two types: flat points or branch points. Flat points have an Euclidean neighborhood whereas branch points do not.
Since
![]() $h_{\varepsilon }^k$
is transversally locally constant,
$h_{\varepsilon }^k$
is transversally locally constant,
![]() $h_{\varepsilon }^k = \pi ^{*}_k H_k$
for some
$h_{\varepsilon }^k = \pi ^{*}_k H_k$
for some
![]() $H_k:\Gamma _k\rightarrow \mathbb {R}$
. Note that the task is to obtain
$H_k:\Gamma _k\rightarrow \mathbb {R}$
. Note that the task is to obtain
![]() $C^1$
bounds for
$C^1$
bounds for
![]() $g_k = H_k - \gamma ^{*}H_{k-1}$
.
$g_k = H_k - \gamma ^{*}H_{k-1}$
.
The function
![]() $H_k$
is supported in the
$H_k$
is supported in the
![]() $\unicode{x3bb} ^{-k}\varepsilon $
-neighborhood of
$\unicode{x3bb} ^{-k}\varepsilon $
-neighborhood of
![]() $P_k$
as follows. If
$P_k$
as follows. If
![]() $z\in P_k$
is a flat point, then in the
$z\in P_k$
is a flat point, then in the
![]() $\unicode{x3bb} ^{-k}\varepsilon $
-neighborhood of
$\unicode{x3bb} ^{-k}\varepsilon $
-neighborhood of
![]() $z\in P_k$
, after identifying z with
$z\in P_k$
, after identifying z with
![]() $0$
in these coordinates,
$0$
in these coordinates,
![]() $H_k(t) = u_{\varepsilon }(\unicode{x3bb} ^kt)h^k_{\varepsilon }(c_z)$
, where
$H_k(t) = u_{\varepsilon }(\unicode{x3bb} ^kt)h^k_{\varepsilon }(c_z)$
, where
![]() $c_z\in C^{\perp }_0(\bar {a})$
is a point in the clopen subset of
$c_z\in C^{\perp }_0(\bar {a})$
is a point in the clopen subset of
![]() $X_{\varrho }$
corresponding to z. From this, it follows that in these local coordinates,
$X_{\varrho }$
corresponding to z. From this, it follows that in these local coordinates,
 $$ \begin{align} \begin{aligned} &g_k(t) = u_{\varepsilon}(\unicode{x3bb}^kt)(h^k_{\varepsilon}(c_z) - h^{k-1}_{\varepsilon}(c_z))\\ &\quad=u_{\varepsilon}(\unicode{x3bb}^kt)\bigg[\hat{\nu}_{k,c_z}^{-1}\!\int_{C^{\perp}_k(c_z)} h(w)-h(c_z)\, d\nu_{k,c_z}\! -\! \hat{\nu}_{k-1,c_z}^{-1}\!\int_{C^{\perp}_{k-1}(c_z)} h(w)-h(c_z)\, d\nu_{k,c_z} \bigg] \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &g_k(t) = u_{\varepsilon}(\unicode{x3bb}^kt)(h^k_{\varepsilon}(c_z) - h^{k-1}_{\varepsilon}(c_z))\\ &\quad=u_{\varepsilon}(\unicode{x3bb}^kt)\bigg[\hat{\nu}_{k,c_z}^{-1}\!\int_{C^{\perp}_k(c_z)} h(w)-h(c_z)\, d\nu_{k,c_z}\! -\! \hat{\nu}_{k-1,c_z}^{-1}\!\int_{C^{\perp}_{k-1}(c_z)} h(w)-h(c_z)\, d\nu_{k,c_z} \bigg] \end{aligned} \end{align} $$
in a
![]() $\unicode{x3bb} ^{-k}\varepsilon $
-neighborhood of
$\unicode{x3bb} ^{-k}\varepsilon $
-neighborhood of
![]() $z\in P_k$
. Note that since h is
$z\in P_k$
. Note that since h is
![]() $\alpha $
-Hölder, by rewriting it as in equation (33),
$\alpha $
-Hölder, by rewriting it as in equation (33),
and so
![]() $\|g_k\|_{C^0}\leq 2\unicode{x3bb} C_h\|u_{\varepsilon }\|_\infty \unicode{x3bb} ^{-k\alpha }$
. Moreover, in the neighborhood of
$\|g_k\|_{C^0}\leq 2\unicode{x3bb} C_h\|u_{\varepsilon }\|_\infty \unicode{x3bb} ^{-k\alpha }$
. Moreover, in the neighborhood of
![]() $z\in P_k$
,
$z\in P_k$
,
and so
and so it follows that
![]() $\|g_k\|_{C^1} \leq C \unicode{x3bb} ^{-k(\alpha -1)}$
for all k, and thus
$\|g_k\|_{C^1} \leq C \unicode{x3bb} ^{-k(\alpha -1)}$
for all k, and thus
![]() $h_{\varepsilon } \in \mathcal {S}^1_{\alpha -1}$
. The case of
$h_{\varepsilon } \in \mathcal {S}^1_{\alpha -1}$
. The case of
![]() ${z\in P_k}$
being a branched point is essentially treated in the same way: equation (33) needs to be written carefully to take into consideration the different branches coming out of z. Indeed, equation (33) treats two branches coming out of z in the flat case, and so equation (33) can be used to treat the branched case with minor modifications. The details are left to the reader.
${z\in P_k}$
being a branched point is essentially treated in the same way: equation (33) needs to be written carefully to take into consideration the different branches coming out of z. Indeed, equation (33) treats two branches coming out of z in the flat case, and so equation (33) can be used to treat the branched case with minor modifications. The details are left to the reader.
That the cohomology class is independent of
![]() $u_{\varepsilon }$
follows from the fact that the compactly supported de Rham cohomology of the line is one-dimensional in top degree.
$u_{\varepsilon }$
follows from the fact that the compactly supported de Rham cohomology of the line is one-dimensional in top degree.
Remark 5.2. Note that the same proof can be modified to show that
![]() $h_{\varepsilon }\in \mathcal {S}^r_{\alpha -r}$
for any
$h_{\varepsilon }\in \mathcal {S}^r_{\alpha -r}$
for any
![]() $r<\alpha $
. However, the focus is on
$r<\alpha $
. However, the focus is on
![]() $r=1$
since the transverse Hölder regularity is what needs to be optimized.
$r=1$
since the transverse Hölder regularity is what needs to be optimized.
Definition 5.3.
![]() $f:X_{\varrho }\rightarrow \mathbb {R}$
is a coboundary if there exists an
$f:X_{\varrho }\rightarrow \mathbb {R}$
is a coboundary if there exists an
![]() $f:X_{\varrho }\rightarrow \mathbb {R}$
such that
$f:X_{\varrho }\rightarrow \mathbb {R}$
such that
![]() $f = g\circ \sigma - g$
. For
$f = g\circ \sigma - g$
. For
![]() $\alpha>0$
, it is an
$\alpha>0$
, it is an
![]() $\alpha $
-coboundary if f is
$\alpha $
-coboundary if f is
![]() $\alpha $
-Hölder and g is
$\alpha $
-Hölder and g is
![]() $(\alpha -2)$
-Hölder. The
$(\alpha -2)$
-Hölder. The
![]() $\alpha $
-Hölder cohomology
$\alpha $
-Hölder cohomology
![]() $H_{\alpha }^0(X_{\varrho })$
of
$H_{\alpha }^0(X_{\varrho })$
of
![]() $X_{\varrho }$
is the quotient of
$X_{\varrho }$
is the quotient of
![]() $H_{\alpha }(X_{\varrho })$
by the equivalence relation
$H_{\alpha }(X_{\varrho })$
by the equivalence relation
![]() $f_1\sim f_2$
if and only if
$f_1\sim f_2$
if and only if
![]() $f_1-f_2$
is an
$f_1-f_2$
is an
![]() $\alpha $
-coboundary.
$\alpha $
-coboundary.
In what follows, X is the differential operator in the leaf direction.
Lemma 5.4. For
![]() $\alpha>2$
and an
$\alpha>2$
and an
![]() $\alpha $
-Hölder function h on
$\alpha $
-Hölder function h on
![]() $X_{\varrho }$
,
$X_{\varrho }$
,
![]() $h = g\circ \sigma - g$
for some
$h = g\circ \sigma - g$
for some
![]() $g\in H_{\alpha -2}(X_{\varrho })$
if and only if
$g\in H_{\alpha -2}(X_{\varrho })$
if and only if
![]() $h_{\varepsilon } = X \Theta $
for some
$h_{\varepsilon } = X \Theta $
for some
![]() $\Theta \in \mathcal {S}^2_{\alpha -2}$
.
$\Theta \in \mathcal {S}^2_{\alpha -2}$
.
Proof. Suppose
![]() $h_{\varepsilon } = X \Theta $
. By Lemma 5.1,
$h_{\varepsilon } = X \Theta $
. By Lemma 5.1,
![]() $h_{\varepsilon }\in \mathcal {S}^1_{\alpha -1}$
, and so
$h_{\varepsilon }\in \mathcal {S}^1_{\alpha -1}$
, and so
![]() $\Theta \in \mathcal {S}^2_{\alpha -2}$
by Proposition 2.3. Since
$\Theta \in \mathcal {S}^2_{\alpha -2}$
by Proposition 2.3. Since
![]() $u_{\varepsilon }$
has integral one,
$u_{\varepsilon }$
has integral one,
 $$ \begin{align*}h(c) = \int_{-\varepsilon}^\varepsilon h_{\varepsilon}(t,c)\, dt = \int_{-\varepsilon}^\varepsilon X\Theta(t,c)\, dt = \Theta(\varepsilon,c) - \Theta(-\varepsilon,c).\end{align*} $$
$$ \begin{align*}h(c) = \int_{-\varepsilon}^\varepsilon h_{\varepsilon}(t,c)\, dt = \int_{-\varepsilon}^\varepsilon X\Theta(t,c)\, dt = \Theta(\varepsilon,c) - \Theta(-\varepsilon,c).\end{align*} $$
Now, since
![]() $h_{\varepsilon }$
is compactly supported in the
$h_{\varepsilon }$
is compactly supported in the
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $i(X_{\varrho })$
and
$i(X_{\varrho })$
and
![]() $0 = h_{\varepsilon }(\pm \varepsilon ,c) = X\Theta (\pm \varepsilon ,c)$
,
$0 = h_{\varepsilon }(\pm \varepsilon ,c) = X\Theta (\pm \varepsilon ,c)$
,
![]() $\Theta $
is leafwise constant on the complement of the
$\Theta $
is leafwise constant on the complement of the
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $i(X_{\varrho })$
, which implies that
$i(X_{\varrho })$
, which implies that
![]() $\Theta (\varepsilon ,c) = \Theta (-\varepsilon ,\sigma (c))$
. Defining
$\Theta (\varepsilon ,c) = \Theta (-\varepsilon ,\sigma (c))$
. Defining
![]() $g(c) = \Theta (-\varepsilon ,c)$
, it follows that
$g(c) = \Theta (-\varepsilon ,c)$
, it follows that
![]() $h = g\circ \sigma - g$
.
$h = g\circ \sigma - g$
.
Write
![]() $\Theta = \sum _{k\geq 0} \pi ^{*}_k\Theta _k$
in the canonical way described in §2.1, and, in the local coordinates around
$\Theta = \sum _{k\geq 0} \pi ^{*}_k\Theta _k$
in the canonical way described in §2.1, and, in the local coordinates around
![]() $i(X_{\varrho })$
, let
$i(X_{\varrho })$
, let
![]() $(-\varepsilon ,c_1)\in C_k^{\perp }((-\varepsilon ,c_2))\setminus C_{k+1}^{\perp }((-\varepsilon ,c_2))$
. For
$(-\varepsilon ,c_1)\in C_k^{\perp }((-\varepsilon ,c_2))\setminus C_{k+1}^{\perp }((-\varepsilon ,c_2))$
. For
![]() $\beta>0$
,
$\beta>0$
,
 $$ \begin{align*} \begin{aligned} \frac{|g(c_1)-g(c_2)|}{\unicode{x3bb}^{-\beta k}} &= \unicode{x3bb}^{\beta k}|\Theta(-\varepsilon, c_1) - \Theta(-\varepsilon, c_2)|\! \leq \unicode{x3bb}^{\beta k}\!\sum_{n\geq k} |\pi^{*}_n\Theta_n (-\varepsilon, c_1) -\! \pi^{*}_n\Theta_n (-\varepsilon, c_2)| \\ &\leq \unicode{x3bb}^{\beta n} \sum_{n\geq k} \|\Theta_n\|_{C^2}\leq \unicode{x3bb}^{\beta k} C_\Theta \frac{\unicode{x3bb}^{-k(\alpha-2)}}{1-\unicode{x3bb}^{-(\alpha-2)}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{|g(c_1)-g(c_2)|}{\unicode{x3bb}^{-\beta k}} &= \unicode{x3bb}^{\beta k}|\Theta(-\varepsilon, c_1) - \Theta(-\varepsilon, c_2)|\! \leq \unicode{x3bb}^{\beta k}\!\sum_{n\geq k} |\pi^{*}_n\Theta_n (-\varepsilon, c_1) -\! \pi^{*}_n\Theta_n (-\varepsilon, c_2)| \\ &\leq \unicode{x3bb}^{\beta n} \sum_{n\geq k} \|\Theta_n\|_{C^2}\leq \unicode{x3bb}^{\beta k} C_\Theta \frac{\unicode{x3bb}^{-k(\alpha-2)}}{1-\unicode{x3bb}^{-(\alpha-2)}}. \end{aligned} \end{align*} $$
Picking
![]() $\beta = \alpha -2$
, it follows that g has finite
$\beta = \alpha -2$
, it follows that g has finite
![]() $\alpha -2$
Hölder norm, and so
$\alpha -2$
Hölder norm, and so
![]() $g\in H_{\alpha -2}(X_{\varrho })$
.
$g\in H_{\alpha -2}(X_{\varrho })$
.
Now suppose
![]() $h = g\circ \sigma - g$
and consider
$h = g\circ \sigma - g$
and consider
![]() $h_{\varepsilon }$
as constructed above. In the
$h_{\varepsilon }$
as constructed above. In the
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $i(X_{\varrho })$
, define
$i(X_{\varrho })$
, define
![]() $\Theta (t,c) = g(c)+\int _{-\varepsilon }^t u_{\varepsilon }(s)h(c)\,ds $
and so close to
$\Theta (t,c) = g(c)+\int _{-\varepsilon }^t u_{\varepsilon }(s)h(c)\,ds $
and so close to
![]() $i(X_{\varrho })$
, it holds that
$i(X_{\varrho })$
, it holds that
![]() $X\Theta = h_{\varepsilon }$
. By construction, and by the fact that
$X\Theta = h_{\varepsilon }$
. By construction, and by the fact that
![]() $h = g\circ \sigma - g$
, this function satisfies
$h = g\circ \sigma - g$
, this function satisfies
![]() $h_{\varepsilon } = X\Theta $
globally. The details are left to the reader.
$h_{\varepsilon } = X\Theta $
globally. The details are left to the reader.
Lemmas 5.1 and 5.4 imply that the induced map
![]() $j:H_{\alpha }^0(X_{\varrho })\rightarrow H^1_{1,\alpha -1}(\Omega _{\varrho })\cong \check H^1(\Omega _{\varrho };\mathbb {R})$
defined by
$j:H_{\alpha }^0(X_{\varrho })\rightarrow H^1_{1,\alpha -1}(\Omega _{\varrho })\cong \check H^1(\Omega _{\varrho };\mathbb {R})$
defined by
![]() $j([f]) = [\star f_{\varepsilon }]$
is injective whenever
$j([f]) = [\star f_{\varepsilon }]$
is injective whenever
![]() $\alpha>2$
. This implies that
$\alpha>2$
. This implies that
![]() $H^0_{\alpha }(X_{\varrho })$
is finite dimensional and concludes the proof of Theorem 1.5.
$H^0_{\alpha }(X_{\varrho })$
is finite dimensional and concludes the proof of Theorem 1.5.
Acknowledgements
I am indebted to Daniele Galli, Scott Schmieding, Giovanni Forni, and Oliver Butterley for very useful discussions during the preparation of this paper. This work was partially supported by grant 712227 of the Simons Foundation, as well as DMS grant 2143133 from the National Science Foundation.