Introduction
Physical understanding of crack propagation plays an essential role in the industry, and mechanical properties of materials with cracks have been studied for a wide range of materials such as metal, glass, and polymer. Recently, polymer materials attract considerable attention as a low-weight, tough, and inexpensive material for a new era. For example, recent polymer science has provided high toughness,[1] self-healing properties,[Reference Phadke, Zhang, Arman, Hsu, Mashelkar, Lele, Tauber, Arya and Varghese2] and high stretchablility[Reference Haraguchi and Takehisa3, Reference Imran, Esaki, Gotoh, Seki, Ito, Sakai and Takeoka4] with polymer materials. The polymer is a promising material, but an understanding of its fracture mechanism is still a challenging issue partially because both of its visco-elastic property and molecular-network structure are complex.
In the literature, crack behavior in polymer sheets has been studied with various methods, which include tensile,[Reference Lake and Lindley5, Reference Lake and Lindley6] trouser,[Reference Thomas7] cutting,[Reference Lake and Yeoh8] tearing,[Reference Rivlin and Thomas9] and fixed-grip methods.[Reference Tsunoda, Busfield, Davies and Thomas10] Most of the previous studies conclude that the energy for tearing a polymer sheet correlates with the propagation velocity of a crack. Among these experimental methods, the fixed-grip method is a unique method to explore the behavior of crack propagation in polymer sheets. With this method, the so-called energy release rate G, which corresponds to tearing energy, takes a constant value during crack propagation, and the relationship between the energy release rate G and the crack-propagation velocity V can be clearly quantified. With the fixed-grip method, interesting characteristics of crack propagation on rubber sheets have been found: (1) power laws between energy release rate and crack velocity, and (2) a drastic velocity jump from a slow mode (~1 mm/s) to a fast mode (~1000 mm/s) at a critical release rate.[Reference Tsunoda, Busfield, Davies and Thomas10] The crack propagation under the fixed-grip condition has also been studied using the finite-element method, and the numerical results are qualitatively in accordance with experimental results.[Reference Kubo and Umeno11] More recently, an analytical theory reproduces the velocity jump, clarifying the physics of the jump.[Reference Sakumichi and Okumura12] Conventionally, the crack propagation in polymer sheets has been studied mainly based on their visco-elastic properties. Considering characteristic times[Reference Saulnier, Ondarçuhu, Aradian and Raphaël13] or rheological data,[Reference Persson and Brener14, Reference Morishita, Tsunoda and Urayama15] forms of crack tips and crack velocities are explained. On the contrary, recent works claim that crack mechanism is also affected by the size of internal structures in polymer sheets. For example, by tuning a molecular weight of a cross-linking point of styrene-butadiene rubber, the relation between energy release rate versus tear rate is changed.[Reference Tsunoda, Busfield, Davies and Thomas10] In the case of a polyethylene foam sheet whose typical foam size is of millimeter-scale, it was found that the flow of polymer happens only on the scale of foam at the crack tip.[Reference Kashima and Okumura16] The structural size-effect is also verified with numerical simulations; it has been shown that, by changing the mesh size of a network model for elastic sheets, the failure stress of a sheet with a crack can be tuned.[Reference Murano and Okumura17] For crack propagation, in a numerical simulation[Reference Aoyanagi and Okumura18] and a theoretical model,[Reference Sakumichi and Okumura12] it is confirmed that mesh size affects crack velocities. In summary, recent works have implied that certain structural sizes of polymer sheets such as foam size and distance between cross-linking points, which correspond to the mesh size in theory and simulations, affect crack propagation and strength.
The importance of structural sizes in fracture of materials is not limited for polymer science. In Nature, biological soft/hard composites exhibit mechanical toughness (e.g., bones,[Reference Fratzl, Gupta, Paschalis and Roschger19, Reference Hellmich, Barthélémy and Dormieux20] nacre,[Reference Sarikaya, Liu and Aksay21] the exoskeleton of crustaceans[Reference Nikolov, Petrov, Lymperakis, Friák, Sachs, Fabritius, Raabe and Neugebauer22, Reference Sachs, Fabritius and Raabe23]). Especially, soft bones of sea cucumbers,[Reference Emlet24] the skeleton of a certain sponge,[Reference Aizenberg, Weaver, Thanawala, Sundar, Morse and Fratzl25] and the frustule of diatoms[Reference Hamm, Merkel, Springer, Jurkojc, Maier, Prechtel and Smetacek26] have void/material structures and can be regarded as ultimate soft/hard composites, in which voids play a role of soft elements. Accordingly, findings on crack propagation in porous media, which have void/material structures, help us to understand soft/hard composites in Nature and contribute to the development of bio-inspired tough materials.
In this work, we change explicitly the representative scale of structural size and study its effect on the relationship between energy release rate and crack-propagation velocity by using three types of porous polymer sheets: two polymer foam sheets (PFSs) and a nano-porous polymer sheet (NPS). All of the three sheets have similar visco-elastic properties, but the different crack behavior is observed in the experiment. Power laws between crack velocity and energy release rate are found for the two PFSs, while, for the NPS, crack propagation occurs only above a threshold value for energy release rate and the propagation velocity depends on energy release rate only weakly. Furthermore, our results share a common feature with previous experimental results obtained from rubber sheets, in terms of the size of internal structures. As a characteristic structural size (foam size and the distance between cross-linking point) increases, the exponent s of the power law between the energy release rate G and the crack velocity V (G ~ Vs) increases. We present below experimental results and their physical interpretation.
Experiment
Materials
In this experiment, we used three types of porous polymer sheets (PFS1, PFS2, and NPS), which have different foam sizes or pore sizes. The pore sizes of PFS1 and PFS2 are ~0.5 and ~0.2 mm, respectively, and the pore size of NPS is ~100 nm. Thicknesses of PFS1, PFS2, and NPS are 1, 2 mm, and 20 µm, respectively. The PFSs are commercially available from Sekisui Chemical Co. Ltd. (PFS1: Lightron and PFS2: Softron). Figures 1(a)–1(c) show SEM images of the polymer sheets used for experiments. Their visco-elastic properties were measured by using rheometers (Anton Paar: MCR302 for PFS, and ITK: DVA-200 for NPS) as specified in Figs. 1(d)–1(f). Samples for visco-elastic measurements were prepared in the following manner. First, porous polymer sheets were cut into strips, and both the ends of a strip were fixed to jigs. To avoid the slackening of the strip, the strip was slightly stretched by applying a pre-stretching force in the direction of sample length before starting a measurement. By applying a periodic twisting or stretching strain at 1 Hz, visco-elastic properties were measured at different temperatures. Conditions for measurement including sample properties (method, sample size, pre-stretching force, measuring frequency, applied strain, the range of temperature, material and cross-linking) are specified in Table I.
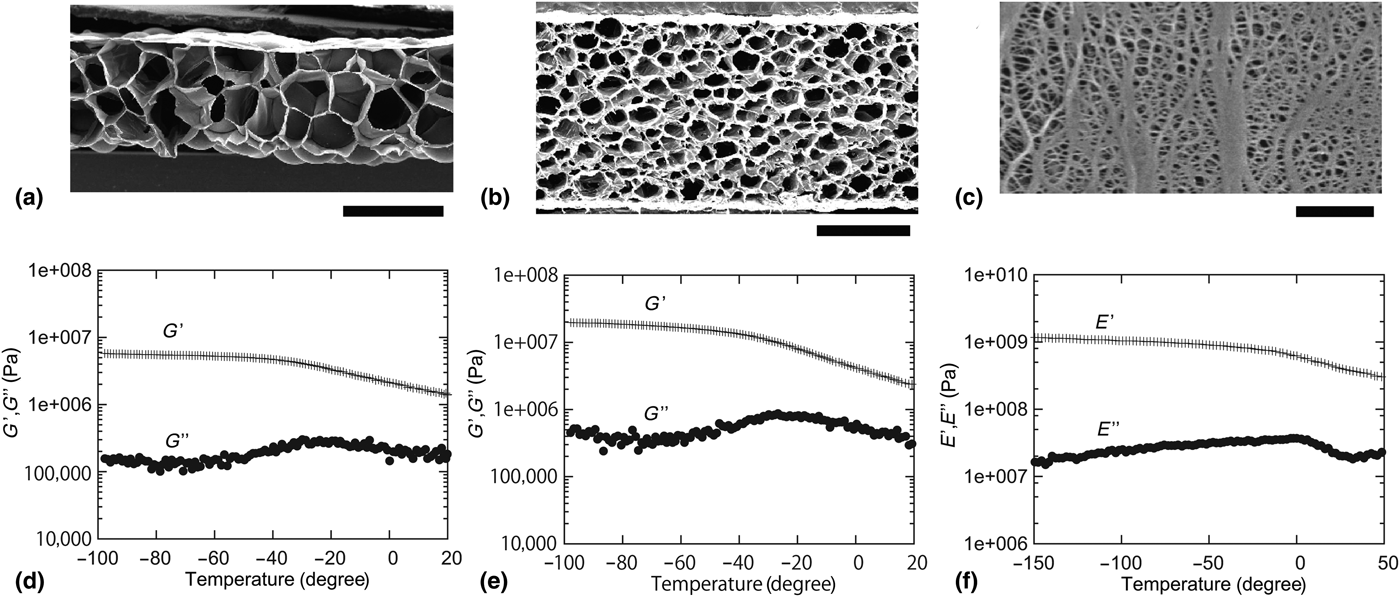
Figure 1. SEM images of polymer sheets. (a) PFS type 1: foam size ~0.5 mm (scale bar: 1 mm) (b) PFS type 2: foam size ~0.2 mm (scale bar: 1 mm) (c) SEM image of NPS (Copyright 2018 by Mitsubishi Chemical Corporation): pore size ~100 nm (scale bar: 1 µm). Twisting storage and loss modulus (G′ and G″) of PFS (d) type 1 and (e) type 2. (f) Stretch storage and loss modulus (E′ and E″) of NPS (Copyright 2018 by Mitsubishi Chemical Corporation).
Table I. Condition of measurement.

In Figs. 1(d)–1(f), by virtue of the time-temperature correspondence principle,[Reference Ferry27] visco-elastic properties in high and low-temperature regions correspond roughly to those in low- and high-frequency regions, respectively. The results for the three samples, two PFSs and a NPS, reflect a typical visco-elastic property of bulk polymer solids. At low temperatures (high frequencies), the polymer sheets are in a glassy state (viscosity is not dominant); at high temperatures (higher than the glass transition temperature), both storage and loss moduli of the polymer sheets tend to decrease. In other words, all three samples possess similar visco-elastic properties. However, as presented later, distinctly different fracture behavior was observed.
Mechanical properties of matrix materials (i.e., cell walls and/or cell frames of each foam or pore in PFS and NPS) are relevant for elucidating crack behavior near the tip. However, in the present samples, the sizes of such matrix materials are minute, which is comparable with the size of a cellular structure; cutting them out from samples and directly performing mechanical measurements on them are practically impossible. For this technical reason, we instead provide in this paper visco-elastic properties of the polymer sheets measured with rheometer by using stripes of dimension larger than the size of matrix materials, considering that it reflects physical properties of the matrix materials. As visco-elastic properties contain characteristics concerning frequency, they are appropriate for discussing crack propagation.
In the present study, we examine a sheet with a porous structure, for which we consider below the pore size is significantly important for considering crack propagation. In porous materials, physical properties such as crystallinity and glass-transition temperature of matrix materials can change with the size of pores. However, the direct measurement for matrix materials is impossible as explained above while these matrix properties are reflected in bulk viscoelastic measurements to some extent, which is similar for the three samples. In addition, the most important length scale at crack tips is the pore size; for example, the crack opening distance, the size of yielding zone near the crack tips,[Reference Chiu, Gent and White28] the size of the region in which viscous flow occurs,[Reference Kashima and Okumura16] and the radius of curvature at a crack tip are all governed by the pore size. These are the reasons we consider the pore size should be physically most important for considering crack propagation in the present porous polymers.
Fixed-grip measurement
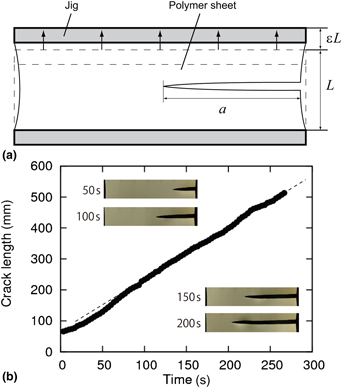
As shown in Fig. 2(a), both ends of a polymer sheet of initial length L is fixed with applying a fixed strain ε. Once introducing an initial crack at one of the two side edges, the elastic energy stored in the polymer sheet starts to be released to initiate crack propagation. Before introducing the initial crack, a stretch is manually applied to the sheet, and the stretch is fixed by a pair of clamping plates. This preparation for giving a pre-stretch before introducing the initial crack is completed within 30 min at room temperature around 25 °C. Figure 2(b) presents the typical experimental result of crack propagation with the fixed-grip geometry (i.e. the relationship between crack length a and time). Except for an initial transient period of crack propagation (t < 50 s), the crack propagates at a constant speed. Here, we study the relationship between the constant crack velocity and the energy release rate for the three samples (PFSs and NPS). In the experiments, the maximum height of the sheet is set L to be either 200, 150, or 100 mm as indicated in the corresponding plots, while the width is set to be at least 2.5 times as large as L. In such a case, we can assume that the shape of a crack tip during crack propagation remains the same and thus energy release rate is constant. This constant can be represented by S ε 2L, where S is the shear modulus of the sheet, for small strains. Note that in the present experiments the maximum strains are relatively small: strains were applied up to ε = 18.5%, ε = 28%, ε = 15% for PFS1, PFS2, and NPS, respectively.
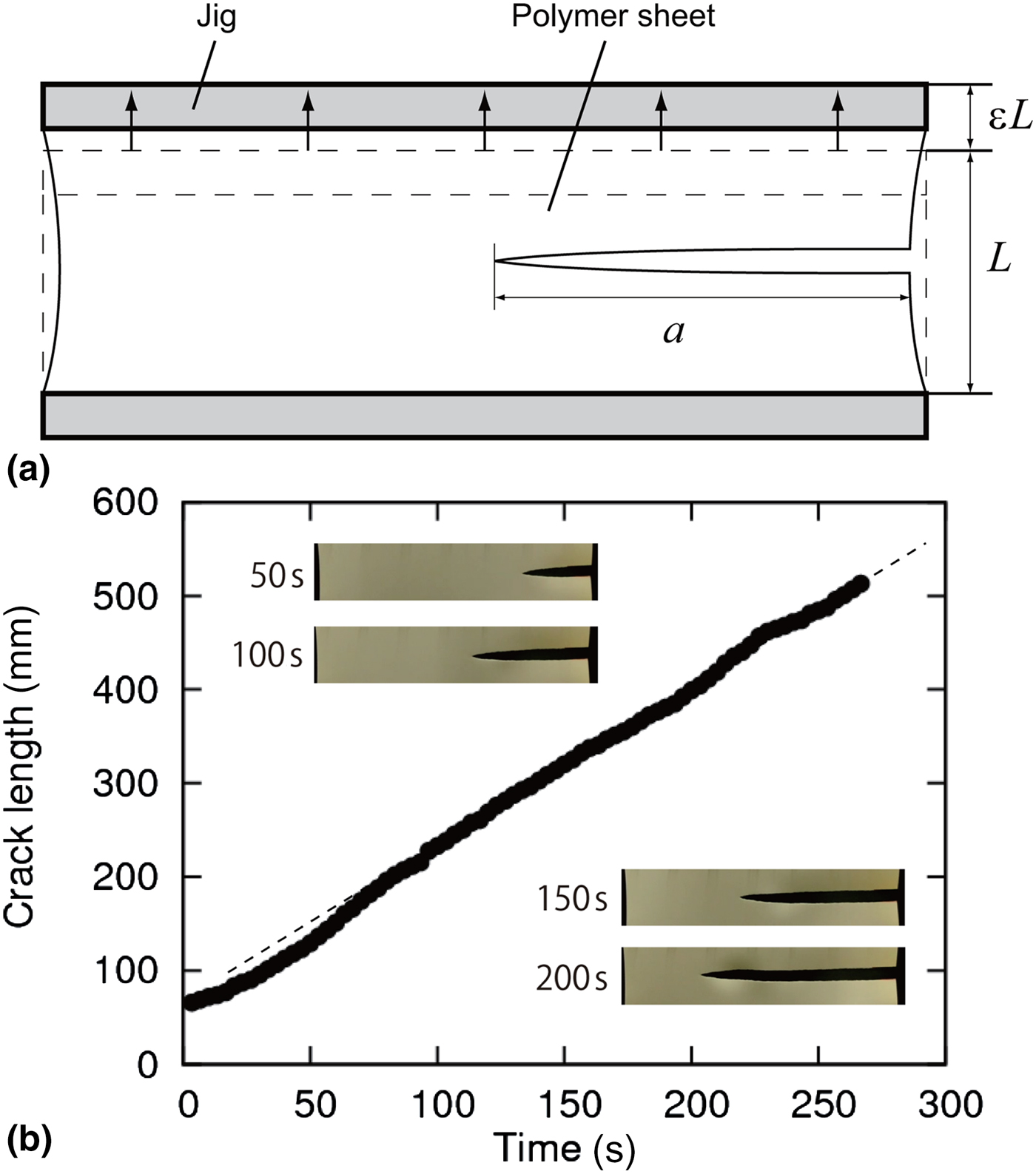
Figure 2. (a) Schematic of the fixed-grip method (b) Relationship between the crack length a and time. Images of crack tips at 50, 100, 150 and 200 s are embedded.
Result
Polymer foam sheet
Figure 3 shows the relationship between ε 2L and V of the two PFSs. In the figure, error bars represent the experimental precision for ε, which is ±1%. For both sheets, the crack velocity increases as ε 2L increases in the range from 0.01 to 10 mm/s. For both PFS1 and PFS2, the power law ε 2L ~ Vs between energy release rate and crack velocity are observed with different values for the exponents s, which are 7 and 5, respectively. For PFS1 and PFS2, the crack did not propagate for ε 2L smaller than 2.2 (ε = 10.5% and L = 200 mm) and 2.88 (ε = 12% and L = 200 mm), respectively. The power law G ~ Vs is also reported for other polymer materials with different exponents (s = 1/2,[Reference Lefranc and Bouchaud29] 1,[Reference Bouchbinder and Brener30, Reference Bhuyan, Tanguy, Martina, Lindner, Ciccotti and Creton31] 3,[Reference Gent32] 4.[Reference Lake and Lindley5] The values s = 7 and 5 obtained in this paper are higher than those reported in the previous works.
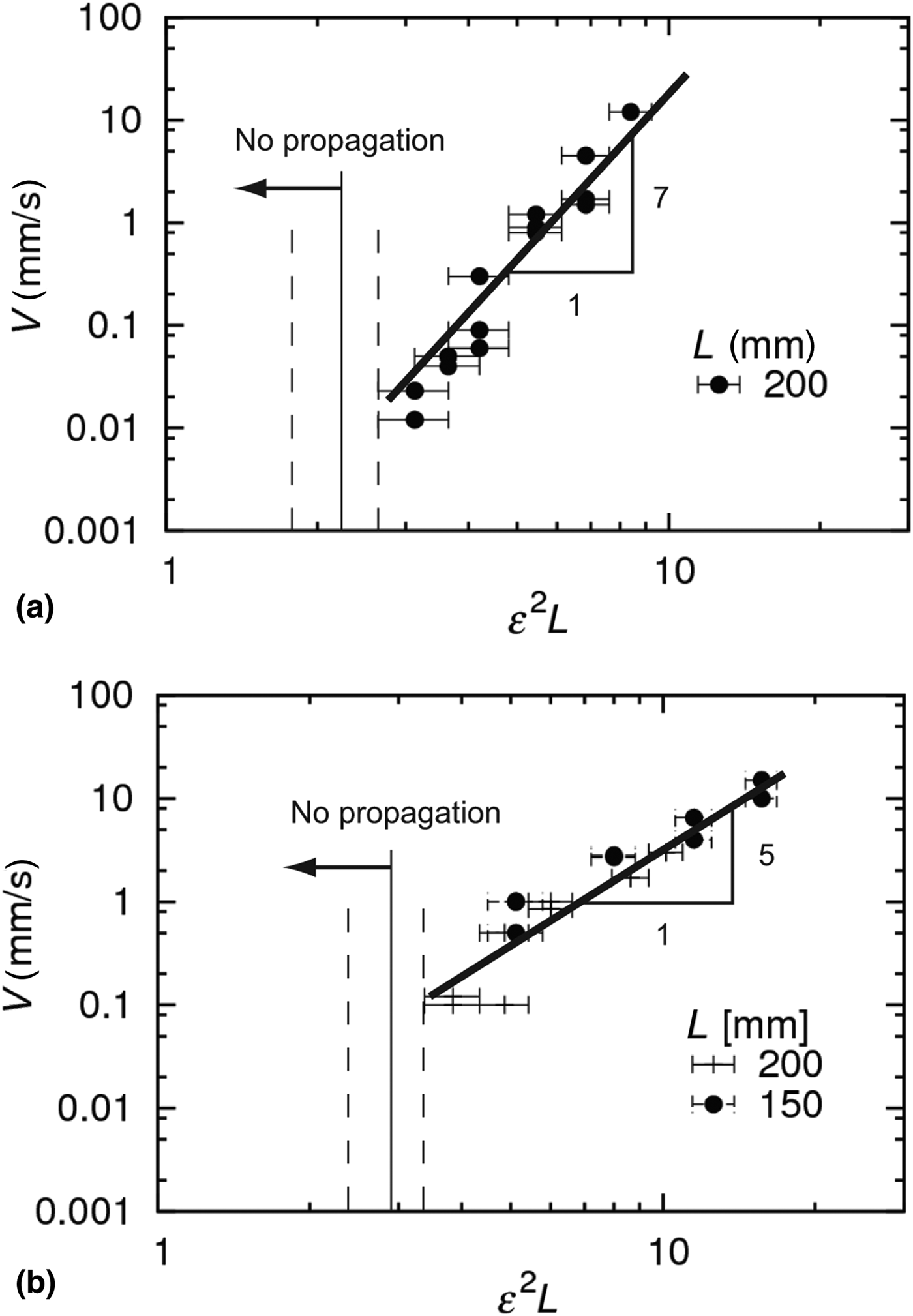
Figure 3. Relationship between the crack velocity V and the measure of energy release rate ε 2L obtained for (a) PFS1 and (b) PFS2. The horizontal axis is given in the unit (mm).
Nano-porous sheet
The relationship between ε 2L and V were also measured for the NPS. As shown in Fig. 4, different from the PFSs, the crack on the NPS was propagated almost at a constant speed ≃5 × 105 mm/s for ε 2L larger than 0.5. As in Fig. 3, we show in Fig. 4 error bars which represent the experimental precision for ε, which is ±1%. Therefore, a clear determination of the velocity dependence on ε 2L around 0.1 was difficult in the present experiment. In Fig. 4, the crack velocity ranges from 1 × 105 to 5 × 105 mm/s, and the range is narrower compared with the two PFSs.
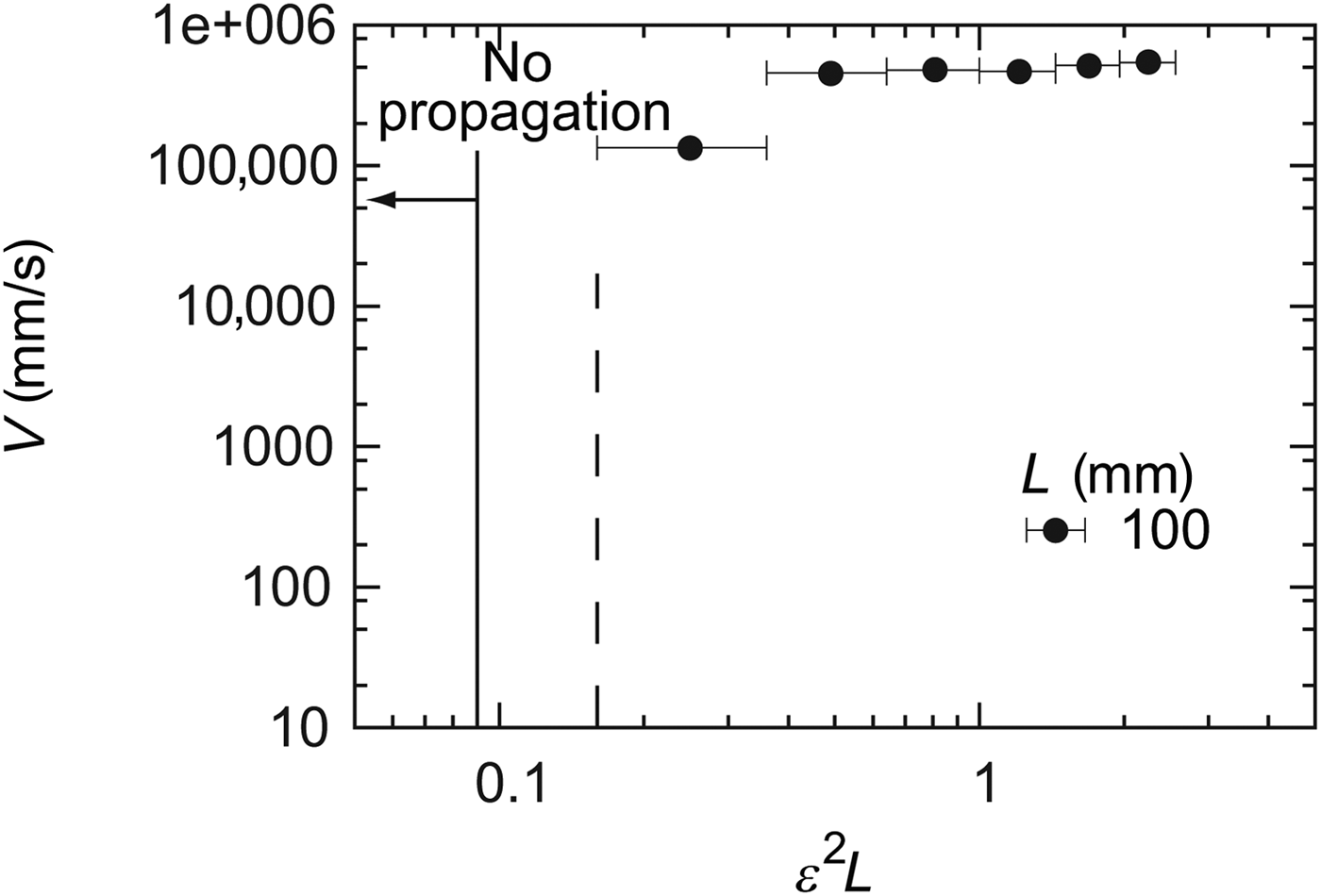
Figure 4. Relationship between the crack velocity V and the measure of energy release rate ε 2L obtained for NPS. The horizontal axis is given in the unit (mm).
Discussion
In this study, we measure the relationship between G and V for the three samples of two PFSs and a NPS under the fixed grip geometry as has been performed for rubber sheets. Although the visco-elastic properties of PFSs and NPS are similar, the G–V relations are different.
To consider the physical origin of the difference, it is helpful to introduce a representative time scale to cut one unit-length concerning the structure of a polymer sheet (foam or pore). By denoting this representative scale by r, a representative time scale can be introduced as r/V. For PFSs and NPS, r is of the order of ~1 and ~100 nm, and V is ~10 and ~1 × 105 mm/s, which means that r/V is 0.1 s and 10−9 s, respectively.
Considering the significant difference in these representative timescales, we can discuss the difference in the G–V relation. Based on the estimation above, for PFSs the visco-elastic property at low frequencies tends to govern the dynamics of crack propagation, i.e., the viscous effect is important. In contrast, for NPS, the visco-elastic property at high frequencies is dominant, i.e., the viscous effect is less important; in the case of NPS, polymer behaves as a glassy material, and crack propagates at a velocity comparable with that for elastic shear wave, which is of the order of the observed velocity around 5 × 105 mm/s.
As for the power law, G~Vs observed in the two PFSs, the exponent s becomes large, as the foam size increases, as shown in Fig. 3. This tendency is in accordance with a tendency that has been observed in rubber sheets. For rubber sheets, the exponent s becomes large, as a molecular weight between two adjacent cross-linking points increases.[Reference Tsunoda, Busfield, Davies and Thomas10] These facts imply that the structure of polymer sheets significantly affects the dynamics of crack propagation.
However, the G–V relations for PFSs and rubber sheets have different features. For example, a velocity jump from a slow mode to a fast mode is clearly observed for rubber sheets,[Reference Tsunoda, Busfield, Davies and Thomas10] which is not observed for PFSs. This difference may be derived from the fact that a visco-elastic property of rubber is more complex than that of polyethylene and polypropylene; the former possesses an extra rubber-like plateau in the rheology data, which is absent in Fig. 1 and is suggested to be indispensable for the velocity jump in Ref. Reference Tsunoda, Busfield, Davies and Thomas10. For rubber sheets, in addition to this complexity in rheological responses, we have to consider the difficulty in determining their representative scale in the structure because not only crosslinks but also fillers forms structures. Therefore, additional study is necessary for further discussion.
Conclusion
We study the impact of structural sizes on the G–V relation. We used two PFSs and a NPS, which possess different representative length scales and observed their crack propagation under the fixed-grip condition. Although all of three polymer sheets have similar visco-elastic properties, different behavior in crack propagation was observed. The difference is considered on the basis of the time scale to cut one structural unit. During crack propagation, visco-elastic properties at low- and high-frequencies are dominant for the PFSs and the NPS, respectively. By examining experimental results in the present study on porous polymer sheets and the previous studies on rubber sheets, the importance of the representative structural length-scale on fracture behavior is revealed. In the literature, crack propagation has been discussed mainly by considering the visco-elastic spectrum. In contrast, in this work, we verify that the representative structural scale of sheets affects the dynamics of crack propagation. This work may also contribute to the understanding of mechanical properties of polymer materials and bio-inspired soft/hard composite materials.
Acknowledgment
The authors are grateful to Sekisui Chemical Co., Ltd. for providing PFSs and Mitsubishi Chemical Corporation for providing nano-porous sheets, the SEM image [Fig. 1(c)], and the viscoelastic plots [Fig. 1(f)]. This work was partly supported by ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan).