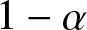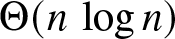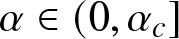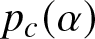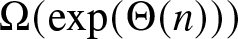1. Introduction
Opinion dynamical models are used extensively in statistical physics and computer science to study the effects of different local interaction rules on the adoption of new technologies and products. One key question in this context is how fast can a new/superior technology replace an old/outdated technology in a network of connected of agents? Classical opinion dynamical models with two competing opinions (or technologies) assume the opinions to be indistinguishable; indeed under both voter and majority rule models, agents update their opinions purely based on the opinions of other agents in their neighborhoods without exhibiting any preference for any opinion. However, to capture the inherent superiority of one opinion over another, we need to incorporate some form of “bias” toward one of the two opinions.
Opinion dynamical models with bias have been studied recently in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1, Reference Lesfari, Giroire and Pérennes17, Reference Mukhopadhyay, Mazumdar and Roy19, Reference Mukhopadhyay, Mazumdar and Roy20]. A strong form of bias is considered in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1, Reference Lesfari, Giroire and Pérennes17]; a bias parameter ![]() $\alpha \in (0,1)$ is introduced; with probability α, an agent is assumed to perform a biased update, in which it adopts the superior opinion independently of its current opinion and opinions of all other agents; with probability
$\alpha \in (0,1)$ is introduced; with probability α, an agent is assumed to perform a biased update, in which it adopts the superior opinion independently of its current opinion and opinions of all other agents; with probability ![]() $1-\alpha$, the agent performs a regular update, in which it adopts the majority opinion among all agents in its neighborhood. The later update rule is often referred to as the majority rule in the literature. Clearly, in this model, any network will eventually reach consensus on the superior opinion. It is shown in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1] that the expected time taken for the network to reach consensus on the superior opinion is exponential in the minimum degree of the underlying graph. Thus, in graphs where the neighborhood size of each agent is proportional to the network size, the consensus time grows exponentially with the network size. This naturally prompts the question if simpler rules exist under which consensus can be achieved faster.
$1-\alpha$, the agent performs a regular update, in which it adopts the majority opinion among all agents in its neighborhood. The later update rule is often referred to as the majority rule in the literature. Clearly, in this model, any network will eventually reach consensus on the superior opinion. It is shown in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1] that the expected time taken for the network to reach consensus on the superior opinion is exponential in the minimum degree of the underlying graph. Thus, in graphs where the neighborhood size of each agent is proportional to the network size, the consensus time grows exponentially with the network size. This naturally prompts the question if simpler rules exist under which consensus can be achieved faster.
To address this question, we consider a simpler rule called the 2-choices rule [Reference Cooper, Elsässer, Radzik, Esparza, Fraigniaud, Husfeldt and Koutsoupias6] for regular updates. Under the 2-choices rule, an agent samples two other agents from its neighborhood and updates to the majority opinion among the sampled agents and the agent itself. For graphs where the neighborhood sizes are large, this modified rule greatly reduces the communication overhead associated with computing the majority opinion since an agent no longer needs to know the opinions of all other agents in its neighborhood; only knowing the opinions of the two sampled agents suffices. The 2-choices rule also reduces the chance that an updating agent adopts the worse alternative when a majority of its neighbors have chosen this alternative. Hence, this modification should not only reduce the communication overhead but also “facilitate” consensus on the superior alternative. In this paper, we analytically characterize the improvement to the speed of consensus brought about by this modified rule.
Specifically, we show that if the network is a complete graph and the bias parameter α is sufficiently high (![]() $\alpha \gt 1/9$), then consensus is achieved on the superior opinion in
$\alpha \gt 1/9$), then consensus is achieved on the superior opinion in ![]() $\Theta(n\, \log n)$ time, where n denotes the number of agents in the network. When bias is small (i.e., when
$\Theta(n\, \log n)$ time, where n denotes the number of agents in the network. When bias is small (i.e., when ![]() $\alpha \lt 1/9$), we show that the consensus time depends on the initial configuration of the network. More specifically, when the bias parameter α is small, fast consensus (i.e.,
$\alpha \lt 1/9$), we show that the consensus time depends on the initial configuration of the network. More specifically, when the bias parameter α is small, fast consensus (i.e., ![]() $\Theta(n\, \log n)$ time) is achieved only if the initial proportion p of agents with the superior opinion is above a certain threshold value
$\Theta(n\, \log n)$ time) is achieved only if the initial proportion p of agents with the superior opinion is above a certain threshold value ![]() $p_c(\alpha)$ (explicitly characterized). If
$p_c(\alpha)$ (explicitly characterized). If ![]() $p \lt p_c(\alpha)$, we show that the network takes exponentially long time to reach consensus. Thus, the speed with which the network reaches consensus on the superior opinion undergoes a sharp phase transition depending on the values of α and p. Through simulations, we observe similar behavior on other classes of graphs, for example, on random d-regular graphs both with
$p \lt p_c(\alpha)$, we show that the network takes exponentially long time to reach consensus. Thus, the speed with which the network reaches consensus on the superior opinion undergoes a sharp phase transition depending on the values of α and p. Through simulations, we observe similar behavior on other classes of graphs, for example, on random d-regular graphs both with ![]() $d=\Theta(\log n)$ and Erdős–Rényi graphs with edge probability
$d=\Theta(\log n)$ and Erdős–Rényi graphs with edge probability ![]() $\Theta(\log n/n)$. To establish our theoretical results, we use a novel characterization of the expected number of visits of a random walk to a given state using a branching process. We expect this technique to be useful in the analysis of other interacting particle system models. Thus, in summary, our contributions are the following:
$\Theta(\log n/n)$. To establish our theoretical results, we use a novel characterization of the expected number of visits of a random walk to a given state using a branching process. We expect this technique to be useful in the analysis of other interacting particle system models. Thus, in summary, our contributions are the following:
• (Fast consensus) For complete graphs, we show the existence of a sharp threshold such that if the bias parameter α is above the threshold, then consensus is achieved on the superior opinion starting from any initial configuration in
 $\Theta(n\,\log n)$ time on average. If the bias parameter α is below the threshold, we show the existence of another sharp threshold such that if the initial proportion p of agents with the superior opinion is above this threshold, then consensus can be achieved in
$\Theta(n\,\log n)$ time on average. If the bias parameter α is below the threshold, we show the existence of another sharp threshold such that if the initial proportion p of agents with the superior opinion is above this threshold, then consensus can be achieved in  $\Theta(n\,\log n)$ time.
$\Theta(n\,\log n)$ time.• (Slow consensus) We show that when both the bias parameter α and the initial proportion p of agents with the superior opinion are below their corresponding thresholds, the average consensus time on complete graphs is
 $\Omega(\exp(\Theta(n)))$, that is, grows exponentially with the network size.
$\Omega(\exp(\Theta(n)))$, that is, grows exponentially with the network size.• (Other classes of graphs) Through extensive simulations, we study consensus on other classes of graphs. Specifically, we observe similar behavior on random d-regular graphs with
 $d=\Theta(\log n)$ and on Erdős–Rényi graphs with edge probability
$d=\Theta(\log n)$ and on Erdős–Rényi graphs with edge probability  $\log n/n$. For d-regular graphs with constant degrees
$\log n/n$. For d-regular graphs with constant degrees  $d=O(1)$, we do observe a phase transition, but the behavior below criticality is different from that in complete graphs or other dense graphs studied in this paper.
$d=O(1)$, we do observe a phase transition, but the behavior below criticality is different from that in complete graphs or other dense graphs studied in this paper.
1.1. Related Literature
The simplest model of opinion dynamics studied in the literature is the voter model, where an agent simply copies the opinion of an agent sampled randomly from its neighborhood. Thus, in the voter model, the probability that an agent adopts a specific opinion is equal to the proportion of agents having the same opinion in its neighborhood. Due to the linearity of the resulting dynamics and its duality with coalescing random walks, the voter model has been extensively studied in the literature. The duality between the voter model and coalescing random walks was first observed independently in [Reference Holley and Liggett14] and [Reference Clifford and Sudbury4]. Using this duality, the model has been analyzed on different classes of graphs such as regular lattices [Reference Cox7], random d-regular graphs [Reference Cooper, Elsasser, Ono and Radzik5], and Erdős–Rényi (ER) graphs [Reference Nakata, Imahayashi and Yamashita21]. It is known that for connected graphs, the probability of reaching consensus on the specific opinion is proportional to the initial volume (sum of degrees) of nodes having that opinion. It is also known that the mean consensus time for the asynchronous version of the voter model (where in each round only one randomly sampled agent updates its opinion) is ![]() $\Omega(n^2)$ for most graphs.
$\Omega(n^2)$ for most graphs.
Another important model of opinion dynamics is the majority rule model, wherein an agent adopts the majority opinion among all agents in its neighborhood. It was shown in [Reference Mossel, Neeman and Tamuz18] that with high probability for a family of expander graphs with sufficiently large spectral gap, the majority dynamics leads to a consensus on the opinion having the initial majority, provided that the imbalance between the initial majority opinion and the alternate opinion is sufficiently high. Bounds on the consensus time for the majority rule model was obtained in [Reference Zehmakan23] for expanders and ER random graphs. For expanders with sufficiently large spectral gaps, it was shown that consensus can be achieved on the initial majority opinion in ![]() $O(\log n)$ steps in the synchronous model where all agents update in each round. For ER graphs, it was shown that if the edge probability is above the connectivity threshold of
$O(\log n)$ steps in the synchronous model where all agents update in each round. For ER graphs, it was shown that if the edge probability is above the connectivity threshold of ![]() $\log n/n$, then consensus can be achieved on the initial majority opinion in constant number of rounds. The majority rule model has also been studied for other classes of graphs such as finite lattices [Reference Schonmann22], random regular graphs [Reference Gärtner, Zehmakan, Bender, Farach-Colton and Mosteiro13], and infinite trees [Reference Kanoria and Montanari15].
$\log n/n$, then consensus can be achieved on the initial majority opinion in constant number of rounds. The majority rule model has also been studied for other classes of graphs such as finite lattices [Reference Schonmann22], random regular graphs [Reference Gärtner, Zehmakan, Bender, Farach-Colton and Mosteiro13], and infinite trees [Reference Kanoria and Montanari15].
Although the majority rule leads to faster consensus on many classes of graphs, it requires an agent to know the states of all other agents in its neighborhood. This may be too computationally expensive when neighborhood sizes are large. A simpler alternative is to consider the 2-choices rule where an agent only samples two random neighburs and changes to the majority opinion among the sampled agents and the agent itself. Rules similar to the 2-choices rule, where groups of agents are formed at each instant and all agents in the group update to the majority opinion within the group, were analyzed in the physics literature [Reference Chen and Redner3, Reference Galam12, Reference Krapivsky and Redner16]. A generalization of 2-choices rule, where the updating agent samples m agents from its neighborhood and only changes its opinion if d or more of the sampled agent differ from the updating agent, was analyzed in the continuous time in [Reference Cruise and Ganesh10]. The 2-choices rule that we consider in this paper was first analyzed for random d-regular graphs and expanders in [Reference Cooper, Elsässer, Radzik, Esparza, Fraigniaud, Husfeldt and Koutsoupias6]. It was shown that consensus can be achieved in ![]() $O(\log n)$ time with high probability on the initial majority opinion, provided that the initial imbalance is sufficiently high.
$O(\log n)$ time with high probability on the initial majority opinion, provided that the initial imbalance is sufficiently high.
Opinion dynamical models with bias have been considered in the recent literature. These models are designed to capture the superiority of one alternative over another. Accordingly, in these models, the agents exhibit some form of bias toward the superior opinion. In [Reference Mukhopadhyay, Mazumdar and Roy19, Reference Mukhopadhyay, Mazumdar and Roy20], a weak form of bias is considered. Here, agents with the superior opinion update with a lesser frequency than agents with the alternative opinion. It has been shown in [Reference Mukhopadhyay, Mazumdar and Roy20] that, under the voter rule and the 2-choices rule, consensus is achieved in ![]() $O(\log n)$ time for complete graphs. For the voter model, the probability of achieving consensus on the superior opinion approaches to one as the network size grows. For the 2-choices rule, consensus is achieved on the superior opinion with high probability only when the initial proportion of agents with the superior opinion is above a certain threshold.
$O(\log n)$ time for complete graphs. For the voter model, the probability of achieving consensus on the superior opinion approaches to one as the network size grows. For the 2-choices rule, consensus is achieved on the superior opinion with high probability only when the initial proportion of agents with the superior opinion is above a certain threshold.
The form bias studied in this paper is introduced recently in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1, Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2]. These papers show that on dense graphs, the speed of consensus can be slow (depending on the minimum degree of a node) if the agents follow the majority rule during a regular update. The papers also analyze the voter rule under this form bias and show that consensus with the voter rule can be achieved in ![]() $O(n\, \log n)$ time. Our model is different from these models as we consider the 2-choices rule as the main update rule. Furthermore, we study the dynamics under the 2-choices rule as a function of the bias parameter α as well as the initial proportion p of agents with the superior opinion. This is unlike the previous papers [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1, Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2], where the dynamics is studied as a function of α only with a fixed value of p (specifically, p = 0). We show that phase transitions can occur with respect to both α and p. Similar phase transitions have been recently reported in [Reference Cruciani, Mimun, Quattropani and Rizzo8, Reference Cruciani, Natale, Nusser and Scornavacca9, Reference d’Amore, Ziccardi and Parter11] for noisy versions of the k-majority dynamics. However, the focus of these papers is a state of “near consensus” where both opinions coexist, but the proportion of agents with one of the opinions is arbitrarily small. In contrast, our results focus on the state of full consensus in which the inferior opinion is completely eliminated. Furthermore, we obtain bounds on the mean of the consensus time that are stronger than high probability bounds obtained in previous papers. The technique used here is also quite different from those used in the earlier works; while earlier works use concentration around the mean drift, we use suitably constructed branching processes to obtain bounds on the number of visits to different states.
$O(n\, \log n)$ time. Our model is different from these models as we consider the 2-choices rule as the main update rule. Furthermore, we study the dynamics under the 2-choices rule as a function of the bias parameter α as well as the initial proportion p of agents with the superior opinion. This is unlike the previous papers [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale, Rizzo and Bessiere1, Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2], where the dynamics is studied as a function of α only with a fixed value of p (specifically, p = 0). We show that phase transitions can occur with respect to both α and p. Similar phase transitions have been recently reported in [Reference Cruciani, Mimun, Quattropani and Rizzo8, Reference Cruciani, Natale, Nusser and Scornavacca9, Reference d’Amore, Ziccardi and Parter11] for noisy versions of the k-majority dynamics. However, the focus of these papers is a state of “near consensus” where both opinions coexist, but the proportion of agents with one of the opinions is arbitrarily small. In contrast, our results focus on the state of full consensus in which the inferior opinion is completely eliminated. Furthermore, we obtain bounds on the mean of the consensus time that are stronger than high probability bounds obtained in previous papers. The technique used here is also quite different from those used in the earlier works; while earlier works use concentration around the mean drift, we use suitably constructed branching processes to obtain bounds on the number of visits to different states.
1.2. Organization
The rest of the paper is organized as follows. In Section 2, we introduce the model studied in this paper. Next, in Section 3, we present the theoretical analysis of the model for complete graphs. Section 4 provides numerical results to support our theoretical findings and also demonstrates similar behavior for other classes of graphs. Finally, we conclude the paper in Section 5.
2. Model
In this section, we describe the model studied in this paper. The model consists of a network of n agents described by an undirected graph ![]() $G_n=(V_n,E_n)$, where the nodes in V n (with
$G_n=(V_n,E_n)$, where the nodes in V n (with ![]() $\lvert V_n \rvert=n$) represent the agents and the edges in E n represent the connections between the agents. For each agent (node)
$\lvert V_n \rvert=n$) represent the agents and the edges in E n represent the connections between the agents. For each agent (node) ![]() $u \in V_n$, we denote by
$u \in V_n$, we denote by ![]() $N_u = \left\{v:(u,v)\in E_n\right\}$, the set of neighbors of u.
$N_u = \left\{v:(u,v)\in E_n\right\}$, the set of neighbors of u.
Time is assumed to be discrete and at each discrete time instant ![]() $t \in \mathbb{Z}_+$, each agent is assumed to have an opinion in the set
$t \in \mathbb{Z}_+$, each agent is assumed to have an opinion in the set ![]() $\{0,1\}$. Without loss of generality, we assume that 1 is the superior opinion. Let
$\{0,1\}$. Without loss of generality, we assume that 1 is the superior opinion. Let ![]() $X_u(t) \in \{0,1\}$ denote the opinion of agent u at time t. At t = 0, the opinions of the agents are initialized such that
$X_u(t) \in \{0,1\}$ denote the opinion of agent u at time t. At t = 0, the opinions of the agents are initialized such that ![]() $\vert \{u\in V_n: X_u(0)=1\}\vert = \lceil pn \rceil$ for some
$\vert \{u\in V_n: X_u(0)=1\}\vert = \lceil pn \rceil$ for some ![]() $p \in [0,1)$. Hence, p fraction of agents initially have the superior opinion 1.
$p \in [0,1)$. Hence, p fraction of agents initially have the superior opinion 1.
At each instant ![]() $t \geq 0$, an agent, sampled uniformly at random, updates its opinion: with probability α, it performs a biased update in which it adopts the superior opinion irrespective of its current opinion and the opinions of all other agents; with probability
$t \geq 0$, an agent, sampled uniformly at random, updates its opinion: with probability α, it performs a biased update in which it adopts the superior opinion irrespective of its current opinion and the opinions of all other agents; with probability ![]() $1-\alpha$, it performs a regular update following the 2-choices rule in which the updating agent samples two neighbors uniformly at random (with replacementFootnote 1) and adopts the majority opinion among the sampled agents and the agent itself. Therefore, if U(t) denotes the randomly sampled agent at time t, then at time t + 1 the opinion of the agent is given by
$1-\alpha$, it performs a regular update following the 2-choices rule in which the updating agent samples two neighbors uniformly at random (with replacementFootnote 1) and adopts the majority opinion among the sampled agents and the agent itself. Therefore, if U(t) denotes the randomly sampled agent at time t, then at time t + 1 the opinion of the agent is given by
 \begin{equation}
X_{U(t)}(t+1)=\begin{cases}
1 & \text{w.p. } \alpha, \\
M(t) & \text{w.p. } 1-\alpha,
\end{cases}
\end{equation}
\begin{equation}
X_{U(t)}(t+1)=\begin{cases}
1 & \text{w.p. } \alpha, \\
M(t) & \text{w.p. } 1-\alpha,
\end{cases}
\end{equation}
where ![]() $M(t)={1}{\left(X_{U(t)}(t)+X_{N_1(t)}(t)+X_{N_2(t)}(t)\geq 2\right)}$ denotes the majority opinion among two randomly sampled neighbors
$M(t)={1}{\left(X_{U(t)}(t)+X_{N_1(t)}(t)+X_{N_2(t)}(t)\geq 2\right)}$ denotes the majority opinion among two randomly sampled neighbors ![]() $N_1(t)$ and
$N_1(t)$ and ![]() $N_2(t)$ of U(t) and the agent U(t) itself. The parameter
$N_2(t)$ of U(t) and the agent U(t) itself. The parameter ![]() $\alpha \in (0,1]$ represents the bias toward the superior opinion and is referred to as the bias parameter of the model.
$\alpha \in (0,1]$ represents the bias toward the superior opinion and is referred to as the bias parameter of the model.
The state of the network at any time ![]() $t \geq 0$ can be represented by the vector
$t \geq 0$ can be represented by the vector ![]() $\mathbf{X}(t)=(X_u(t), u \in V_n)$ of opinions of all the agents. The process
$\mathbf{X}(t)=(X_u(t), u \in V_n)$ of opinions of all the agents. The process ![]() $\mathbf{X}(\cdot)$ is Markov on the state space
$\mathbf{X}(\cdot)$ is Markov on the state space ![]() $\left\{0,1\right\}^n$ with a single absorbing state 1 where all agents have opinion 1. We refer to this absorbing state as the consensus state. Since it is possible to reach the consensus state from any other state in a finite number of steps, with probability one, the chain is absorbed in the consensus state in a finite time. We refer to this time as the consensus time. The objective of the rest of the paper is to analyze the mean consensus time for different values of the parameters
$\left\{0,1\right\}^n$ with a single absorbing state 1 where all agents have opinion 1. We refer to this absorbing state as the consensus state. Since it is possible to reach the consensus state from any other state in a finite number of steps, with probability one, the chain is absorbed in the consensus state in a finite time. We refer to this time as the consensus time. The objective of the rest of the paper is to analyze the mean consensus time for different values of the parameters ![]() $n,\alpha,p$ and for different classes of graphs.
$n,\alpha,p$ and for different classes of graphs.
3. Analysis for complete graphs
In this section, we assume that G n is a complete graph on n nodes. For complete graphs, the process ![]() $\bar X^n=(\bar X^n(t)=\vert \{u\in V_n: X_u(t)=1\} \vert,\ t\geq 0)$ counting the number of agents with opinion 1 is a Markov chain on
$\bar X^n=(\bar X^n(t)=\vert \{u\in V_n: X_u(t)=1\} \vert,\ t\geq 0)$ counting the number of agents with opinion 1 is a Markov chain on ![]() $\mathbb{Z}_+$ with absorbing state n. For the chain
$\mathbb{Z}_+$ with absorbing state n. For the chain ![]() $\bar X^n$, the transition probability
$\bar X^n$, the transition probability ![]() $\tilde{p}_{i,j}$ from state i to j is given by
$\tilde{p}_{i,j}$ from state i to j is given by ![]() $\tilde p_{i,j}={p}_{i,j}+o(1/n)$, where
$\tilde p_{i,j}={p}_{i,j}+o(1/n)$, where
 \begin{equation}
p_{i,j}=\begin{cases}
\left(1-\frac{i}{n}\right)\left(\alpha+(1-\alpha)\left(\frac{i}{n}\right)^2\right), &\text{if } j=i+1,\\
\frac{i}{n}(1-\alpha)\left(1-\frac{i}{n}\right)^2, &\text{if } j=i-1,\\
1-p_{i,i+1}-p_{i,i-1}, &\text{if } j=i,\\
0, &\text{otherwise.}
\end{cases}
\end{equation}
\begin{equation}
p_{i,j}=\begin{cases}
\left(1-\frac{i}{n}\right)\left(\alpha+(1-\alpha)\left(\frac{i}{n}\right)^2\right), &\text{if } j=i+1,\\
\frac{i}{n}(1-\alpha)\left(1-\frac{i}{n}\right)^2, &\text{if } j=i-1,\\
1-p_{i,i+1}-p_{i,i-1}, &\text{if } j=i,\\
0, &\text{otherwise.}
\end{cases}
\end{equation}
Note that ![]() $p_{i,j}$ denotes the transition probability of a slightly modified chain
$p_{i,j}$ denotes the transition probability of a slightly modified chain ![]() $\bar Y^n$ (with the same absorbing state n), where an agent during a regular update can sample itself in addition to its neighbors. Further we analyze this modified chain as it is simpler to do so and the asymptotic (in n) results we obtain for this modified chain also hold for the original chain (see Remark 3.7 for more explanation).
$\bar Y^n$ (with the same absorbing state n), where an agent during a regular update can sample itself in addition to its neighbors. Further we analyze this modified chain as it is simpler to do so and the asymptotic (in n) results we obtain for this modified chain also hold for the original chain (see Remark 3.7 for more explanation).
Below we characterize the scaling law of ![]() $\bar T_n(p)=\mathbb{E}_{\lceil pn \rceil}[T_n]$, where
$\bar T_n(p)=\mathbb{E}_{\lceil pn \rceil}[T_n]$, where ![]() $\mathbb{E}_{x}\left[\cdot\right]$ denotes expectation conditioned on
$\mathbb{E}_{x}\left[\cdot\right]$ denotes expectation conditioned on ![]() $\bar Y^n(0)=x$ and
$\bar Y^n(0)=x$ and ![]() $T_k=\inf\{t\geq 0: \bar Y^n(t)=k\}$ denotes the first time the network reaches state k. Our main result is described in Theorem 3.1.
$T_k=\inf\{t\geq 0: \bar Y^n(t)=k\}$ denotes the first time the network reaches state k. Our main result is described in Theorem 3.1.
Theorem 3.1 For complete graphs, we have the following
1. (Fast consensus) For each
 $\alpha \in (1/9,1)$, we have
$\alpha \in (1/9,1)$, we have  $\bar T_n(p) = \Theta(n\, \log n)$ for all
$\bar T_n(p) = \Theta(n\, \log n)$ for all  $p \in [0,1)$.
$p \in [0,1)$.2. (Fast consensus) For each
 $\alpha \in (0, 1/9)$, there exists
$\alpha \in (0, 1/9)$, there exists  $p_c(\alpha) \in (0,1)$ such that if
$p_c(\alpha) \in (0,1)$ such that if  $p \in [p_c(\alpha),1)$, then
$p \in [p_c(\alpha),1)$, then  $\bar T_n(p)=\Theta(n\, \log n)$. Furthermore, the threshold
$\bar T_n(p)=\Theta(n\, \log n)$. Furthermore, the threshold  $p_c(\alpha)$ is the unique solution in the range
$p_c(\alpha)$ is the unique solution in the range  $(\bar x_\alpha,1)$ of the equation(3)where
$(\bar x_\alpha,1)$ of the equation(3)where \begin{equation}
\int_{\bar{x}_\alpha}^{p_c(\alpha)} \log(f_\alpha(x))dx =0,
\end{equation}
\begin{equation}
\int_{\bar{x}_\alpha}^{p_c(\alpha)} \log(f_\alpha(x))dx =0,
\end{equation}
 $f_\alpha(x)=\frac{(1-\alpha)x(1-x)}{\alpha+(1-\alpha)x^2}$,
$f_\alpha(x)=\frac{(1-\alpha)x(1-x)}{\alpha+(1-\alpha)x^2}$,  $\bar{x}_{\alpha}=\frac{1}{4}\left(1-\sqrt{1-\frac{8\alpha}{1-\alpha}}\right)$, and
$\bar{x}_{\alpha}=\frac{1}{4}\left(1-\sqrt{1-\frac{8\alpha}{1-\alpha}}\right)$, and  $\bar x_\alpha =\frac{1}{4}\left(1+\sqrt{1-\frac{8\alpha}{1-\alpha}}\right)$.
$\bar x_\alpha =\frac{1}{4}\left(1+\sqrt{1-\frac{8\alpha}{1-\alpha}}\right)$.
3. (Slow consensus) For each
 $\alpha \in (0,1/9)$ and
$\alpha \in (0,1/9)$ and  $p \in [0,p_c(\alpha))$, we have
$p \in [0,p_c(\alpha))$, we have  $\bar T_n(p)=\Omega(\exp(\Theta(n)))$.
$\bar T_n(p)=\Omega(\exp(\Theta(n)))$.
The above theorem implies that when the bias parameter is sufficiently high (![]() $\alpha \gt1/9$), the network quickly (in
$\alpha \gt1/9$), the network quickly (in ![]() $\Theta(n\, \log n)$ time) reaches consensus on the superior opinion irrespective of its initial state. This is in sharp contrast to the result of [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2], where the consensus time is exponential in n for all values of the bias parameter α. The theorem further implies that even with low value of the bias parameter α (for
$\Theta(n\, \log n)$ time) reaches consensus on the superior opinion irrespective of its initial state. This is in sharp contrast to the result of [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2], where the consensus time is exponential in n for all values of the bias parameter α. The theorem further implies that even with low value of the bias parameter α (for ![]() $\alpha \lt 1/9$), fast consensus can be achieved as long as the initial proportion p of agents with the superior opinion is above a threshold value denoted by
$\alpha \lt 1/9$), fast consensus can be achieved as long as the initial proportion p of agents with the superior opinion is above a threshold value denoted by ![]() $p_c(\alpha)$. We explicitly characterize this threshold
$p_c(\alpha)$. We explicitly characterize this threshold ![]() $p_c(\alpha)$ required to ensure fast consensus when the bias is low. If the bias parameter is low (
$p_c(\alpha)$ required to ensure fast consensus when the bias is low. If the bias parameter is low (![]() $\alpha \lt 1/9$) and the initial proportion of agents with the superior opinion is below the threshold, that is,
$\alpha \lt 1/9$) and the initial proportion of agents with the superior opinion is below the threshold, that is, ![]() $p \lt p_c(\alpha)$, then the mean consensus time is exponential in n, which corresponds to slow speed of convergence. Thus, our model exhibits rich behavior in terms of the parameters α and p.
$p \lt p_c(\alpha)$, then the mean consensus time is exponential in n, which corresponds to slow speed of convergence. Thus, our model exhibits rich behavior in terms of the parameters α and p.
We breakdown the proof of the above theorem into several simpler steps. The first step is to make the following simple observation, which expresses the mean consensus time as a function of the number of visits of the chain ![]() $\bar Y^n$ to different states in its state-space
$\bar Y^n$ to different states in its state-space ![]() $\{0,1,\ldots,n\}$.
$\{0,1,\ldots,n\}$.
Lemma 3.2 Let Z k denote the number of visits of the chain ![]() $\bar Y^n$ to the state
$\bar Y^n$ to the state ![]() $k \in \{0,1,\ldots,n\}$ before absorption. Then, for any starting state
$k \in \{0,1,\ldots,n\}$ before absorption. Then, for any starting state ![]() $x =\bar{X}^n(0)\in \{0,1,\ldots,n\}$, the average consensus time is given by
$x =\bar{X}^n(0)\in \{0,1,\ldots,n\}$, the average consensus time is given by
 \begin{equation}
\mathbb{E}_{x}\left[T_n\right] =\sum_{k=0}^{n-1} \frac{\mathbb{E}_{x}\left[Z_k\right]}{(1-p_{k,k})},
\end{equation}
\begin{equation}
\mathbb{E}_{x}\left[T_n\right] =\sum_{k=0}^{n-1} \frac{\mathbb{E}_{x}\left[Z_k\right]}{(1-p_{k,k})},
\end{equation}
where ![]() $p_{k,k}$ is the transition probability from state k to itself given by Eq. (2).
$p_{k,k}$ is the transition probability from state k to itself given by Eq. (2).
Proof. Observe that the consensus time T n can be written as
 \begin{equation}
T_n=\sum_{k=0}^{n-1}\sum_{j=1}^{Z_k} M_{k,j},
\end{equation}
\begin{equation}
T_n=\sum_{k=0}^{n-1}\sum_{j=1}^{Z_k} M_{k,j},
\end{equation}
where Z k denotes the number of visits to state k before absorption and ![]() $M_{k,j}$ denotes the time spent in state k in the
$M_{k,j}$ denotes the time spent in state k in the ![]() $j{\textrm{th}}$ visit. Clearly, the random variables Z k and
$j{\textrm{th}}$ visit. Clearly, the random variables Z k and ![]() $(M_{k,j})_{j\geq 1}$ are independent of each other. Furthermore,
$(M_{k,j})_{j\geq 1}$ are independent of each other. Furthermore, ![]() $(M_{k,j})_{j\geq 1}$ is a sequence of i.i.d. random variables with geometric distribution given by
$(M_{k,j})_{j\geq 1}$ is a sequence of i.i.d. random variables with geometric distribution given by  $\mathbb{P}_{x}(M_{k,j}=i)=p_{k,k}^{i-1}(1-p_{k,k})$ for all j. Hence, applying Wald’s identity to Eq. (5), we have
$\mathbb{P}_{x}(M_{k,j}=i)=p_{k,k}^{i-1}(1-p_{k,k})$ for all j. Hence, applying Wald’s identity to Eq. (5), we have
 \begin{align}
\bar T_{n}(p) &=\mathbb{E}_{x}\left[T_n\right] \nonumber\\
&=\sum_{k=0}^{n-1}\mathbb{E}_{x}\left[\sum_{j=1}^{Z_k}M_{k,j}\right]\nonumber\\
&=\sum_{k=0}^{n-1} \mathbb{E}_{x}\left[Z_k\right] \mathbb{E}_{x}\left[M_{k,j}\right] \nonumber\\
&=\sum_{k=0}^{n-1} \frac{\mathbb{E}_{x}\left[Z_k\right]}{(1-p_{k,k})},
\end{align}
\begin{align}
\bar T_{n}(p) &=\mathbb{E}_{x}\left[T_n\right] \nonumber\\
&=\sum_{k=0}^{n-1}\mathbb{E}_{x}\left[\sum_{j=1}^{Z_k}M_{k,j}\right]\nonumber\\
&=\sum_{k=0}^{n-1} \mathbb{E}_{x}\left[Z_k\right] \mathbb{E}_{x}\left[M_{k,j}\right] \nonumber\\
&=\sum_{k=0}^{n-1} \frac{\mathbb{E}_{x}\left[Z_k\right]}{(1-p_{k,k})},
\end{align}
where the last step follows from the fact that ![]() $\mathbb{E}_{x}[M_{k,j}]=1/(1-p_{k,k})$ for each
$\mathbb{E}_{x}[M_{k,j}]=1/(1-p_{k,k})$ for each ![]() $j \in [Z_k]$.
$j \in [Z_k]$.
From the above lemma, it is evident that in order to obtain bounds on ![]() $\mathbb{E}_{x}[T_n]$, we need to obtain bounds of the expected number of visits
$\mathbb{E}_{x}[T_n]$, we need to obtain bounds of the expected number of visits ![]() $\mathbb{E}_{x}[Z_k]$ to different states and the transition probabilities
$\mathbb{E}_{x}[Z_k]$ to different states and the transition probabilities ![]() $p_{k,k}$. Using this approach, we first obtain a lower bound on
$p_{k,k}$. Using this approach, we first obtain a lower bound on ![]() $\bar T_n(p)$.
$\bar T_n(p)$.
Lemma 3.3 For any ![]() $\alpha \in (0,1)$ and
$\alpha \in (0,1)$ and ![]() $p \in (0,1)$, we have
$p \in (0,1)$, we have ![]() $\bar T_n(p)=\Omega(n \log n)$.
$\bar T_n(p)=\Omega(n \log n)$.
Proof. From Eq. (2), we obtain
 \begin{align*}
1-p_{k,k} &= \left(1-\frac{k}{n}\right)\left(\alpha+\left(1-\alpha\right)\frac{k}{n}\right)\\
&\leq \max\left(\alpha,1-\alpha\right) \left(1-\frac{k}{n}\right)\left(1+\frac{k}{n}\right).r_\alpha
\end{align*}
\begin{align*}
1-p_{k,k} &= \left(1-\frac{k}{n}\right)\left(\alpha+\left(1-\alpha\right)\frac{k}{n}\right)\\
&\leq \max\left(\alpha,1-\alpha\right) \left(1-\frac{k}{n}\right)\left(1+\frac{k}{n}\right).r_\alpha
\end{align*}
Furthermore, we have ![]() $\mathbb{E}_{x}[Z_k] \geq {1}{(k \geq x)}$ since states
$\mathbb{E}_{x}[Z_k] \geq {1}{(k \geq x)}$ since states ![]() $k \geq x$ are visited at least once. Hence, using the above two inequalities in Eq. (4), we obtain
$k \geq x$ are visited at least once. Hence, using the above two inequalities in Eq. (4), we obtain
 \begin{align*}
\bar T_n(p) & \geq \sum_{k=0}^{n-1} \frac{{1}{\left(k \geq \lceil np \rceil\right)}}{\max\left(\alpha,1-\alpha\right) \left(1-\frac{k}{n}\right)\left(1+\frac{k}{n}\right)}\\
& = \frac{n}{2\max\left(\alpha,1-\alpha\right)}\sum_{k=\lceil np \rceil}^{n-1}\left(\frac{1}{n-k}+\frac{1}{n+k}\right)\\
& \gt \frac{n}{2\max\left(\alpha,1-\alpha\right)}\sum_{k=\lceil np \rceil}^{n-1}\left(\frac{1}{n-k}\right)\\
& \geq \frac{n}{2\max\left(\alpha,1-\alpha\right)}\log\left(n-\lceil np \rceil+1\right),
\end{align*}
\begin{align*}
\bar T_n(p) & \geq \sum_{k=0}^{n-1} \frac{{1}{\left(k \geq \lceil np \rceil\right)}}{\max\left(\alpha,1-\alpha\right) \left(1-\frac{k}{n}\right)\left(1+\frac{k}{n}\right)}\\
& = \frac{n}{2\max\left(\alpha,1-\alpha\right)}\sum_{k=\lceil np \rceil}^{n-1}\left(\frac{1}{n-k}+\frac{1}{n+k}\right)\\
& \gt \frac{n}{2\max\left(\alpha,1-\alpha\right)}\sum_{k=\lceil np \rceil}^{n-1}\left(\frac{1}{n-k}\right)\\
& \geq \frac{n}{2\max\left(\alpha,1-\alpha\right)}\log\left(n-\lceil np \rceil+1\right),
\end{align*}
which completes the proof.
To obtain an upper bound on the mean consensus time ![]() $\bar T_n(p)$ similarly, we need an upper bound on the expected number of visits
$\bar T_n(p)$ similarly, we need an upper bound on the expected number of visits ![]() $\mathbb{E}_{x}\left[Z_k\right]$ to state k for each
$\mathbb{E}_{x}\left[Z_k\right]$ to state k for each ![]() $k \in \left\{0,1,2,\ldots,n\right\}$. We obtain such an upper bound using a technique developed in [Reference Mukhopadhyay, Mazumdar and Roy20], where the number of visits to each state is expressed as a function of a branching process. Specifically, we define ζ k to be the number of jumps from state k to state k − 1 for any
$k \in \left\{0,1,2,\ldots,n\right\}$. We obtain such an upper bound using a technique developed in [Reference Mukhopadhyay, Mazumdar and Roy20], where the number of visits to each state is expressed as a function of a branching process. Specifically, we define ζ k to be the number of jumps from state k to state k − 1 for any ![]() $k\in \{1,2,\ldots,n\}$. Clearly,
$k\in \{1,2,\ldots,n\}$. Clearly, ![]() $\zeta_n=0$, and if the starting state is
$\zeta_n=0$, and if the starting state is ![]() $x=\bar Y^n(0) \in [1,n)$, then ζ k satisfies the following recursion:
$x=\bar Y^n(0) \in [1,n)$, then ζ k satisfies the following recursion:
 \begin{equation}
\zeta_k=\begin{cases}
\sum_{l=0}^{\zeta_{k+1}}\xi_{l,k}, &\text{if } k \in \{x,x+1,\ldots,n-1\},\\
\sum_{l=1}^{\zeta_{k+1}}\xi_{l,k}, &\text{if } k \in \{0,1,\ldots,x-1\},
\end{cases}
\end{equation}
\begin{equation}
\zeta_k=\begin{cases}
\sum_{l=0}^{\zeta_{k+1}}\xi_{l,k}, &\text{if } k \in \{x,x+1,\ldots,n-1\},\\
\sum_{l=1}^{\zeta_{k+1}}\xi_{l,k}, &\text{if } k \in \{0,1,\ldots,x-1\},
\end{cases}
\end{equation}
where ![]() $\xi_{l,k}$ denotes the number of jumps from state k to state k − 1 between the
$\xi_{l,k}$ denotes the number of jumps from state k to state k − 1 between the ![]() $l{\textrm{th}}$ and
$l{\textrm{th}}$ and ![]() $(l+1){\textrm{th}}$ visit to state k + 1. Note that the first sum in Eq. (7) (for
$(l+1){\textrm{th}}$ visit to state k + 1. Note that the first sum in Eq. (7) (for ![]() $k \geq x$) starts from l = 0, whereas the second sum starts from l = 1. This is because for
$k \geq x$) starts from l = 0, whereas the second sum starts from l = 1. This is because for ![]() $k\geq x$, jumps from k to k − 1 can occur even before the first jump from k + 1 to k. This is not the case for states k < x. Furthermore,
$k\geq x$, jumps from k to k − 1 can occur even before the first jump from k + 1 to k. This is not the case for states k < x. Furthermore, ![]() $\{\xi_{l,k}\}_{l\geq 0}$ is a sequence of i.i.d. random variables independent of
$\{\xi_{l,k}\}_{l\geq 0}$ is a sequence of i.i.d. random variables independent of ![]() $\zeta_{k+1}$. Hence, the sequence
$\zeta_{k+1}$. Hence, the sequence ![]() $\{\xi_{n-k}\}_k$ defines a branching process. Moreover, the number of visits to state k can be written as
$\{\xi_{n-k}\}_k$ defines a branching process. Moreover, the number of visits to state k can be written as
 \begin{equation}
{Z_k} = \begin{cases}
1+\zeta_k+\zeta_{k+1}, &\text{if } k \in \{x,x+1,\ldots,n-1\},\\
\zeta_k+\zeta_{k+1}, &\text{if } k \in \{0,1,\ldots,x-1\},
\end{cases}
\end{equation}
\begin{equation}
{Z_k} = \begin{cases}
1+\zeta_k+\zeta_{k+1}, &\text{if } k \in \{x,x+1,\ldots,n-1\},\\
\zeta_k+\zeta_{k+1}, &\text{if } k \in \{0,1,\ldots,x-1\},
\end{cases}
\end{equation}
where the additional one appears in the first case (for ![]() $k \geq x$) because the states
$k \geq x$) because the states ![]() $k \geq x$ are visited at least once before the chain is absorbed in state n. It is the above characterization of the Z k that we shall use to obtain upper bounds on
$k \geq x$ are visited at least once before the chain is absorbed in state n. It is the above characterization of the Z k that we shall use to obtain upper bounds on ![]() $\mathbb{E}_{x}[Z_k]$. Precisely, we obtain bounds on
$\mathbb{E}_{x}[Z_k]$. Precisely, we obtain bounds on ![]() $\mathbb{E}_{x}[\zeta_k]$ to bound
$\mathbb{E}_{x}[\zeta_k]$ to bound ![]() $\mathbb{E}_{x}[Z_k]$. In the lemma below, we express
$\mathbb{E}_{x}[Z_k]$. In the lemma below, we express ![]() $\mathbb{E}_{x}[\zeta_k]$ in terms of the transition probabilities of the chain
$\mathbb{E}_{x}[\zeta_k]$ in terms of the transition probabilities of the chain ![]() $\bar{Y}^n$.
$\bar{Y}^n$.
Lemma 3.4 For any ![]() $k\in \{1,2,\ldots,n\}$, let ζ k denote the number of jumps of the chain
$k\in \{1,2,\ldots,n\}$, let ζ k denote the number of jumps of the chain ![]() $\bar Y^n$ from state k to state k − 1. We have
$\bar Y^n$ from state k to state k − 1. We have ![]() $\zeta_n=0$ and
$\zeta_n=0$ and
 \begin{equation}
\mathbb{E}_{x}\left[\zeta_{k}\right]=\begin{cases}
\sum_{t=k}^{n-1} \prod_{i=k}^{t} \frac{p_{i,i-1}}{p_{i,i+1}}, \quad \text{for } x \leq k \leq n-1,\\
\left(\prod_{i=k}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}\right)\mathbb{E}_{x}\left[\zeta_{x}\right], \quad \text{for } 0 \leq k \lt x,
\end{cases}
\end{equation}
\begin{equation}
\mathbb{E}_{x}\left[\zeta_{k}\right]=\begin{cases}
\sum_{t=k}^{n-1} \prod_{i=k}^{t} \frac{p_{i,i-1}}{p_{i,i+1}}, \quad \text{for } x \leq k \leq n-1,\\
\left(\prod_{i=k}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}\right)\mathbb{E}_{x}\left[\zeta_{x}\right], \quad \text{for } 0 \leq k \lt x,
\end{cases}
\end{equation}
where for each ![]() $i, j \in \{0,1,\ldots,n\}$,
$i, j \in \{0,1,\ldots,n\}$, ![]() $p_{i,j}$ denotes the transition probability of the Markov chain
$p_{i,j}$ denotes the transition probability of the Markov chain ![]() $\bar Y^n$ from state i to state j and is given by Eq. (2).
$\bar Y^n$ from state i to state j and is given by Eq. (2).
Proof. We observe that ![]() $\zeta_{k+1}$ and
$\zeta_{k+1}$ and  $\left\{\xi_{l,k}\right\}_{l\geq 0}$ are independent of each other and
$\left\{\xi_{l,k}\right\}_{l\geq 0}$ are independent of each other and  $\left\{\xi_{l,k}\right\}_{l\geq 0}$ is a sequence of i.i.d. random variables with
$\left\{\xi_{l,k}\right\}_{l\geq 0}$ is a sequence of i.i.d. random variables with
 \begin{equation*}\mathbb{P}_{x}\left(\xi_{l,k}=i\right)=\left(\frac{p_{k,k-1}}{1-p_{k,k}}\right)^i\left(\frac{p_{k,k+1}}{1-p_{k,k}}\right)\end{equation*}
\begin{equation*}\mathbb{P}_{x}\left(\xi_{l,k}=i\right)=\left(\frac{p_{k,k-1}}{1-p_{k,k}}\right)^i\left(\frac{p_{k,k+1}}{1-p_{k,k}}\right)\end{equation*}for all ![]() $i \in \mathbb{Z}_+$ and all
$i \in \mathbb{Z}_+$ and all ![]() $l \geq 0$. Hence, we have
$l \geq 0$. Hence, we have
 \begin{equation*}\mathbb{E}_{x}\left[\xi_{l,k}\right]=\frac{p_{k,k-1}}{p_{k,k+1}},\end{equation*}
\begin{equation*}\mathbb{E}_{x}\left[\xi_{l,k}\right]=\frac{p_{k,k-1}}{p_{k,k+1}},\end{equation*}for all ![]() $l \geq 0$. Applying Wald’s identity to Eq. (7), we obtain the following recursions
$l \geq 0$. Applying Wald’s identity to Eq. (7), we obtain the following recursions
 \begin{equation}
\mathbb{E}_{x}\left[\zeta_k\right]=\begin{cases}
\left(1+\mathbb{E}_{x}\left[\zeta_{k+1}\right]\right)\frac{p_{k,k-1}}{p_{k,k+1}}, &\text{if } k \geq x,\\
\mathbb{E}_{x}\left[\zeta_{k+1}\right]\frac{p_{k,k-1}}{p_{k,k+1}}, &\text{if } k \lt x,
\end{cases}
\end{equation}
\begin{equation}
\mathbb{E}_{x}\left[\zeta_k\right]=\begin{cases}
\left(1+\mathbb{E}_{x}\left[\zeta_{k+1}\right]\right)\frac{p_{k,k-1}}{p_{k,k+1}}, &\text{if } k \geq x,\\
\mathbb{E}_{x}\left[\zeta_{k+1}\right]\frac{p_{k,k-1}}{p_{k,k+1}}, &\text{if } k \lt x,
\end{cases}
\end{equation}
Upon solving the above recursions with boundary condition ![]() ${\zeta_n}=0$, we obtain desired result.
${\zeta_n}=0$, we obtain desired result.
From Eq. (9), we observe that the ratio ![]() $p_{i,i-1}/p_{i,i+1}$ plays a crucial role in the expression of
$p_{i,i-1}/p_{i,i+1}$ plays a crucial role in the expression of ![]() $\mathbb{E}_{x}\left[\zeta_k\right]$. Hence, by characterizing this ratio, we can characterize
$\mathbb{E}_{x}\left[\zeta_k\right]$. Hence, by characterizing this ratio, we can characterize ![]() $\mathbb{E}_{x}\left[\zeta_k\right]$. We note from Eq. (2) that
$\mathbb{E}_{x}\left[\zeta_k\right]$. We note from Eq. (2) that
 \begin{equation}
\frac{p_{i,i-1}}{p_{i,i+1}}=f_\alpha(i/n),
\end{equation}
\begin{equation}
\frac{p_{i,i-1}}{p_{i,i+1}}=f_\alpha(i/n),
\end{equation}
where ![]() $f_\alpha:[0,1]\to \mathbb{R}_+$, for each
$f_\alpha:[0,1]\to \mathbb{R}_+$, for each ![]() $\alpha \in (0,1)$, is as defined in Theorem 3.1. In the lemma below, we obtain a list of some important properties of the function f α.
$\alpha \in (0,1)$, is as defined in Theorem 3.1. In the lemma below, we obtain a list of some important properties of the function f α.
Lemma 3.5 For ![]() $\alpha \in (0,1)$, define
$\alpha \in (0,1)$, define ![]() $f_\alpha:[0,1]\to \mathbb{R}_+$
$f_\alpha:[0,1]\to \mathbb{R}_+$
 \begin{equation}
f_\alpha(x)\triangleq\frac{(1-\alpha)x(1-x)}{\alpha+(1-\alpha)x^2}.
\end{equation}
\begin{equation}
f_\alpha(x)\triangleq\frac{(1-\alpha)x(1-x)}{\alpha+(1-\alpha)x^2}.
\end{equation}
Then f α satisfies the following properties
1. For all
 $\alpha \in (0,1)$, f α is strictly increasing in
$\alpha \in (0,1)$, f α is strictly increasing in  $[0,x_\alpha)$, strictly decreasing in
$[0,x_\alpha)$, strictly decreasing in  $(x_\alpha, 1]$, and, in the domain
$(x_\alpha, 1]$, and, in the domain  $[0,1]$, attains its maximum value at x α, where
(13)
$[0,1]$, attains its maximum value at x α, where
(13) \begin{equation}
x_\alpha\triangleq \sqrt{\left(\frac{\alpha}{1-\alpha}\right)^2+\frac{\alpha}{1-\alpha}}-\frac{\alpha}{1-\alpha} \in [0,1).
\end{equation}
\begin{equation}
x_\alpha\triangleq \sqrt{\left(\frac{\alpha}{1-\alpha}\right)^2+\frac{\alpha}{1-\alpha}}-\frac{\alpha}{1-\alpha} \in [0,1).
\end{equation}
2. Let
 $r_\alpha\triangleq f_\alpha(x_\alpha)=\max_{x \in [0,1]}f_\alpha(x)$. Then, for
$r_\alpha\triangleq f_\alpha(x_\alpha)=\max_{x \in [0,1]}f_\alpha(x)$. Then, for  $\alpha \in (1/9,1)$, we have
$\alpha \in (1/9,1)$, we have  $r_\alpha \lt 1$, and for
$r_\alpha \lt 1$, and for  $\alpha \in (0,1/9)$, we have
$\alpha \in (0,1/9)$, we have  $r_\alpha \gt 1$.
$r_\alpha \gt 1$.3. For
 $\alpha \in (0,1/9]$, we have
$\alpha \in (0,1/9]$, we have  $f_\alpha(x) \geq 1$ iff
$f_\alpha(x) \geq 1$ iff  $x \in [\underline{x}_{\alpha},\bar{x}_\alpha]$, where(14)
$x \in [\underline{x}_{\alpha},\bar{x}_\alpha]$, where(14) \begin{align}
\underline{x}_\alpha &= \frac{1}{4}\left(1-\sqrt{1-\frac{8\alpha}{1-\alpha}}\right),
\end{align}
(15)
\begin{align}
\underline{x}_\alpha &= \frac{1}{4}\left(1-\sqrt{1-\frac{8\alpha}{1-\alpha}}\right),
\end{align}
(15) \begin{align}
\bar x_\alpha &=\frac{1}{4}\left(1+\sqrt{1-\frac{8\alpha}{1-\alpha}}\right).
\end{align}
\begin{align}
\bar x_\alpha &=\frac{1}{4}\left(1+\sqrt{1-\frac{8\alpha}{1-\alpha}}\right).
\end{align}
Furthermore,
 $f_\alpha(\underline{x}_\alpha)=f_\alpha(\bar{x}_\alpha)=1$ and
$f_\alpha(\underline{x}_\alpha)=f_\alpha(\bar{x}_\alpha)=1$ and  $x_\alpha \in [\underline{x}_{\alpha},\bar{x}_\alpha]$.
$x_\alpha \in [\underline{x}_{\alpha},\bar{x}_\alpha]$.4. For
 $\alpha \in (0,1/9)$, define
$\alpha \in (0,1/9)$, define  $g_\alpha(x)\triangleq\int_{\underline{x}_\alpha}^x \log(\ f_\alpha(x))\,{\rm d}x$. Then g α has a unique root
$g_\alpha(x)\triangleq\int_{\underline{x}_\alpha}^x \log(\ f_\alpha(x))\,{\rm d}x$. Then g α has a unique root  $p_c(\alpha) \in (\bar x_\alpha,1)$. Furthermore,
$p_c(\alpha) \in (\bar x_\alpha,1)$. Furthermore,  $g_\alpha(p) \gt 0$ if
$g_\alpha(p) \gt 0$ if  $p \in [\bar x_\alpha, p_c(\alpha))$ and
$p \in [\bar x_\alpha, p_c(\alpha))$ and  $g_\alpha(p) \lt 0$ if
$g_\alpha(p) \lt 0$ if  $p \in (p_c(\alpha),1).$
$p \in (p_c(\alpha),1).$
Proof. Taking the derivative of Eq. (12) with respect x, we obtain
 \begin{equation*}
f_\alpha^\prime(x)=\frac{-(1-\alpha)^2 x^2-2\alpha(1-\alpha)x+\alpha(1-\alpha)}{\left(\alpha+(1-\alpha)x^2\right)^2}.
\end{equation*}
\begin{equation*}
f_\alpha^\prime(x)=\frac{-(1-\alpha)^2 x^2-2\alpha(1-\alpha)x+\alpha(1-\alpha)}{\left(\alpha+(1-\alpha)x^2\right)^2}.
\end{equation*}
We note that the numerator of the above expression is zero when ![]() $x=x_\alpha$, positive when
$x=x_\alpha$, positive when ![]() $x \in [0, x_\alpha)$, and negative when
$x \in [0, x_\alpha)$, and negative when ![]() $x \in (x_\alpha, 1]$, where x α is as defined in Eq. (13). This proves the first statement of the lemma.
$x \in (x_\alpha, 1]$, where x α is as defined in Eq. (13). This proves the first statement of the lemma.
Next, we note from Eq. (12) that the condition ![]() $f_\alpha(x) \lesseqgtr 1$ is equivalent to
$f_\alpha(x) \lesseqgtr 1$ is equivalent to  $2x^2-x+\frac{\alpha}{1-\alpha} \gtreqless 0$. Hence,
$2x^2-x+\frac{\alpha}{1-\alpha} \gtreqless 0$. Hence, ![]() $f_\alpha(x) \lt 1$ for all
$f_\alpha(x) \lt 1$ for all ![]() $x \in [0,1]$ if and only if
$x \in [0,1]$ if and only if ![]() $1-8\frac{\alpha}{1-\alpha} \lt0$ or equivalently iff
$1-8\frac{\alpha}{1-\alpha} \lt0$ or equivalently iff ![]() $\alpha \gt 1/9$. Furthermore, for
$\alpha \gt 1/9$. Furthermore, for ![]() $\alpha \in (0,1/9]$, we have
$\alpha \in (0,1/9]$, we have  $2x^2-x+\frac{\alpha}{1-\alpha}=(x-\underline{x}_\alpha)(x-\bar x_\alpha)$, where
$2x^2-x+\frac{\alpha}{1-\alpha}=(x-\underline{x}_\alpha)(x-\bar x_\alpha)$, where ![]() $\underline{x}_\alpha$ and
$\underline{x}_\alpha$ and ![]() $\bar{x}_\alpha$ are as defined in Eqs. (14) and (15), respectively, and for
$\bar{x}_\alpha$ are as defined in Eqs. (14) and (15), respectively, and for ![]() $\alpha \lt 1/9$, we have
$\alpha \lt 1/9$, we have ![]() $\underline{x}_\alpha \lt \bar{x}_\alpha$ and
$\underline{x}_\alpha \lt \bar{x}_\alpha$ and ![]() $x_\alpha \in (\underline{x}_\alpha,\bar{x}_\alpha)$. Combining the above facts, we have the second and the third statements of the lemma.
$x_\alpha \in (\underline{x}_\alpha,\bar{x}_\alpha)$. Combining the above facts, we have the second and the third statements of the lemma.
We now turn to the last statement of the lemma. Note that for ![]() $\alpha \in (0,1/9)$, we have
$\alpha \in (0,1/9)$, we have
 \begin{equation*}g_\alpha(\bar x_\alpha)=\int_{\underline{x}_\alpha}^{\bar x_\alpha}\, \log(f_\alpha(x))\,{\rm dx} \geq \log(f_\alpha(x_\alpha)) =\log(r_\alpha) \gt 0,\end{equation*}
\begin{equation*}g_\alpha(\bar x_\alpha)=\int_{\underline{x}_\alpha}^{\bar x_\alpha}\, \log(f_\alpha(x))\,{\rm dx} \geq \log(f_\alpha(x_\alpha)) =\log(r_\alpha) \gt 0,\end{equation*}where the last inequality follows from the fact that ![]() $r_\alpha=f_\alpha(x_\alpha) \gt 1$ for
$r_\alpha=f_\alpha(x_\alpha) \gt 1$ for ![]() $\alpha \in (0,1/9)$ as established in the previous paragraph. Using Eq. (12), we can compute g α in closed form. This is given as follows:
$\alpha \in (0,1/9)$ as established in the previous paragraph. Using Eq. (12), we can compute g α in closed form. This is given as follows:
 \begin{align}
g_\alpha(x) &=
x\,\log\left(\frac{\left(1-\alpha\right)x}{\alpha+\left(1-\alpha\right)x^2}\right)- \left(1-x\right)\,\log\left(1-x\right)+\log\left(1-\underline{x}_\alpha\right) \nonumber\\
& -2\sqrt{\frac{\alpha}{1-\alpha}}\left(\arctan\left(\sqrt{\frac{1-\alpha}{\alpha}}x\right)-\arctan\left(\sqrt{\frac{1-\alpha}{\alpha}}\underline{x}_\alpha\right)\right).
\end{align}
\begin{align}
g_\alpha(x) &=
x\,\log\left(\frac{\left(1-\alpha\right)x}{\alpha+\left(1-\alpha\right)x^2}\right)- \left(1-x\right)\,\log\left(1-x\right)+\log\left(1-\underline{x}_\alpha\right) \nonumber\\
& -2\sqrt{\frac{\alpha}{1-\alpha}}\left(\arctan\left(\sqrt{\frac{1-\alpha}{\alpha}}x\right)-\arctan\left(\sqrt{\frac{1-\alpha}{\alpha}}\underline{x}_\alpha\right)\right).
\end{align}
From the above, it follows that ![]() $\lim_{x \to 1^{-}} g(x) \lt 0$, since
$\lim_{x \to 1^{-}} g(x) \lt 0$, since ![]() $\underline{x}_\alpha \lt 1$ and
$\underline{x}_\alpha \lt 1$ and ![]() $\arctan(\cdot)$ is an increasing function. Furthermore, we have
$\arctan(\cdot)$ is an increasing function. Furthermore, we have ![]() $g^{\prime}_\alpha(x)=\log(f_\alpha(x)) \lt 0$ for
$g^{\prime}_\alpha(x)=\log(f_\alpha(x)) \lt 0$ for ![]() $x\in (\bar x_\alpha,1)$. Hence, there must exist a unique root
$x\in (\bar x_\alpha,1)$. Hence, there must exist a unique root ![]() $p_c(\alpha)$ of g α in
$p_c(\alpha)$ of g α in ![]() $(\bar x_\alpha, 1)$, and
$(\bar x_\alpha, 1)$, and ![]() $g_\alpha(p)$ must be strictly negative for
$g_\alpha(p)$ must be strictly negative for ![]() $p \in (p_c(\alpha),1)$ and strictly positive for
$p \in (p_c(\alpha),1)$ and strictly positive for ![]() $p \in [\bar{x}_\alpha,p_c(\alpha))$.
$p \in [\bar{x}_\alpha,p_c(\alpha))$.
We are now in a position to complete the proof of Theorem 3.1. We use Lemma 3.4 and the properties of f α proved in Lemma 3.5 to obtain upper bounds of ![]() $\mathbb{E}_{x}\left[\zeta_k\right]$. These upper bounds, in turn, provide upper bounds on
$\mathbb{E}_{x}\left[\zeta_k\right]$. These upper bounds, in turn, provide upper bounds on ![]() $\mathbb{E}_{x}\left[Z_k\right]$ using Eq. (8). Finally, we use Lemma 3.2 and the upper bounds on
$\mathbb{E}_{x}\left[Z_k\right]$ using Eq. (8). Finally, we use Lemma 3.2 and the upper bounds on ![]() $\mathbb{E}_{x}[Z_k]$ to obtain an upper bound on the mean consensus time
$\mathbb{E}_{x}[Z_k]$ to obtain an upper bound on the mean consensus time ![]() $\bar T_n(p)$. The complete proof is given below.
$\bar T_n(p)$. The complete proof is given below.
Proof of Theorem 3.1
From Lemma 3.2, it follows that
 \begin{align}
\bar T_n(p) &=\sum_{k=0}^{n-1} \frac{\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]}{(1-p_{k,k})} \nonumber\\
&= \sum_{k=0}^{n-1} \frac{\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]}{\left(1-\frac{k}{n}\right)\left(\alpha+\left(1-\alpha\right)\frac{k}{n}\right)} \nonumber\\
&=n\sum_{k=0}^{n-1} \mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]\left(\frac{1}{n-k}+\frac{1}{\frac{\alpha}{1-\alpha}n+k}\right).
\end{align}
\begin{align}
\bar T_n(p) &=\sum_{k=0}^{n-1} \frac{\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]}{(1-p_{k,k})} \nonumber\\
&= \sum_{k=0}^{n-1} \frac{\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]}{\left(1-\frac{k}{n}\right)\left(\alpha+\left(1-\alpha\right)\frac{k}{n}\right)} \nonumber\\
&=n\sum_{k=0}^{n-1} \mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]\left(\frac{1}{n-k}+\frac{1}{\frac{\alpha}{1-\alpha}n+k}\right).
\end{align}
Hence, to prove ![]() $T_n(p)=O(n\, \log n)$, it is sufficient to establish that
$T_n(p)=O(n\, \log n)$, it is sufficient to establish that ![]() $\mathbb{E}_{\lceil p n \rceil}\left[Z_k\right] \leq C$ for all
$\mathbb{E}_{\lceil p n \rceil}\left[Z_k\right] \leq C$ for all ![]() $k \in \{0,1,\ldots,n\}$, where C > 0 is a constant independent of k. Indeed, if
$k \in \{0,1,\ldots,n\}$, where C > 0 is a constant independent of k. Indeed, if ![]() $\mathbb{E}_{\lceil p n \rceil}\left[Z_k\right] \leq C$ for each state
$\mathbb{E}_{\lceil p n \rceil}\left[Z_k\right] \leq C$ for each state ![]() $k \in \{0,1,\ldots,n\}$, then for
$k \in \{0,1,\ldots,n\}$, then for  $n \geq \frac{1-\alpha}{\alpha}$, we have
$n \geq \frac{1-\alpha}{\alpha}$, we have
 \begin{align}
\bar T_n(p) & \leq n {C}\sum_{k=0}^{n-1} \left(\frac{1}{n-k}+\frac{1}{k+1}\right) \nonumber \\
&=2 n {C}\sum_{k=1}^{n-1}\frac{1}{k} \nonumber\\
&=O\left(n\,\log n\right).
\end{align}
\begin{align}
\bar T_n(p) & \leq n {C}\sum_{k=0}^{n-1} \left(\frac{1}{n-k}+\frac{1}{k+1}\right) \nonumber \\
&=2 n {C}\sum_{k=1}^{n-1}\frac{1}{k} \nonumber\\
&=O\left(n\,\log n\right).
\end{align}
Hence, to prove the first two statements of the theorem, it is sufficient to show that, under the conditions stated in these statements, ![]() $\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]$ is uniformly bounded by some constant for all
$\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]$ is uniformly bounded by some constant for all ![]() $k \in \left\{0,1,\ldots,n-1\right\}$. This is what we prove next.
$k \in \left\{0,1,\ldots,n-1\right\}$. This is what we prove next.
Using the first two properties of f α proved in Lemma 3.5 and Eq. (9), we see that for ![]() $\alpha \in (1/9,1)$ we have
$\alpha \in (1/9,1)$ we have
 \begin{equation}
\mathbb{E}_{x}\left[\zeta_{k}\right]\leq \begin{cases}
\sum_{t=k}^{n-1} r_\alpha^{t-k+1} \lt \frac{r_\alpha}{1-r_\alpha}, &\quad \text{for } x \leq k \leq n-1,\\
\mathbb{E}_{x}\left[\zeta_{x}\right] \lt \frac{r_\alpha}{1-r_\alpha}, &\quad \text{for } k \lt x,
\end{cases}
\end{equation}
\begin{equation}
\mathbb{E}_{x}\left[\zeta_{k}\right]\leq \begin{cases}
\sum_{t=k}^{n-1} r_\alpha^{t-k+1} \lt \frac{r_\alpha}{1-r_\alpha}, &\quad \text{for } x \leq k \leq n-1,\\
\mathbb{E}_{x}\left[\zeta_{x}\right] \lt \frac{r_\alpha}{1-r_\alpha}, &\quad \text{for } k \lt x,
\end{cases}
\end{equation}
where ![]() $r_\alpha \lt 1$ is as defined in Lemma 3.5. Hence, from Eq. (8), we have that for all
$r_\alpha \lt 1$ is as defined in Lemma 3.5. Hence, from Eq. (8), we have that for all ![]() $\alpha \in (1/9,1)$ and all
$\alpha \in (1/9,1)$ and all ![]() $k \in \left\{0,1,\ldots,n-1\right\}$,
$k \in \left\{0,1,\ldots,n-1\right\}$,
 \begin{equation*}\mathbb{E}_{x}\left[Z_k\right]\leq \frac{1+r_\alpha}{1-r_\alpha}.\end{equation*}
\begin{equation*}\mathbb{E}_{x}\left[Z_k\right]\leq \frac{1+r_\alpha}{1-r_\alpha}.\end{equation*}This establishes the first statement of the theorem.
We now prove the second statement of the theorem. For ![]() $\alpha \in (0,1/9)$, the third statement of Lemma 3.5 implies
$\alpha \in (0,1/9)$, the third statement of Lemma 3.5 implies ![]() $p_c(\alpha) \gt \bar x_\alpha$. Furthermore, by the first and third statements of Lemma 3.5, it follows that f α is strictly decreasing in the range
$p_c(\alpha) \gt \bar x_\alpha$. Furthermore, by the first and third statements of Lemma 3.5, it follows that f α is strictly decreasing in the range ![]() $[\bar x_\alpha,1)$. Hence, for
$[\bar x_\alpha,1)$. Hence, for ![]() $p \geq p_c(\alpha) \gt \bar x_\alpha$, we have
$p \geq p_c(\alpha) \gt \bar x_\alpha$, we have ![]() $f_\alpha(p) \lt f_\alpha(\bar x_\alpha) =1$. Furthermore, for all
$f_\alpha(p) \lt f_\alpha(\bar x_\alpha) =1$. Furthermore, for all ![]() $k \geq x \geq pn$, we have
$k \geq x \geq pn$, we have
 \begin{equation*}\frac{p_{k,k-1}}{p_{k,k+1}}=f_\alpha(k/n)\leq f_\alpha(p) \lt 1.\end{equation*}
\begin{equation*}\frac{p_{k,k-1}}{p_{k,k+1}}=f_\alpha(k/n)\leq f_\alpha(p) \lt 1.\end{equation*} Let ![]() $r_p\triangleq f_\alpha(p) \lt 1$. Then, from Eq. (9), we have that for
$r_p\triangleq f_\alpha(p) \lt 1$. Then, from Eq. (9), we have that for ![]() $k \geq x$
$k \geq x$
 \begin{equation*}\mathbb{E}_{x}\left[\zeta_k\right]\leq \sum_{t=k}^{n-1} r_p^{t-k+1} \lt \frac{r_p}{1-r_p}.\end{equation*}
\begin{equation*}\mathbb{E}_{x}\left[\zeta_k\right]\leq \sum_{t=k}^{n-1} r_p^{t-k+1} \lt \frac{r_p}{1-r_p}.\end{equation*}Hence, from Eq. (8), we have that
 \begin{equation*}\mathbb{E}_{x}\left[Z_k\right] \leq \frac{1+r_p}{1-r_p}\end{equation*}
\begin{equation*}\mathbb{E}_{x}\left[Z_k\right] \leq \frac{1+r_p}{1-r_p}\end{equation*}for ![]() $k \geq x$. Moreover, for
$k \geq x$. Moreover, for ![]() $k\lt n\bar{x}_\alpha \leq x= \lceil pn \rceil$, we have
$k\lt n\bar{x}_\alpha \leq x= \lceil pn \rceil$, we have
 \begin{align*}
\prod_{i=k}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=k}^{\lceil pn \rceil-1} f_\alpha(i/n)\\
& \overset{(a)}{\leq} \prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil pn \rceil-1} f(i/n)\\
&=\exp\left(\sum_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil pn \rceil-1}\log\left(\ f_\alpha(i/n)\right)\right)\\
&{\overset{(b)}{=}\exp\left(n\left( \int_{\underline{x}_\alpha}^{p} \log (f_\alpha(x))\,{\rm d}x +O(1/n)\right)\right)}\\
& \overset{(c)}{=}\exp\left(n {g_\alpha(p)} +O(1)\right)\\
&\overset{(d)}{=}O(1),
\end{align*}
\begin{align*}
\prod_{i=k}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=k}^{\lceil pn \rceil-1} f_\alpha(i/n)\\
& \overset{(a)}{\leq} \prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil pn \rceil-1} f(i/n)\\
&=\exp\left(\sum_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil pn \rceil-1}\log\left(\ f_\alpha(i/n)\right)\right)\\
&{\overset{(b)}{=}\exp\left(n\left( \int_{\underline{x}_\alpha}^{p} \log (f_\alpha(x))\,{\rm d}x +O(1/n)\right)\right)}\\
& \overset{(c)}{=}\exp\left(n {g_\alpha(p)} +O(1)\right)\\
&\overset{(d)}{=}O(1),
\end{align*}
where (a) follows from the facts that ![]() $f_\alpha(i/n) \leq 1$ for
$f_\alpha(i/n) \leq 1$ for ![]() $i \leq n\underline{x}_\alpha$ and
$i \leq n\underline{x}_\alpha$ and ![]() $f_\alpha(i/n) \geq 1$ for
$f_\alpha(i/n) \geq 1$ for ![]() $n\underline{x}_\alpha \leq i \leq n\bar{x}_\alpha$; (b) follows from the fact that the Riemannian sum
$n\underline{x}_\alpha \leq i \leq n\bar{x}_\alpha$; (b) follows from the fact that the Riemannian sum  $(1/n)\sum_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil pn \rceil-1}\log\left(f_\alpha(i/n)\right)$ converges to the integral
$(1/n)\sum_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil pn \rceil-1}\log\left(f_\alpha(i/n)\right)$ converges to the integral  $\int_{\underline{x}_\alpha}^{p} \log (f_\alpha(x))\,{\rm d}x$ as
$\int_{\underline{x}_\alpha}^{p} \log (f_\alpha(x))\,{\rm d}x$ as ![]() $n \to \infty$ with an error of
$n \to \infty$ with an error of ![]() $O(1/n)$; (c) follows from the definition of g α in Lemma 3.5; (d) follows from the fact that for
$O(1/n)$; (c) follows from the definition of g α in Lemma 3.5; (d) follows from the fact that for ![]() $p \geq p_c(\alpha) \gt \bar x_\alpha$, we have
$p \geq p_c(\alpha) \gt \bar x_\alpha$, we have ![]() $g_\alpha(p) \leq 0$ by the last statement of Lemma 3.5. For
$g_\alpha(p) \leq 0$ by the last statement of Lemma 3.5. For ![]() $x \gt k \geq n \bar x_\alpha$, we have
$x \gt k \geq n \bar x_\alpha$, we have
 \begin{align*}
\prod_{i=k}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=k}^{\lceil pn \rceil-1} f(i/n)
\leq 1,
\end{align*}
\begin{align*}
\prod_{i=k}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=k}^{\lceil pn \rceil-1} f(i/n)
\leq 1,
\end{align*}
because for ![]() $i \geq n \bar{x}_\alpha$, we have
$i \geq n \bar{x}_\alpha$, we have ![]() $f_\alpha(i/n) \leq 1$. Hence, for all k < x, it follows from Eq. (9) that
$f_\alpha(i/n) \leq 1$. Hence, for all k < x, it follows from Eq. (9) that ![]() $\mathbb{E}_{x}\left[\zeta_k\right]=O(1) \mathbb{E}_{x}\left[\zeta_x\right]=O(1)$. Finally, from Eq. (8), we obtain that
$\mathbb{E}_{x}\left[\zeta_k\right]=O(1) \mathbb{E}_{x}\left[\zeta_x\right]=O(1)$. Finally, from Eq. (8), we obtain that ![]() $\mathbb{E}_{x}\left[Z_k\right] =O(1)$ for all k < x. This establishes the second statement of the theorem.
$\mathbb{E}_{x}\left[Z_k\right] =O(1)$ for all k < x. This establishes the second statement of the theorem.
We now turn to the third statement of the theorem. Note from Eq. (17) that to prove this statement, it suffices to show that ![]() $\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]=\Omega(\exp(\Theta(n)))$ for
$\mathbb{E}_{\lceil pn \rceil}\left[Z_k\right]=\Omega(\exp(\Theta(n)))$ for ![]() $k =\lceil n\underline{x}_\alpha \rceil$ when
$k =\lceil n\underline{x}_\alpha \rceil$ when ![]() $\alpha \in (0,1/9)$ and
$\alpha \in (0,1/9)$ and ![]() $p \in (0, p_c(\alpha))$. First, note that for
$p \in (0, p_c(\alpha))$. First, note that for ![]() $\alpha \in (0,1/9)$,
$\alpha \in (0,1/9)$, ![]() $p \in (\underline{x}_\alpha,p_c(\alpha))$, and
$p \in (\underline{x}_\alpha,p_c(\alpha))$, and ![]() $k=\lceil n\underline{x}_\alpha \rceil$, we have
$k=\lceil n\underline{x}_\alpha \rceil$, we have
 \begin{align*}
\prod_{i=\lceil n\underline{x}_\alpha \rceil}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil np \rceil-1} f_\alpha(i/n)\\
&=\exp\left(n \int_{\underline{x}_\alpha}^{p}\log(f_\alpha(x))\,{\rm d}x +O(1)\right)\\
&=\Omega(\exp(\Theta(n))),
\end{align*}
\begin{align*}
\prod_{i=\lceil n\underline{x}_\alpha \rceil}^{x-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil np \rceil-1} f_\alpha(i/n)\\
&=\exp\left(n \int_{\underline{x}_\alpha}^{p}\log(f_\alpha(x))\,{\rm d}x +O(1)\right)\\
&=\Omega(\exp(\Theta(n))),
\end{align*}
where the last line follows from the fact that  $\int_{\underline{x}_\alpha}^{p}\log(f_\alpha(x))\,{\rm d}x=g_\alpha(p) \gt 0$ for
$\int_{\underline{x}_\alpha}^{p}\log(f_\alpha(x))\,{\rm d}x=g_\alpha(p) \gt 0$ for ![]() $p\in (\underline{x}_\alpha,p_c(\alpha))$. Hence,
$p\in (\underline{x}_\alpha,p_c(\alpha))$. Hence,  $\mathbb{E}_{x}\left[\zeta_{\lceil \underline{x}_\alpha n \rceil}\right]=\Omega(\exp(\Theta(n)))\mathbb{E}_{x}\left[\zeta_x\right]
=f_\alpha(p)\Omega(\exp(\Theta(n)))$, since
$\mathbb{E}_{x}\left[\zeta_{\lceil \underline{x}_\alpha n \rceil}\right]=\Omega(\exp(\Theta(n)))\mathbb{E}_{x}\left[\zeta_x\right]
=f_\alpha(p)\Omega(\exp(\Theta(n)))$, since ![]() $\mathbb{E}_{x}\left[\zeta_x\right] \gt f_\alpha(x/n)=f_\alpha(p)+o(1)$. Hence,
$\mathbb{E}_{x}\left[\zeta_x\right] \gt f_\alpha(x/n)=f_\alpha(p)+o(1)$. Hence,  $\mathbb{E}_{x}\left[Z_{\lceil n\underline{x}_\alpha \rceil}\right]=\Omega(\exp(\Theta(n)))$. For
$\mathbb{E}_{x}\left[Z_{\lceil n\underline{x}_\alpha \rceil}\right]=\Omega(\exp(\Theta(n)))$. For ![]() $p \in [0,\underline{x}_\alpha]$, we have
$p \in [0,\underline{x}_\alpha]$, we have
 \begin{align*}
\mathbb{E}_{x}\left[\zeta_{\lceil \underline{x}_\alpha n \rceil}\right]\gt \prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil n\bar{x}_\alpha \rceil-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil n\bar{x}_\alpha \rceil-1} f_\alpha(i/n)\\
&=\exp\left(n \int_{\underline{x}_\alpha}^{\bar{x}_\alpha}\log(f_\alpha(x))\,{\rm d}x +O(1)\right)\\
&=\Omega(\exp(\Theta(n))).
\end{align*}
\begin{align*}
\mathbb{E}_{x}\left[\zeta_{\lceil \underline{x}_\alpha n \rceil}\right]\gt \prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil n\bar{x}_\alpha \rceil-1} \frac{p_{i,i-1}}{p_{i,i+1}}
&=\prod_{i=\lceil n\underline{x}_\alpha \rceil}^{\lceil n\bar{x}_\alpha \rceil-1} f_\alpha(i/n)\\
&=\exp\left(n \int_{\underline{x}_\alpha}^{\bar{x}_\alpha}\log(f_\alpha(x))\,{\rm d}x +O(1)\right)\\
&=\Omega(\exp(\Theta(n))).
\end{align*}
This proves the third part of the theorem.
Remark 3.6. From the proof above, it is clear that the absorption time of the chain ![]() $\bar Y^n$ crucially depends on the ratio of the down-transition probability
$\bar Y^n$ crucially depends on the ratio of the down-transition probability ![]() $p_{i,i-1}$ to the up-transition probability
$p_{i,i-1}$ to the up-transition probability ![]() $p_{i,i+1}$ at any given state i. If this ratio is smaller than one at a given state i, then the chain has a tendency to drift quickly toward the absorbing state n. Similarly, if the ratio is larger than one, then the chain has a tendency to move toward state 0, and hence it takes longer to reach the absorbing state n. Since the value of this ratio depends on the bias parameter α as well as on the initial proportion p of agents with the superior opinion, we observe phase transitions with respect to both the parameters.
$p_{i,i+1}$ at any given state i. If this ratio is smaller than one at a given state i, then the chain has a tendency to drift quickly toward the absorbing state n. Similarly, if the ratio is larger than one, then the chain has a tendency to move toward state 0, and hence it takes longer to reach the absorbing state n. Since the value of this ratio depends on the bias parameter α as well as on the initial proportion p of agents with the superior opinion, we observe phase transitions with respect to both the parameters.
Remark 3.7. Although we have proved the theorem for the modified chain ![]() $\bar{Y}^n$, the proof can be extended to the original chain
$\bar{Y}^n$, the proof can be extended to the original chain ![]() $\bar X^n$. This is because the results of Lemma 3.2 and Lemma 3.4 are also applicable to the original chain if the transition probabilities are replaced by those of the original chain. Furthermore, the transition probabilities of the two chains satisfy the following relations:
$\bar X^n$. This is because the results of Lemma 3.2 and Lemma 3.4 are also applicable to the original chain if the transition probabilities are replaced by those of the original chain. Furthermore, the transition probabilities of the two chains satisfy the following relations:
 \begin{equation*}1-\tilde{p}_{k,k}=1-p_{k,k}+\left(1-\alpha\right)\frac{k}{n}\left(1-\frac{k}{n}\right)\left(\frac{n^2}{\left(n-1\right)^2}-1\right)\leq 1-p_{k,k},\end{equation*}
\begin{equation*}1-\tilde{p}_{k,k}=1-p_{k,k}+\left(1-\alpha\right)\frac{k}{n}\left(1-\frac{k}{n}\right)\left(\frac{n^2}{\left(n-1\right)^2}-1\right)\leq 1-p_{k,k},\end{equation*}and ![]() $\tilde{p}_{k,k-1}/\tilde{p}_{k,k+1}={p_{k,k-1}}/{p_{k,k+1}}+o(1)$, where we recall that
$\tilde{p}_{k,k-1}/\tilde{p}_{k,k+1}={p_{k,k-1}}/{p_{k,k+1}}+o(1)$, where we recall that ![]() $\tilde{p}_{k,k}$ denotes the transition probability from state k to itself for the original chain
$\tilde{p}_{k,k}$ denotes the transition probability from state k to itself for the original chain ![]() $\bar X^n$. We note that the same lower bound as in Lemma 3.3 can be obtained for the chain
$\bar X^n$. We note that the same lower bound as in Lemma 3.3 can be obtained for the chain ![]() $\bar X^n$ since we have
$\bar X^n$ since we have ![]() $1-\tilde{p}_{k,k} \leq (\max(\alpha,1-\alpha)+o(1))(1-k/n)(1+k/n)$. Similarly, the upper and lower bounds on the expected number of visits to each state derived for the modified chain also hold for the original chain for large enough n. Combining the above, we obtain the same asymptotic bounds for the original chain
$1-\tilde{p}_{k,k} \leq (\max(\alpha,1-\alpha)+o(1))(1-k/n)(1+k/n)$. Similarly, the upper and lower bounds on the expected number of visits to each state derived for the modified chain also hold for the original chain for large enough n. Combining the above, we obtain the same asymptotic bounds for the original chain ![]() $\bar X^n$ as we have for the modified chain
$\bar X^n$ as we have for the modified chain ![]() $\bar Y^n$.
$\bar Y^n$.
4. Numerical Results
In this section, we present numerical results for the model presented in this paper. We first present results to support our theoretical findings on complete graphs. We then present simulation results for other classes of graphs. Error bars in the plots represent ![]() $95\%$ confidence intervals. Also, to understand the growth rates better, we overlay the plots obtained from simulations on theoretical growth rates obtained by plotting appropriately scaled functions.
$95\%$ confidence intervals. Also, to understand the growth rates better, we overlay the plots obtained from simulations on theoretical growth rates obtained by plotting appropriately scaled functions.
4.1. Complete graphs
For complete graphs, the mean consensus time ![]() $\bar T_n(p)$ can be computed numerically using the first step analysis of the Markov chain
$\bar T_n(p)$ can be computed numerically using the first step analysis of the Markov chain ![]() $\bar Y^n$. This method is more exact and computationally less expensive than simulating the chain a large number of times to obtain the average absorption time. Hence, we adopt this method for complete graphs. With a slight abuse of notation, let
$\bar Y^n$. This method is more exact and computationally less expensive than simulating the chain a large number of times to obtain the average absorption time. Hence, we adopt this method for complete graphs. With a slight abuse of notation, let ![]() $\bar T_n(k)$ denote the average absorption time of the chain starting from state
$\bar T_n(k)$ denote the average absorption time of the chain starting from state ![]() $k \in \left\{0,1,\ldots,n\right\}$. Then, from first step analysis, we have for each
$k \in \left\{0,1,\ldots,n\right\}$. Then, from first step analysis, we have for each ![]() $k \in \left\{0,1,\ldots,n\right\}$,
$k \in \left\{0,1,\ldots,n\right\}$,
where ![]() $p_{i,j}$ is as defined in Eq. (2). Simplifying the above and using the boundary condition
$p_{i,j}$ is as defined in Eq. (2). Simplifying the above and using the boundary condition ![]() $\bar T_n(n)=0$, we obtain
$\bar T_n(n)=0$, we obtain
 \begin{equation}
\bar{T}_n(p):= \bar T_n\left(\lceil np \rceil\right)=\sum_{k=\lceil np \rceil}^{n-1}S_n(k),
\end{equation}
\begin{equation}
\bar{T}_n(p):= \bar T_n\left(\lceil np \rceil\right)=\sum_{k=\lceil np \rceil}^{n-1}S_n(k),
\end{equation}
where ![]() $S_n(k)$ satisfies the following recursion:
$S_n(k)$ satisfies the following recursion:
 \begin{equation}
S_n(k)=\frac{1}{p_{k,k+1}}+\frac{p_{k,k-1}}{p_{k,k+1}}S_n(k-1),
\end{equation}
\begin{equation}
S_n(k)=\frac{1}{p_{k,k+1}}+\frac{p_{k,k-1}}{p_{k,k+1}}S_n(k-1),
\end{equation}
with ![]() $S_n(0)=1/\alpha$. We find the expected consensus time numerically by solving the above recursion for different values of n,
$S_n(0)=1/\alpha$. We find the expected consensus time numerically by solving the above recursion for different values of n, ![]() $\alpha,$ and p. First, we choose
$\alpha,$ and p. First, we choose ![]() $\alpha=0.1 \lt 1/9$. For this value of α, we can numerically compute the value of
$\alpha=0.1 \lt 1/9$. For this value of α, we can numerically compute the value of ![]() $p_c(\alpha)$ by solving Eq. (3). This value turns out to be 0.431 (accurate to the third decimal place). In Figure 1(a) and (b), we plot the normalized (by the network size) average consensus time as a function of the network size for
$p_c(\alpha)$ by solving Eq. (3). This value turns out to be 0.431 (accurate to the third decimal place). In Figure 1(a) and (b), we plot the normalized (by the network size) average consensus time as a function of the network size for ![]() $p=0.4 \lt p_c(\alpha)=0.431$ and
$p=0.4 \lt p_c(\alpha)=0.431$ and ![]() $p=0.5 \gt p_c(\alpha)=0.431$, respectively. As expected from Theorem 3.1, we observe that the mean consensus time grows exponentially for
$p=0.5 \gt p_c(\alpha)=0.431$, respectively. As expected from Theorem 3.1, we observe that the mean consensus time grows exponentially for ![]() $p \lt p_c(\alpha)$ and as
$p \lt p_c(\alpha)$ and as ![]() $\Theta(n \log n)$ for
$\Theta(n \log n)$ for ![]() $p \gt p_c(\alpha)$.
$p \gt p_c(\alpha)$.

Figure 1. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for
$\bar{T}_n(p)/n$ as a function of the network size for ![]() $\alpha=0.1 \lt 1/9$ for complete graphs. (a)
$\alpha=0.1 \lt 1/9$ for complete graphs. (a) ![]() $\alpha=0.1 \lt 1/9, p=0.4 \lt p_c(\alpha)=0.431$. (b)
$\alpha=0.1 \lt 1/9, p=0.4 \lt p_c(\alpha)=0.431$. (b) ![]() $\alpha=0.1 \lt 1/9, p=0.5 \gt p_c(\alpha)=0.431$.
$\alpha=0.1 \lt 1/9, p=0.5 \gt p_c(\alpha)=0.431$.
Next, we choose ![]() $\alpha =0.125 \gt 1/9$. For this choice of α, we expect (from Theorem 3.1) the mean consensus time to grow as
$\alpha =0.125 \gt 1/9$. For this choice of α, we expect (from Theorem 3.1) the mean consensus time to grow as ![]() $\Theta(n \,\log n)$ for all values of p. This is verified in Figure 2(a) and (b), where we choose p = 0 and p = 0.5, respectively. We observe that in both cases
$\Theta(n \,\log n)$ for all values of p. This is verified in Figure 2(a) and (b), where we choose p = 0 and p = 0.5, respectively. We observe that in both cases ![]() $\bar{T}_n(p)=\Theta(n\, \log n)$.
$\bar{T}_n(p)=\Theta(n\, \log n)$.

Figure 2. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for
$\bar{T}_n(p)/n$ as a function of the network size for ![]() $\alpha=0.125 \gt 1/9$ for complete graphs. (a)
$\alpha=0.125 \gt 1/9$ for complete graphs. (a)![]() $\alpha=0.125 \gt 1/9, p=0$. (b)
$\alpha=0.125 \gt 1/9, p=0$. (b) ![]() $\alpha=0.125 \gt 1/9, p=0.5$.
$\alpha=0.125 \gt 1/9, p=0.5$.
4.2. Random d-regular graphs with  $d=\Theta(\log n)$
$d=\Theta(\log n)$
We now present simulation results for random d-regular graphs where the degree d for each node is chosen to be ![]() $d=\lceil \log n \rceil$. We use the
$d=\lceil \log n \rceil$. We use the ![]() $\texttt{networkx}$ package to generate random d-regular graphs. For each randomly generated graph, we run the protocol until the network reaches consensus. The above procedure is repeated 500 times, and the mean consensus time is computed over these 500 runs. We further repeat this for different values of n, α, and p. In Figure 3(a) and (b), we fix α to be 0.05 and plot the normalized mean consensus time as a function of the network size for p = 0.05 and p = 0.8, respectively. Similar to complete graphs, we observe that the mean consensus time grows exponentially with n when both α and p are low. In contrast, when the initial proportion of agents having the superior opinion is sufficiently large, the mean consensus time grows as
$\texttt{networkx}$ package to generate random d-regular graphs. For each randomly generated graph, we run the protocol until the network reaches consensus. The above procedure is repeated 500 times, and the mean consensus time is computed over these 500 runs. We further repeat this for different values of n, α, and p. In Figure 3(a) and (b), we fix α to be 0.05 and plot the normalized mean consensus time as a function of the network size for p = 0.05 and p = 0.8, respectively. Similar to complete graphs, we observe that the mean consensus time grows exponentially with n when both α and p are low. In contrast, when the initial proportion of agents having the superior opinion is sufficiently large, the mean consensus time grows as ![]() $\Theta(n\,\log n)$ even when the bias parameter α is small.
$\Theta(n\,\log n)$ even when the bias parameter α is small.

Figure 3. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for α = 0.05 for random d-regular graphs with
$\bar{T}_n(p)/n$ as a function of the network size for α = 0.05 for random d-regular graphs with ![]() $d=\lceil \log n \rceil$. (a)
$d=\lceil \log n \rceil$. (a) ![]() $\alpha=0.05, p=0.05$. (b)
$\alpha=0.05, p=0.05$. (b) ![]() $\alpha=0.05, p=0.8$.
$\alpha=0.05, p=0.8$.
In Figure 4(a) and (b), we choose α = 0.8 and plot the normalized mean consensus time as a function of the network size for p = 0.005 and p = 0.8, respectively. We observe that in both cases, the mean consensus time grows as ![]() $\Theta(n\, \log n)$. This indicates that if the bias parameter α is sufficiently large, then the network reaches consensus to the superior opinion in
$\Theta(n\, \log n)$. This indicates that if the bias parameter α is sufficiently large, then the network reaches consensus to the superior opinion in ![]() $\Theta(n \,\log n)$ time irrespective of the initial proportion of agents having the superior opinion.
$\Theta(n \,\log n)$ time irrespective of the initial proportion of agents having the superior opinion.

Figure 4. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for α = 0.8 for random d-regular graphs with
$\bar{T}_n(p)/n$ as a function of the network size for α = 0.8 for random d-regular graphs with ![]() $d=\lceil \log n \rceil$. (a)
$d=\lceil \log n \rceil$. (a) ![]() $\alpha=0.8, p=0.05$. (b)
$\alpha=0.8, p=0.05$. (b) ![]() $\alpha=0.8, p=0.8$.
$\alpha=0.8, p=0.8$.
4.3. Random d-regular graphs with  $d=O(1)$
$d=O(1)$
We now investigate the biased opinion dynamics on random d-regular with constant degree, that is, ![]() $d=O(1)$. Specifically, we set d = 5 and simulate the network for different values of n,
$d=O(1)$. Specifically, we set d = 5 and simulate the network for different values of n, ![]() $\alpha,$ and p. As before, we generate a random 5-regular graph using the networkx package and run the protocol on this randomly generated instance until consensus is reached. The above procedure is repeated multiple times (each with a newly generated random graph) to obtain the mean consensus time within the desired confidence bounds. In Figure 5(a) and (b), we fix α = 0.05 and choose p = 0.05 and p = 0.8, respectively. We observe that the normalized mean consensus time grows approximately linearly in n (i.e.,
$\alpha,$ and p. As before, we generate a random 5-regular graph using the networkx package and run the protocol on this randomly generated instance until consensus is reached. The above procedure is repeated multiple times (each with a newly generated random graph) to obtain the mean consensus time within the desired confidence bounds. In Figure 5(a) and (b), we fix α = 0.05 and choose p = 0.05 and p = 0.8, respectively. We observe that the normalized mean consensus time grows approximately linearly in n (i.e., ![]() $\bar T_n(p)= O(n^2)$) when both α and p are small. This is unlike the previous results for dense graphs, where, for small values of α and p, the mean consensus time is exponential in n. This reduction in absorption time can be intuitively explained by the fact that a smaller neighborhood size reduces the chance of an agent updating to the worse opinion when a fixed proportion of all the agents has the worse opinion. Based on this intuition, we conjecture that for small values of p and α, the mean consensus time grows polynomially in n when the neighborhood size d is a constant higher than 2. The case of cycles (where d = 2) has already been considered in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2]. But in the case of cycles, there is no phase transition; indeed, it has been shown in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2] that for cycles, consensus is achieved on the superior opinion in
$\bar T_n(p)= O(n^2)$) when both α and p are small. This is unlike the previous results for dense graphs, where, for small values of α and p, the mean consensus time is exponential in n. This reduction in absorption time can be intuitively explained by the fact that a smaller neighborhood size reduces the chance of an agent updating to the worse opinion when a fixed proportion of all the agents has the worse opinion. Based on this intuition, we conjecture that for small values of p and α, the mean consensus time grows polynomially in n when the neighborhood size d is a constant higher than 2. The case of cycles (where d = 2) has already been considered in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2]. But in the case of cycles, there is no phase transition; indeed, it has been shown in [Reference Anagnostopoulos, Becchetti, Cruciani, Pasquale and Rizzo2] that for cycles, consensus is achieved on the superior opinion in ![]() $O(n\,\log n)$ time for all values of α even when p = 0.
$O(n\,\log n)$ time for all values of α even when p = 0.

Figure 5. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for α = 0.05 for random d-regular graphs with d = 5. (a)
$\bar{T}_n(p)/n$ as a function of the network size for α = 0.05 for random d-regular graphs with d = 5. (a) ![]() $\alpha=0.05, p=0.05$. (b)
$\alpha=0.05, p=0.05$. (b) ![]() $\alpha=0.05, p=0.8$.
$\alpha=0.05, p=0.8$.

Figure 6. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for α = 0.8 for random d-regular graphs with d = 5. (a)
$\bar{T}_n(p)/n$ as a function of the network size for α = 0.8 for random d-regular graphs with d = 5. (a) ![]() $\alpha=0.8, p=0.05$. (b)
$\alpha=0.8, p=0.05$. (b) ![]() $\alpha=0.8, p=0.8$.
$\alpha=0.8, p=0.8$.
In Figure 6(a) and (b), we plot the mean consensus time as a function of the network size for p = 0.05 and p = 0.8, respectively, keeping α = 0.8. In both cases, we observe that the mean consensus time grows as ![]() $\Theta(n\, \log n)$. Thus, in these regimes, the behavior of random d-regular graphs with
$\Theta(n\, \log n)$. Thus, in these regimes, the behavior of random d-regular graphs with ![]() $d=O(1)$ is similar to that of random d-regular graphs with
$d=O(1)$ is similar to that of random d-regular graphs with ![]() $d=\Theta(\log n)$.
$d=\Theta(\log n)$.
4.4. Erdős–Rényi graphs with edge probability  $\log n/n$
$\log n/n$
Finally, we present results for Erdős–Rényi graphs where the edge probability is fixed at the connectivity threshold ![]() $\log n/n$. The experiments are designed in the same way as described for other classes of graphs. The normalized mean consensus time as a function of the network size n is plotted for different values of α and p: in Figure 7(a) and (b) for α = 0.05 and in Figure 8(a) and (b) for α = 0.8. We observe similar phase transitions as in the case of complete graphs, that is, the mean consensus time grows as
$\log n/n$. The experiments are designed in the same way as described for other classes of graphs. The normalized mean consensus time as a function of the network size n is plotted for different values of α and p: in Figure 7(a) and (b) for α = 0.05 and in Figure 8(a) and (b) for α = 0.8. We observe similar phase transitions as in the case of complete graphs, that is, the mean consensus time grows as ![]() $\Theta(n\log n)$ in all cases except when both α and p are low.
$\Theta(n\log n)$ in all cases except when both α and p are low.

Figure 7. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for α = 0.05 for Erdős–Rényi graphs with edge probability
$\bar{T}_n(p)/n$ as a function of the network size for α = 0.05 for Erdős–Rényi graphs with edge probability ![]() $\log n/n$. (a)
$\log n/n$. (a) ![]() $\alpha=0.05, p=0.05$. (b)
$\alpha=0.05, p=0.05$. (b) ![]() $\alpha=0.05, p=0.8$.
$\alpha=0.05, p=0.8$.

Figure 8. Mean consensus time per node ![]() $\bar{T}_n(p)/n$ as a function of the network size for α = 0.8 for Erdős–Rényi graphs with edge probability
$\bar{T}_n(p)/n$ as a function of the network size for α = 0.8 for Erdős–Rényi graphs with edge probability ![]() $\log n/n$. (a)
$\log n/n$. (a) ![]() $\alpha=0.8, p=0.05$. (b)
$\alpha=0.8, p=0.05$. (b) ![]() $\alpha=0.8, p=0.8$.
$\alpha=0.8, p=0.8$.
5. Conclusion and future work
In this paper, we have studied a model of binary opinion dynamics where the agents show a strong form of bias toward one of the opinions, called the superior opinion. We showed that for complete graphs, the model exhibits rich phase transitions based on the values of the bias parameter and the initial proportion of agents with the superior opinion. Specifically, we proved that fast consensus can be achieved on the superior opinion irrespective of the initial configuration of the network when bias is sufficiently high. When bias is low, we show that fast consensus can only be achieved when the initial proportion of agents with the superior opinion is above a certain threshold. If this is not the case, then we show that consensus takes exponentially long time. Through simulations, we observed similar behavior for several classes of dense graphs where the average degree scales at least logarithmically with the network size. For sparse graphs, where the average degree is constant, we observed that phase transitions do occur but the behavior below criticality is different to that of dense graphs. Specifically, we observed that when both bias and the initial proportion of agents with the superior opinion are low, the average consensus time is still polynomial in the network size.
Several directions remain open for theoretical investigation. One immediate problem is to theoretically establish the observed phase transitions for dense graphs. Here, it will be interesting to find out how “dense” a graph must be in order for it to exhibit the same phase transitions as in complete graphs. Similar questions remain open for sparse graphs such as d-regular expanders with constant d. Here, it will be of interest to find out how the threshold valued of the parameters depend on the average degree d or the spectral properties of the expander. It is also worth analyzing the exact behavior below criticality. The numerical experiments conducted in this paper suggests that the consensus time is still polynomial below criticality (unlike in complete graphs where it is exponential), but it would be challenging to obtain exact bounds in this case.