Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-28T05:46:39.348Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SHIMURA CURVE OF DISCRIMINANT 15 AND TOPOLOGICAL AUTOMORPHIC FORMS

Part of: Homotopy theory Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  05 February 2015

TYLER LAWSON
TYLER LAWSON*
Affiliation:
Department of Mathematics, University of Minnesota, 206 Church Street SE, Minneapolis, MN 55414, USA; tlawson@math.umn.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We find defining equations for the Shimura curve of discriminant 15 over 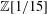$\mathbb{Z}[1/15]$. We then determine the graded ring of automorphic forms over the 2-adic integers, as well as the higher cohomology. We apply this to calculate the homotopy groups of a spectrum of ‘topological automorphic forms’ associated to this curve, as well as one associated to a quotient by an Atkin–Lehner involution.

MSC classification

Primary: 55P42: Stable homotopy theory, spectra
Secondary: 11F23: Relations with algebraic geometry and topology 11G18: Arithmetic aspects of modular and Shimura varieties 14G35: Modular and Shimura varieties 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e3
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Alsina, M. and Bayer, P., ‘Quaternion orders, quadratic forms, and Shimura curves’, in: CRM Monograph Series, Vol. 22 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Behrens, M. and Lawson, T., ‘Topological automorphic forms’, Mem. Amer. Math. Soc. 204(958) (2010), xxiv+141.Google Scholar
Eichler, M., ‘Über die Idealklassenzahl hyperkomplexer Systeme’, Math. Z. 43(1) (1938), 481–494.Google Scholar
Elkies, N. D., ‘Shimura curve computations’, in: Algorithmic Number Theory, Portland, OR, 1998, Lecture Notes in Computer Science, 1423 (Springer, Berlin, 1998), 1–47.Google Scholar
Goerss, P. G., ‘Realizing families of Landweber exact homology theories’, in: New Topological Contexts for Galois Theory and Algebraic Geometry (BIRS 2008), Geom. Topol. Monogr., 16 (Geom. Topol. Publ., Coventry, 2009), 49–78.Google Scholar
Hill, M. and Lawson, T., ‘Automorphic forms and cohomology theories on Shimura curves of small discriminant’, Adv. Math. 225(2) (2010), 1013–1045.Google Scholar
Kudla, S. S., Rapoport, M. and Yang, T., ‘Modular forms and special cycles on Shimura curves’, in: Annals of Mathematics Studies, Vol. 161 (Princeton University Press, Princeton, NJ, 2006).Google Scholar
Kurihara, A., ‘On some examples of equations defining Shimura curves and the Mumford uniformization’, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 25(3) (1979), 277–300.Google Scholar
Landweber, P. S., ‘Homological properties of comodules over MU∗(MU) and BP ∗(BP)’, Amer. J. Math. 98(3) (1976), 591–610.Google Scholar
Michon, J.-F., ‘Courbes de Shimura hyperelliptiques’, Bull. Soc. Math. France 109(2) (1981), 217–225.Google Scholar
Miyake, T., Modular Forms, (Springer, Berlin, 1989), (translated from the Japanese by Y. Maeda).Google Scholar
Morita, Y., ‘Reduction modulo P of Shimura curves’, Hokkaido Math. J. 10(2) (1981), 209–238.Google Scholar
Mahowald, M. and Rezk, C., ‘Topological modular forms of level 3’, Pure Appl. Math. Q. 5(2) (2009), 853–872. (special issue: in honor of Friedrich Hirzebruch. Part 1).Google Scholar
Quillen, D., ‘On the formal group laws of unoriented and complex cobordism theory’, Bull. Amer. Math. Soc. 75 (1969), 1293–1298.Google Scholar
Vignéras, M.-F., Arithmétique des algèbres de quaternions, Lecture Notes in Mathematics, 800 (Springer, Berlin, 1980).Google Scholar