Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-28T18:33:35.834Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTRIBUTION OF FROBENIUS ELEMENTS IN FAMILIES OF GALOIS EXTENSIONS

Published online by Cambridge University Press:  19 May 2023

Daniel Fiorilli Open the ORCID record for Daniel Fiorilli [Opens in a new window]  and
Florent Jouve Open the ORCID record for Florent Jouve [Opens in a new window]
Daniel Fiorilli
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire de Mathématiques d’Orsay, 91405, Orsay, France (daniel.fiorilli@universite-paris-saclay.fr)
Florent Jouve*
Affiliation:
Université de Bordeaux, CNRS, Bordeaux INP, IMB, UMR 5251, F-33400, Talence, France
*
florent.jouve@math.u-bordeaux.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a Galois extension $L/K$ of number fields, we describe fine distribution properties of Frobenius elements via invariants from representations of finite Galois groups and ramification theory. We exhibit explicit families of extensions in which we evaluate these invariants and deduce a detailed understanding and a precise description of the possible asymmetries. We establish a general bound on the generic fluctuations of the error term in the Chebotarev density theorem, which under GRH is sharper than the Murty–Murty–Saradha and Bellaïche refinements of the Lagarias–Odlyzko and Serre bounds, and which we believe is best possible (assuming simplicity, it is of the quality of Montgomery’s conjecture on primes in arithmetic progressions). Under GRH and a hypothesis on the multiplicities of zeros up to a certain height, we show that in certain families, these fluctuations are dominated by a constant lower order term. As an application of our ideas, we refine and generalize results of K. Murty and of Bellaïche, and we answer a question of Ng. In particular, in the case where 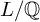$L/{\mathbb {Q}}$ is Galois and supersolvable, we prove a strong form of a conjecture of K. Murty on the unramified prime ideal of least norm in a given Frobenius set. The tools we use include the Rubinstein–Sarnak machinery based on limiting distributions and a blend of algebraic, analytic, representation theoretic, probabilistic and combinatorial techniques.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 3 , May 2024 , pp. 1169 - 1258
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

References

Akbary, A., Ng, N. and Shahabi, M., Limiting distributions of the classical error terms of prime number theory, Q. J. Math. 65(3) (2014), 743–780.10.1093/qmath/hat059CrossRefGoogle Scholar
Andrews, G. E., The theory of partitions, in Encyclopedia of Mathematics and its Applications, Vol. 2, pp. xiv+255 (Addison-Wesley Publishing Co., Reading, Mass.-London-Amsterdam, 1976).Google Scholar
Armitage, J. V., Zeta functions with a zero at $s=\frac{1}{2}$ , Invent. Math. 15 (1972), 199–205.10.1007/BF01404125CrossRefGoogle Scholar
Bailleul, A., Chebyshev’s bias in dihedral and generalized quaternion Galois groups, Algebra Number Theory 15(4) (2021), 999–1041.10.2140/ant.2021.15.999CrossRefGoogle Scholar
Bailleul, A., Explicit Kronecker-Weyl theorems and applications to prime number race, Res. Number Theory 8(3) (2022), Paper No. 43. https://doi.org/10.1007/s40993-022-00349-2 CrossRefGoogle Scholar
Bellaïche, J., Théorème de Chebotarev et complexité de Littlewood, Ann. Sci. Éc. Norm. Supér. 49 (2016), 579–632.10.24033/asens.2291CrossRefGoogle Scholar
Bellaïche, J., Remarks on the error term in Chebotarev’s density theorem, Math. Res. Lett. 24(3) (2017), 679–687.10.4310/MRL.2017.v24.n3.a4CrossRefGoogle Scholar
Best, D. G. and Trudgian, T. S., Linear relations of zeroes of the zeta-function, Math. Comp. 84(294) (2015), 2047–2058.10.1090/S0025-5718-2014-02916-5CrossRefGoogle Scholar
Boston, N. and Markin, N., The fewest primes ramified in a $G$ -extension of $\mathbb{Q}$ , Ann. Sci. Math. Québec 33(2) (2009), 145–154.Google Scholar
Bourgain, J., A remark on solutions of the Pell equation, Int. Math. Res. Not. IMRN (2014). https://doi.org/10.1093/imrn/rnu023 CrossRefGoogle Scholar
de la Bretèche, R., Kurlberg, P. and Shparlinski, I., On the number of products which form perfect powers and discriminants of multiquadratic extensions, Int. Math. Res. Not. IMRN (2021). https://doi.org/10.48550/arXiv.1901.10694 CrossRefGoogle Scholar
Brueggeman, S. and Doud, D., Local corrections of discriminant bounds and small degree extensions of quadratic base fields, Int. J. Number Theory 4(3) (2008), 349–361.10.1142/S1793042108001389CrossRefGoogle Scholar
Bucur, A. and Kedlaya, K., An application of the effective Sato–Tate conjecture, in Frobenius distributions: Lang–Trotter and Sato–Tate conjectures, Contemporary Mathematics, vol. 663, pp. 45–56 (American Mathematical Society, Providence, RI, 2016).10.1090/conm/663/13349CrossRefGoogle Scholar
Cha, B., Chebyshev’s bias in function fields, Compos. Math. 144(6) (2008), 1351–1374.10.1112/S0010437X08003631CrossRefGoogle Scholar
Cha, B. and Im, B.-H., Chebyshev’s bias in Galois extensions of global function fields, J. Number Theory 131(10) (2011), 1875–1886.10.1016/j.jnt.2011.03.011CrossRefGoogle Scholar
Cha, B., Fiorilli, D. and Jouve, F., Prime number races for elliptic curves over function fields, Ann. Sci. Éc. Norm. Supér. (2016). https://doi.org/10.48550/arXiv.1502.05295 CrossRefGoogle Scholar
Cho, P. J. and Kim, H. H., Effective prime ideal theorem and exponents of ideal class groups, Q. J. Math. 65(4) (2014), 1179–1193.10.1093/qmath/hau002CrossRefGoogle Scholar
Cho, P. J. and Kim, H. H., The average of the smallest prime in a conjugacy class, Int. Math. Res. Not. IMRN (2020). https://doi.org/10.48550/arXiv.1601.03012 CrossRefGoogle Scholar
Chowla, S., On the class-number of the corpus $P\left(\sqrt{-k}\right)$ , Proc. Nat. Inst. Sci. India 13 (1947), 197–200.Google Scholar
Devin, L., Chebyshev’s bias for analytic $L$ -functions, Math. Proc. Cambridge Philos. Soc. 169(1) (2020), 103–140.10.1017/S0305004119000100CrossRefGoogle Scholar
Devin, L. and Meng, X., Chebyshev’s bias for products of irreducible polynomials, Adv. Math. 392 (2021), Paper No. 108040, 45 pp. https://doi.org/10.48550/arXiv.1809.09662 CrossRefGoogle Scholar
Dietmann, R., Probabilistic Galois theory, Bull. Lond. Math. Soc. 45(3) (2013), 453–462.10.1112/blms/bds113CrossRefGoogle Scholar
Dummit, D., Granville, A. and Kisilevsky, H., Big biases amongst products of two primes, Mathematika 62(2) (2016), 502–507.10.1112/S0025579315000339CrossRefGoogle Scholar
Duke, W., Number fields with large class group, in Number theory, CRM Proceedings & Lecture Notes, vol. 36, pp. 117–126 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Esseen, C.-G., Fourier analysis of distribution functions. A mathematical study of the Laplace-Gaussian law. Acta Math. 77 (1945), 1–125.10.1007/BF02392223CrossRefGoogle Scholar
Euvrard, C. and Maire, C., Sur la séparation des caractères par les Frobenius, Publ. Mat. 61(2) (2017), 475–515.10.5565/PUBLMAT6121706CrossRefGoogle Scholar
Féray, V. and Śniady, P., Asymptotics of characters of symmetric groups related to Stanley character formula, Ann. of Math. (2) 173(2) (2011), 887–906.10.4007/annals.2011.173.2.6CrossRefGoogle Scholar
Fiori, A., Lower bounds for the least prime in Chebotarev, Algebra Number Theory 13(9) (2019), 2199–2203.10.2140/ant.2019.13.2199CrossRefGoogle Scholar
Fiorilli, D., Highly biased prime number races, Algebra Number Theory 8(7) (2014), 1733–1767.10.2140/ant.2014.8.1733CrossRefGoogle Scholar
Fiorilli, D., Elliptic curves of unbounded rank and Chebyshev’s bias, Int. Math. Res. Not. IMRN 2014(18) (2014), 4997–5024.10.1093/imrn/rnt103CrossRefGoogle Scholar
Fiorilli, D. and Martin, G., Inequities in the Shanks-Rényi prime number race: An asymptotic formula for the densities, J. Reine Angew. Math. 676 (2013), 121–212.Google Scholar
Ford, K. and Sneed, J., Chebyshev’s bias for products of two primes, Experiment. Math. 19(4) (2010), 385–398.10.1080/10586458.2010.10390630CrossRefGoogle Scholar
Fouvry, É., On the size of the fundamental solution of the Pell equation, J. Reine Angew. Math. 717 (2016), 1–33.10.1515/crelle-2014-0031CrossRefGoogle Scholar
Friedlander, J. and Granville, A., Limitations to the equi-distribution of primes. I, Ann. of Math. (2) 129(2) (1989), 363–382.10.2307/1971450CrossRefGoogle Scholar
Fröhlich, A. and Queyrut, J., On the functional equation of the Artin $L$ -function for characters of real representations, Invent. Math. 20 (1973), 125–138.10.1007/BF01404061CrossRefGoogle Scholar
Fröhlich, A., Algebraic number fields: L-functions and Galois properties, in Proceedings of a Symposium Held at the University of Durham, Durham, Sept. 2-12, 1975, A. Fröhlich (ed.), pp. xii+704 (Academic Press [Harcourt Brace Jovanovich, Publishers], London-New York, 1977).Google Scholar
Gallagher, P. X., The large sieve and probabilistic Galois theory, in Analytic number theory (Proceedings of Symposia in Pure Mathematics, vol. XXIV, St. Louis University, St. Louis, MO, 1972), pp. 91–101 (American Mathematical Society, Providence, R.I., 1973).10.1090/pspum/024/0332694CrossRefGoogle Scholar
Gold, R., Hilbert class fields and split extensions, Illinois J. Math. 21(1) (1977), 66–69.10.1215/ijm/1256049501CrossRefGoogle Scholar
Granville, A. and Martin, G., Prime number races, Amer. Math. Monthly 113(1) (2006), 1–33.10.1080/00029890.2006.11920275CrossRefGoogle Scholar
Grenié, L. and Molteni, G., An explicit Chebotarev density theorem under GRH, J. Number Theory 200 (2019), 441–485.10.1016/j.jnt.2018.12.005CrossRefGoogle Scholar
Hasse, H., Number Theory, pp. xvii+638 (Akademie-Verlag, Berlin, 1979). Translated from the third German edition of 1969 by Horst Günter Zimmer.Google Scholar
Hooley, C., On the Pellian equation and the class number of indefinite binary quadratic forms, J. Reine Angew. Math. 353 (1984), 98–131.Google Scholar
Huppert, B., Character theory of finite groups, in De Gruyter Expositions in Mathematics, 25, pp. vi+618 (Walter de Gruyter & Co., Berlin, 1998).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, in American Mathematical Society Colloquium Publications, 53, pp. xii+615 (American Mathematical Society, Providence, RI, 2004). ISBN: 0-8218-3633-1Google Scholar
Kaczorowski, J., On the distribution of primes (mod $4$ ), Analysis 15(2) (1995), 159–171.10.1524/anly.1995.15.2.159CrossRefGoogle Scholar
Kaczorowski, J., On the Shanks-Rényi race problem, Acta Arith. 74(1) (1996), 31–46.10.4064/aa-74-1-31-46CrossRefGoogle Scholar
Kadiri, H., Ng, N. and Wong, P., The least prime ideal in the Chebotarev density theorem, Proc. Amer. Math. Soc. 147(6) (2019), 2289–2303.10.1090/proc/14384CrossRefGoogle Scholar
Katz, N. M., Wieferich past and future, in Topics in finite fields, Contemporary Mathematics, 632, pp. 253–270 (American Mathematical Society, Providence, RI, 2015).10.1090/conm/632/12632CrossRefGoogle Scholar
Klüners, J., Asymptotics of number fields and the Cohen-Lenstra heuristics, J. Théor. Nombres Bordeaux 18(3) (2006), 607–615.10.5802/jtnb.561CrossRefGoogle Scholar
Knapowski, S. and Turán, P., Comparative prime-number theory. I–III, Acta Math. Acad. Sci. Hungar. 13 (1962), 299–364.10.1007/BF02020796CrossRefGoogle Scholar
Komatsu, K., An integral basis of the algebraic number field $\mathbb{Q}\big({a}^{1/\ell },{\zeta}_{\ell}\big)$ , J. Reine Angew. Math. 288 (1976), 152–153.Google Scholar
Kowalski, E., The large sieve and its applications, in Arithmetic geometry, random walks and discrete groups, Cambridge Tracts in Mathematics, 175, pp. xxii+293 (Cambridge University Press, Cambridge, 2008).Google Scholar
Kuperberg, G., Knottedness is in NP, modulo GRH, Adv. Math. 256 (2014), 493–506.10.1016/j.aim.2014.01.007CrossRefGoogle Scholar
Lagarias, J. C., Montgomery, H. L. and Odlyzko, A. M., A bound for the least prime ideal in the Chebotarev density theorem, Invent. Math. 54(3) (1979), 271–296.10.1007/BF01390234CrossRefGoogle Scholar
Lagarias, J. C. and Odlyzko, A. M., Effective versions of the Chebotarev density theorem, in Algebraic number fields: $L$ -functions and Galois properties (Proceedings of a Symposium Held at the University of Durham, 1975), pp. 409–464 (Academic Press, London, 1977).Google Scholar
Lamzouri, Y., Large deviations of the limiting distribution in the Shanks-Rényi prime number race, Math. Proc. Cambridge Philos. Soc. 153(1) (2012), 147–166.10.1017/S030500411200014XCrossRefGoogle Scholar
Lamzouri, Y., Extreme values of class numbers of real quadratic fields, Int. Math. Res. Not. IMRN 2015(22) (2015), 11847–11860.Google Scholar
Larsen, M. and Shalev, A., Characters of symmetric groups: Sharp bounds and applications. Invent. Math. 174(3) (2008), 645–687.10.1007/s00222-008-0145-7CrossRefGoogle Scholar
Lemke Oliver, R. and Soundararajan, K., Unexpected biases in the distribution of consecutive primes, Proc. Natl. Acad. Sci. USA 113(31) (2016). https://doi.org/10.1073/pnas.160536611 CrossRefGoogle ScholarPubMed
Lemmermeyer, F., Reciprocity laws: From Euler to Eisenstein, in Springer Monographs in Mathematics, pp. xx+487 (Springer-Verlag, Berlin, 2000).Google Scholar
Li, X. and Radziwiłł, M., The Riemann zeta function on vertical arithmetic progressions, Int. Math. Res. Not. IMRN 2015(2) (2015), 325–354.10.1093/imrn/rnt197CrossRefGoogle Scholar
Linnik, U. V., On the least prime in an arithmetic progression. I. The basic theorem, Rec. Math. [Mat. Sbornik] N.S. 15(57) (1944), 139–178.Google Scholar
Littlewood, J. E., Sur la distribution des nombres premiers, C. R. Acad. Sci. Paris 158 (1914), 1869–1872.Google Scholar
Littlewood, J. E., On the class-number of the corpus $P\left(\sqrt{-k}\right)$ , Proc. London Math. Soc . (2) 2– 27(1) (1928), 358–372.10.1112/plms/s2-27.1.358CrossRefGoogle Scholar
Malle, G., On the distribution of Galois groups, J. Number Theory 92(2) (2002), 315–329.10.1006/jnth.2001.2713CrossRefGoogle Scholar
Martin, G. and Ng, N., Nonzero values of Dirichlet L-functions in vertical arithmetic progressions, Int. J. Number Theory 9(4) (2013), 813–843.10.1142/S1793042113500140CrossRefGoogle Scholar
Martin, G. and Ng, N., Inclusive prime number races, Trans. Am. Math. Soc. 373(5) (2020) 3561–3607.10.1090/tran/7996CrossRefGoogle Scholar
Martin, G. and Scarfy, J., Comparative prime number theory: A survey, available at https://doi.org/10.48550/arXiv:1202.3408.CrossRefGoogle Scholar
Martin, G., Scarfy, J.,Bahrini, A.,Bajpai, P.,Downey, J., Parvardi, A. H.,Simpson, R. and White, E., A complete annotated bibliography for comparative prime number theory, lecture notes, available at https://personal.math.ubc.ca/~gerg/teaching/592-Fall2018/evolving.pdf.Google Scholar
Martinet, J., Character theory and Artin $L$ -functions, in Algebraic number fields: $L$ -functions and Galois properties (Proceedings of a Symposium Held at the University of Durham, 1975), pp. 1–87 (Academic Press, London, 1977).Google Scholar
Mazur, B., Finding meaning in error terms, Bull. Amer. Math. Soc. 45(2) (2008), 185–228.10.1090/S0273-0979-08-01207-XCrossRefGoogle Scholar
Meng, X., Chebyshev’s bias for products of $k$ primes, Algebra Number Theory 12(2) (2018), 305–341.10.2140/ant.2018.12.305CrossRefGoogle Scholar
Monach, W. R., Numerical investigation of several problems in number theory, Ph.D dissertation, University of Michigan (1980). https://hdl.handle.net/2027.42/158146 Google Scholar
Montgomery, H. L. and Odlyzko, A. M., Large deviations of sums of independent random variables. Acta Arith. 49(4) (1988), 427–434.10.4064/aa-49-4-427-434CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory. I, in Classical theory, Cambridge Studies in Advanced Mathematics, 97, pp. xviii+552 (Cambridge University Press, Cambridge, 2007).Google Scholar
Montgomery, H. L. and Weinberger, J. P., Real quadratic fields with large class number, Math. Ann. 225(2) (1977), 173–176.10.1007/BF01351721CrossRefGoogle Scholar
Mossinghoff, M. J., Oliveira e Silva, T. and Trudgian, T., The distribution of $k$ -free numbers, Math. Comp. 90(328) (2021), 907–929.10.1090/mcom/3581CrossRefGoogle Scholar
Murty, V. K., Explicit formulae and the Lang-Trotter conjecture, number theory (Winnipeg, Man., 1983), Rocky Mountain J. Math. 15(2) (1985), 535–551.10.1216/RMJ-1985-15-2-535CrossRefGoogle Scholar
Murty, V. K., The least prime in a conjugacy class, C. R. Math. Acad. Sci. Soc. R. Can. 22(4) (2000), 129–146.Google Scholar
Murty, M. R., Murty, V. K. and Saradha, N., Modular forms and the Chebotarev density theorem, Amer. J. Math. 110(2) (1988), 253–281.10.2307/2374502CrossRefGoogle Scholar
Murty, M. R. and Murty, V. K., Non-vanishing of $L$ -functions and applications, in Progress in Mathematics, 157, pp. xii+196 (Birkhäuser Verlag, Basel, 1997). ISBN: 3-7643-5801-7Google Scholar
Ng, N., Limiting distributions and zeros of Artin L-functions, Ph.D. thesis, University of British Columbia, 2000. Available at https://www.cs.uleth.ca/~nathanng/RESEARCH/phd.thesis.pdf.Google Scholar
Pierce, L., Turnage-Butterbaugh, C. and Wood, M., An effective Chebotarev density theorem for families of number fields with an application to $\ell$ -torsion in class groups, Invent. Math. 219(2) (2020), 701–778.10.1007/s00222-019-00915-zCrossRefGoogle Scholar
Pizarro-Madariaga, A., Lower bounds for the Artin conductor. Math. Comp. 80(273) (2011), 539–561.10.1090/S0025-5718-2010-02403-2CrossRefGoogle Scholar
Pizarro-Madariaga, A., Irreducible characters with bounded root Artin conductor, Algebra Number Theory 13(9) (2019), 1997–2004.10.2140/ant.2019.13.1997CrossRefGoogle Scholar
Puchta, J. C., On large oscillations of the remainder of the prime number theorems, Acta Math. Hungar. 87(3) (2000), 213–227.10.1023/A:1006711604010CrossRefGoogle Scholar
Roichman, Y., Upper bound on the characters of the symmetric groups, Invent. Math. 125(3) (1996), 451–485.10.1007/s002220050083CrossRefGoogle Scholar
Rubinstein, M. and Sarnak, P., Chebyshev’s bias, Experiment. Math. 3(3) (1994), 173–197.10.1080/10586458.1994.10504289CrossRefGoogle Scholar
Rudnick, Z. and Sarnak, P., Zeros of principal $L$ -functions and random matrix theory, Duke Math. J. 81(2) (1996), 269–322.10.1215/S0012-7094-96-08115-6CrossRefGoogle Scholar
Sagan, B. E., The symmetric group. Representations, combinatorial algorithms, and symmetric functions, in 2nd ed., Graduate Texts in Mathematics, 203, pp. xvi+238 (Springer-Verlag, New York, 2001).Google Scholar
The Sage Developers , SageMath, the Sage Mathematics Software System (Version 8.6), 2019, http://www.sagemath.org.Google Scholar
Sarnak, P., Letter to Barry Mazur on “Chebyshev’s bias” for $\tau (p)$ , https://publications.ias.edu/sites/default/files/MazurLtrMay08.PDF.Google Scholar
Sarnak, P., Class numbers of indefinite binary quadratic forms, II, J. Number Theory 21(3) (1985), 333–346.10.1016/0022-314X(85)90060-5CrossRefGoogle Scholar
Serre, J.-P., Corps locaux, in Deuxième edition, Publications de l’Université de Nancago, VIII, pp. 245 (Hermann, Paris, 1968).Google Scholar
Serre, J.-P., Représentations Linéaires des Groupes Finis, 3rd revised ed. (Hermann, Paris, 1978).Google Scholar
Serre, J.-P., Quelques applications du théorème de densité de Chebotarev, Inst. Hautes Études Sci. Publ. Math. 54 (1981), 323–401.10.1007/BF02698692CrossRefGoogle Scholar
Tenenbaum, G., Introduction à la Théorie Analytique et Probabiliste des Nombres, 4ème édition mise à jour (Belin, Collection Échelles, Paris, 2015).Google Scholar
Thorner, J. and Zaman, A., An explicit bound for the least prime ideal in the Chebotarev density theorem, Algebra Number Theory 11(5) (2017), 1135–1197.10.2140/ant.2017.11.1135CrossRefGoogle Scholar
Thorner, J. and Zaman, A., A unified and improved Chebotarev density theorem, Algebra Number Theory 13(5) (2019), 1039–1068.10.2140/ant.2019.13.1039CrossRefGoogle Scholar
Thorner, J. and Zaman, A., A zero density estimate for Dedekind zeta functions, Int. Math. Res. Not. 2023(8) (2023), 6739–6761.10.1093/imrn/rnac015CrossRefGoogle Scholar
Ulmer, D., Elliptic curves with large rank over function fields, Ann. of Math. (2) 155(1) (2002), 295–315.10.2307/3062158CrossRefGoogle Scholar
Viviani, F., Ramification groups and Artin conductors of radical extensions of $\mathbb{Q}$ , J. Théor. Nombres Bordeaux 16(3) (2004), 779–816.10.5802/jtnb.470CrossRefGoogle Scholar
Weinberger, P. J., Exponents of the class groups of complex quadratic fields, Acta. Arith. 22(2) (1973), 117–124.10.4064/aa-22-2-117-124CrossRefGoogle Scholar
Westlund, J., On the fundamental number of the algebraic number-field $k\left(\sqrt[p]{m}\right)$ , Trans. Amer. Math. Soc. 11(4) (1910), 388–392.Google Scholar
Wilf, H., The asypmtotics of ${e}^{P(z)}$ and the number of elements of each order in ${S}_n$ , Bull. AMS 15 (1986), 228–232.10.1090/S0273-0979-1986-15486-8CrossRefGoogle Scholar
Winckler, B., Théorème de Chebotarev effectif, Preprint, 2013, https://doi.org/10.48550/arXiv:1311.5715.Google Scholar
Wintner, A., On the distribution function of the remainder term of the prime number theorem, Amer. J. Math. 63 (1941), 233–248.10.2307/2371519CrossRefGoogle Scholar
Xi, P., Counting fundamental solutions to the Pell equation with prescribed size, Compos. Math. 154(11) (2018), 2379–2402.10.1112/S0010437X18007480CrossRefGoogle Scholar
Xylouris, T., On the least prime in an arithmetic progression and estimates for the zeros of Dirichlet $L$ -functions, Acta Arith. 150(1) (2011), 65–91.10.4064/aa150-1-4CrossRefGoogle Scholar
Zaman, A., Bounding the least prime ideal in the Chebotarev density theorem, Funct. Approx. Comment. Math. 57(1) (2017), 115–142.10.7169/facm/1651CrossRefGoogle Scholar
Zariski, O. and Samuel, P., Commutative algebra vol. 1, in With the cooperation of I. S. Cohen. Corrected reprinting of the 1958 edition. Graduate Texts in Mathematics, No. 28, pp. xi+329 (Springer-Verlag, New York-Heidelberg-Berlin, 1975).Google Scholar