We give new examples of weak Hilbert spaces.

In a study of the word problem for groups, R. J. Thompson considered a certain group $F$ of self-homeomorphisms of the Cantor set and showed, among other things, that $F$ is finitely presented. Using results of K. S. Brown and R. Geoghegan, M. N. Dyer showed that $F$ is the fundamental group of a finite two-complex ${{Z}^{2}}$ having Euler characteristic one and which is Cockcroft, in the sense that each map of the two-sphere into ${{Z}^{2}}$ is homologically trivial. We show that no proper covering complex of ${{Z}^{2}}$ is Cockcroft. A general result on Cockcroft properties implies that no proper regular covering complex of any finite two-complex with fundamental group $F$ is Cockcroft.

We examine which representations of the absolute Galois group of a field of finite characteristic with image over a finite field of the same characteristic may be constructed by the Galois group’s action on the division points of an appropriate Drinfeld module.

We identify a class of domains of ${{\mathbb{C}}^{n}}$ in which any two commuting holomorphic self-maps have a common fixed point.

Soient 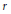$r$ et $p$ deux nombres premiers distincts, soit 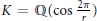$K\,=\,\mathbb{Q}(\cos \,\frac{2\pi }{r})$ , et soit 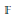$\mathbb{F}$ le corps résiduel de 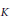$K$ en une place au-dessus de $p$. Lorsque l’image de 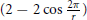$(2\,-\,2\,\cos \,\frac{2\pi }{r})$ dans 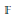$\mathbb{F}$ n’est pas un carré, nous donnons une construction géométrique d’une extension réguliere de 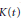$K\left( t \right)$ de groupe de Galois 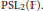$\text{PS}{{\text{L}}_{2}}(\mathbb{F})$ . Cette extension correspond à un revêtement de 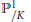${{\mathbb{P}}^{1}}/k$ de « signature 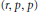$\left( r,\,p,\,p \right)$ » au sens de [3, sec. 6.3], et son existence est prédite par le critère de rigidité de Belyi, Fried, Thompson et Matzat. Sa construction s’obtient en tordant la representation galoisienne associée aux points d’ordre $p$ d’une famille de variétés abéliennes à multiplications réelles par 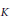$K$ découverte par Tautz, Top et Verberkmoes [6]. Ces variétés abéliennes sont définies sur un corps quadratique, et sont isogènes à leur conjugué galoisien. Notre construction généralise une méthode de Shih [4], [5], que l’on retrouve quand 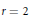$r\,=\,2$ et 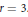$r\,=\,3$.

If $n$ and $m$ are positive integers, necessary and sufficient conditions are given for the existence of a finite commutative ring $R$ with exactly $n$ elements and exactly $m$ prime ideals. Next, assuming the Axiom of Choice, it is proved that if $R$ is a commutative ring and $T$ is a commutative $R$-algebra which is generated by a set $I$, then each chain of prime ideals of $T$ lying over the same prime ideal of $R$ has at most ${{2}^{\left| I \right|}}$ elements. A polynomial ring example shows that the preceding result is best-possible.

We consider ${{C}^{*}}$ -algebras which are inductive limits of finite direct sums of copies of $C([0,\,1])\otimes {{\mathcal{O}}_{2}}$ . For such algebras, the lattice of closed two-sided ideals is proved to be a complete invariant.

We consider maximal operators in the plane, defined by Cantor sets of directions, and show such operators are not bounded on ${{L}^{2}}$ if the Cantor set has positive Hausdorff dimension.

We obtain a homotopy splitting of the forget control map for controlled homeomorphisms over closed manifolds of nonpositive curvature.

Let $\mathbb{T}$ denote the unit circle in the complex plane, and let $X$ be a Banach space that satisfies Burkholder’s $\text{UMD}$ condition. Fix a natural number, $N\,\in \,\mathbb{N}$ . Let $\mathcal{P}$ denote the reverse lexicographical order on ${{\mathbb{Z}}^{N}}$ . For each $f\,\in \,{{L}^{1}}({{\mathbb{T}}^{N}},X)$ , there exists a strongly measurable function $\tilde{f}$ such that formally, for all $\mathbf{n}\,\in \,{{\mathbb{Z}}^{N}},\,\hat{\tilde{f}}\,\left( \mathbf{n} \right)\,=\,-i\,{{sgn }_{\mathcal{P}}}\left( \mathbf{n} \right)\hat{f}\left( \mathbf{n} \right)$ . In this paper, we present a summation method for this conjugate function directly analogous to the martingale methods developed by Asmar and Montgomery-Smith for scalar-valued functions. Using a stochastic integral representation and an application of Garling’s characterization of $\text{UMD}$ spaces, we prove that the associated maximal operator satisfies a weak-type (1, 1) inequality with a constant independent of the dimension $N$.

In this paper, we determine some sufficient conditions for an $A\,+\,XB\left[ X \right]$ domain to be an $\text{HFD}$. As a consequencewe give new examples of $\text{HFDs}$ of the type $A\,+\,XB\left[ X \right]$.

We extend the recent results of R. Latała and O. Guédon about equivalence of ${{L}_{q}}$ -norms of logconcave random variables (Kahane-Khinchin’s inequality) to the quasi-convex case. We construct examples of quasi-convex bodies ${{K}_{n\,}}\subset {{\mathbb{R}}^{n}}$ which demonstrate that this equivalence fails for uniformly distributed vector on ${{K}_{n}}$ (recall that the uniformly distributed vector on a convex body is logconcave). Our examples also show the lack of the exponential decay of the “tail” volume (for convex bodies such decay was proved by M. Gromov and V. Milman).

It is shown that given a local $L$-function defined by Langlands-Shahidi method, there exists a highly ramified character of the group which when is twisted with the original representation leads to a trivial $L$-function.