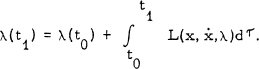Contents
Research Article
Order in Finite Affine Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 407-411
-
- Article
-
- You have access
- Export citation
On Groups with all Composition Factors Isomorphic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 413-415
-
- Article
-
- You have access
- Export citation
On Semigroups of Transformations Acting Transitively on a Set
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-420
-
- Article
-
- You have access
- Export citation
On Some Special Factorizations of (1-xn)/(1-x)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 421-426
-
- Article
-
- You have access
- Export citation
Generating Functions for a Class of Arithmetic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 427-431
-
- Article
-
- You have access
- Export citation
Linear Normed Spaces with Extension Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 433-441
-
- Article
-
- You have access
- Export citation
A Brouwer Type Coincidence Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 443-446
-
- Article
-
- You have access
- Export citation
A New Inversion and Representation Theory for the Laplace Transform
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 447-455
-
- Article
-
- You have access
- Export citation
A Note on Dirichlet Convolutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 457-462
-
- Article
-
- You have access
- Export citation
On Carathéodory's Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-465
-
- Article
-
- You have access
- Export citation
A Property of Entire Functions of Exponential Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 467-472
-
- Article
-
- You have access
- Export citation
On the Functional Equations f(x+iy)| = |f(x)+f(iy)| and |f(x+iy)| = |f(x)-f(iy)| and on Ivory's Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-480
-
- Article
-
- You have access
- Export citation
The Solution of Non-Homogeneous Systems of Differential Equations by Undetermined Coefficients
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-487
-
- Article
-
- You have access
- Export citation
Fatigue Spaces in Electromagnetic-Gravitational Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 489-507
-
- Article
-
- You have access
- Export citation
A Characterization of Deviation from Normality Under Certain Moment Assumptions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 509-514
-
- Article
-
- You have access
- Export citation
Notes and Problems
A Combinatorial Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 515-516
-
- Article
-
- You have access
- Export citation
A Counterexample to a Conjecture of D.F. Sanderson
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 517
-
- Article
-
- You have access
- Export citation
A Global Existence Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 519-520
-
- Article
-
- You have access
- Export citation
R1-Topological Spaces1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 521-523
-
- Article
-
- You have access
- Export citation
On Closed, Totally Bounded Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-526
-
- Article
-
- You have access
- Export citation
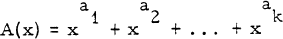 the characteristic polynomial, or briefly, the c-polynomial of A. Any polynomial of such a form we call a c-polynomial and any factorization of a c-polynomial into others of the kind we call a c-factorization. If a c-polynomial cannot be factored in this way we call it c-irreducible. In this note we will determine all c-factorizations of the polynomial 1 + x + x
the characteristic polynomial, or briefly, the c-polynomial of A. Any polynomial of such a form we call a c-polynomial and any factorization of a c-polynomial into others of the kind we call a c-factorization. If a c-polynomial cannot be factored in this way we call it c-irreducible. In this note we will determine all c-factorizations of the polynomial 1 + x + x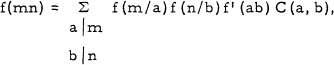
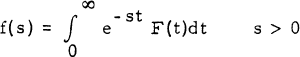
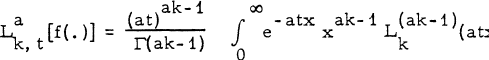
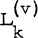 is the Laguerre polynomial of order v, defined by
is the Laguerre polynomial of order v, defined by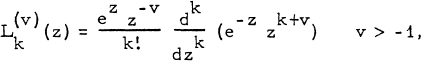
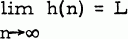 , L finite, then
, L finite, then 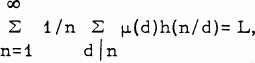 where μ(n) is the Mobius function. This result was extended to functions other than μ(n) in [4]; however, (as first pointed out to the author by Benjamin Volk), the order condition imposed there is unnecessary; in fact, utilizing the result of [3], the following slightly more general theorem has an almost trivial proof.
where μ(n) is the Mobius function. This result was extended to functions other than μ(n) in [4]; however, (as first pointed out to the author by Benjamin Volk), the order condition imposed there is unnecessary; in fact, utilizing the result of [3], the following slightly more general theorem has an almost trivial proof.