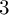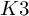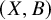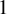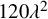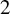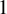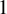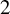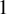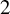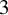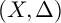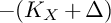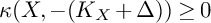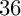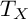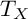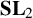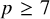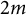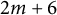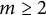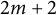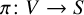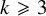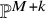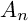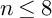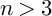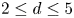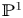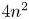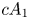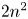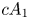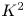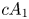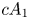199 results in 14Exx
ON THE DEGREE OF IRRATIONALITY OF LOW GENUS
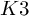 $K3$ SURFACES
$K3$ SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 627-662
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROJECTIVELY FLAT FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 763-812
- Print publication:
- May 2025
-
- Article
- Export citation
TRIANGULATED CHARACTERIZATIONS OF SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-15
-
- Article
- Export citation
Local Normal Forms of Noncommutative Functions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complements and coregularity of Fano varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Covering gonality of symmetric products of curves and Cayley–Bacharach condition on Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant geometry of singular cubic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FANO FOURFOLDS WITH LARGE ANTICANONICAL BASE LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1021-1051
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NON-VANISHING RESULTS CONCERNING THE ANTI-CANONICAL BUNDLE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIGNESS OF THE TANGENT BUNDLE OF A FANO THREEFOLD WITH PICARD NUMBER TWO
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A REMARK ON FUJINO’S WORK ON THE CANONICAL BUNDLE FORMULA VIA PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
On the properness of the moduli space of stable surfaces over
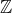 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poncelet’s closure theorem and the embedded topology of conic-line arrangements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 109-123
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Birationally rigid Fano-Mori fibre spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the embedded Nash problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND
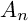 $A_n$ SINGULARITY
$A_n$ SINGULARITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 970-1021
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Low-degree Hurwitz stacks in the Grothendieck ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1784-1849
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
2 n2-inequality for cA1 points and applications to birational rigidity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1551-1595
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

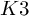
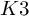
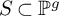
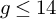
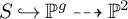 of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most
of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most 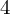
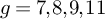
 of degree
of degree