Given a weakly almost additive sequence of continuous functions with bounded variation ${\mathcal {F}}=\{\log f_n\}_{n=1}^{\infty }$ on a subshift X over finitely many symbols, we study properties of a function f on X such that $\lim _{n\to \infty }({1}/{n})\int \log f_n\,d\mu =\int f\,d\mu $ for every invariant measure $\mu $ on X. Under some conditions, we construct a function f on X explicitly, and study a relation between the property of ${\mathcal {F}}$ and some particular types of f. As applications, we study images of Gibbs measures for continuous functions under one-block factor maps. We investigate a relation between the almost additivity of the sequences associated to relative pressure functions and the fiber-wise sub-positive mixing property of a factor map. For a special type of one-block factor maps between shifts of finite type, we study necessary and sufficient conditions for the image of a one-step Markov measure to be a Gibbs measure for a continuous function.

For upper semi-continuous potentials defined on shifts over countable alphabets, this paper ensures sufficient conditions for the existence of a maximizing measure. We resort to the concept of blur shift, introduced by T. Almeida and M. Sobottka as a compactification method for countable alphabet shifts consisting of adding new symbols given by blurred subsets of the alphabet. Our approach extends beyond the Markovian case to encompass more general countable alphabet shifts. In particular, we guarantee a convex characterization and compactness for the set of blur invariant probabilities with respect to the discontinuous shift map.

In this paper, we study the quantitative recurrence 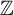properties in the case of $\mathbb {Z}$-extension of Axiom A flows on a Riemannian manifold. We study the asymptotic behavior of the first return time to a small neighborhood of the starting point. We establish results of almost everywhere convergence, and of convergence in distribution with respect to any probability measure absolutely continuous with respect to the infinite invariant measure. In particular, our results apply to geodesic flows on the $\mathbb {Z}$-cover of compact smooth surfaces of negative curvature.

In this article, we prove that the set of well-approximable points $W_\varphi (z) = \{x \in X : d (f^n x, z ) < \varphi (n) \mathrm {\ for\ infinite\ } n \in \mathbb {N}^+\}$ in the shrinking targets problems is distributional chaotic of type 1 for systems with a weak form of the exponential specification property. We apply it to transitive Anosov systems, $\beta $-shifts, etc.

Given any strong orbit equivalence class of minimal Cantor systems and any cardinal number that is finite, countable, or the continuum, we show that there exists a minimal subshift within the class whose number of asymptotic components is exactly the given cardinal. For finite or countable ones, we explicitly construct such examples using $\mathcal {S}$-adic subshifts. We obtain the uncountable case by showing that any topological dynamical system with at most countably many asymptotic components has zero topological entropy. We also construct systems that have arbitrarily high subexponential word complexity, but only one asymptotic component. We deduce that within any strong orbit equivalence class, there exists a minimal subshift whose automorphism group is isomorphic to $\mathbb {Z}$.

Given $\beta>1$, let $T_\beta $ be the $\beta $-transformation on the unit circle $[0,1)$, defined by $T_\beta (x)=\beta x-\lfloor \beta x\rfloor $. For each $t\in [0,1)$, let $K_\beta (t)$ be the survivor set consisting of all $x\in [0,1)$ whose orbit $\{T^n_\beta (x): n\ge 0\}$ never enters the interval $[0,t)$. Kalle et al [Ergod. Th. & Dynam. Sys. 40(9) (2020), 2482–2514] considered the case $\beta \in (1,2]$. They studied the set-valued bifurcation set $\mathscr {E}_\beta :=\{t\in [0,1): K_\beta (t')\ne K_\beta (t)~\text { for all } t'>t\}$ and proved that the Hausdorff dimension function $t\mapsto \dim _H K_\beta (t)$ is a non-increasing Devil’s staircase. In a previous paper [Ergod. Th. & Dynam. Sys. 43(6) (2023), 1785–1828], we determined, for all $\beta \in (1,2]$, the critical value $\tau (\beta ):=\min \{t>0: \eta _\beta (t)=0\}$. The purpose of the present article is to extend these results to all $\beta>1$. In addition to calculating $\tau (\beta )$, we show that: (i) the function $\tau : \beta \mapsto \tau (\beta )$ is left-continuous on $(1,\infty )$ with right-hand limits everywhere, but has countably infinitely many discontinuities; (ii) $\tau $ has no downward jumps; and (iii) there exists an open set $O\subset (1,\infty )$, whose complement $(1,\infty )\setminus O$ has zero Hausdorff dimension, such that $\tau $ is real-analytic, strictly convex, and strictly decreasing on each connected component of O. We also prove several topological properties of the bifurcation set $\mathscr {E}_\beta $. The key to extending the results from $\beta \in (1,2]$ to all $\beta>1$ is an appropriate generalization of the Farey words that are used to parameterize the connected components of the set O. Some of the original proofs from the above-mentioned papers are simplified.

In this paper, we introduce a new technique to study the distribution in residue classes of sets of integers with digit and sum-of-digits restrictions. From our main theorem, we derive a necessary and sufficient condition for integers with missing digits to be uniformly distributed in arithmetic progressions, extending previous results going back to the work of Erdős, Mauduit and Sárközy. Our approach uses Markov chains and does not rely on Fourier analysis as many results of this nature do. Our results apply more generally to the class of multiplicatively invariant sets of integers. This class, defined by Glasscock, Moreira and Richter using symbolic dynamics, is an integer analogue to fractal sets and includes all missing digits sets. We address uniform distribution in this setting, partially answering an open question posed by the same authors.

Recently, Barros et al. [‘On the shortest distance between orbits and the longest common substring problem’, Adv. Math. 344 (2019), 311–339] adopted a dynamical system perspective to study the decay of the shortest distance between orbits. We calculate the Hausdorff dimensions of the exceptional sets arising from the shortest distance between orbits in conformal iterated function systems.

We show that the dynamical system associated by Putnam to a pair of graph embeddings is identical to the shift map on the limit space of a self-similar groupoid action on a graph. Moreover, performing a certain out-split on said graph gives rise to a Katsura–Exel–Pardo groupoid action on the out-split graph whose associated limit space dynamical system is conjugate to the previous one. We characterise the self-similar properties of these groupoids in terms of properties of their defining data, two matrices A, B. We prove a large class of the associated limit spaces are bundles of circles and points that fibre over a totally disconnected space, and the dynamics restricted to each circle are of the form $z\to z^{n}$. Moreover, we find a planar embedding of these spaces, thereby answering a question Putnam posed in his paper.

We study an abstract group of reversible Turing machines. In our model, each machine is interpreted as a homeomorphism over a space which represents a tape filled with symbols and a head carrying a state. These homeomorphisms can only modify the tape at a bounded distance around the head, change the state, and move the head in a bounded way. We study three natural subgroups arising in this model: the group of finite-state automata, which generalizes the topological full groups studied in topological dynamics and the theory of orbit-equivalence; the group of oblivious Turing machines whose movement is independent of tape contents, which generalizes lamplighter groups and has connections to the study of universal reversible logical gates, and the group of elementary Turing machines, which are the machines which are obtained by composing finite-state automata and oblivious Turing machines.

We show that both the group of oblivious Turing machines and that of elementary Turing machines are finitely generated, while the group of finite-state automata and the group of reversible Turing machines are not. We show that the group of elementary Turing machines has undecidable torsion problem. From this, we also obtain that the group of cellular automata (more generally, the automorphism group of any uncountable one-dimensional sofic subshift) contains a finitely generated subgroup with undecidable torsion problem. We also show that the torsion problem is undecidable for the topological full group of a full $\mathbb {Z}^d$-shift on a nontrivial alphabet if and only if $d \geq 2$.

We prove that Brinkmann’s problems are decidable for endomorphisms of $F_n\times F_m$: given $(x,y),(z,w)\in F_n\times F_m$ and $\Phi \in \mathrm {End}(F_n\times F_m)$, it is decidable whether there is some $k\in \mathbb {N}$ such that $(x,y)\Phi ^k=(z,w)$ (or $(x,y)\Phi ^k\sim (z,w)$). We also prove decidability of a two-sided version of Brinkmann’s conjugacy problem for injective endomorphisms which, from the work of Logan, yields a solution to the conjugacy problem in ascending HNN-extensions of $F_n\times F_m$. Finally, we study the dynamics of automorphisms of $F_n\times F_m$ at the infinity, proving that that their dynamics at the infinity is asymptotically periodic, as occurs in the free and free-abelian times free cases.

We define a new class of plane billiards – the “pensive billiard” – in which the billiard ball travels along the boundary for some distance depending on the incidence angle before reflecting, while preserving the billiard rule of equality of the angles of incidence and reflection. This generalizes so-called “puck billiards” proposed by M. Bialy, as well as a “vortex billiard,” that is, the motion of a point vortex dipole in two-dimensional hydrodynamics on domains with boundary. We prove the variational origin and invariance of a symplectic structure for pensive billiards, as well as study their properties including conditions for a twist map, the existence of periodic orbits, etc. We also demonstrate the appearance of both the golden and silver ratios in the corresponding hydrodynamical vortex setting. Finally, we introduce and describe basic properties of pensive outer billiards.

We define a family of discontinuous maps on the circle, called Bowen–Series-like maps, for geometric presentations of surface groups. The family has $2N$ parameters, where $2N$ is the number of generators of the presentation. We prove that all maps in the family have the same topological entropy, which coincides with the volume entropy of the group presentation. This approach allows a simple algorithmic computation of the volume entropy from the presentation only, using the Milnor–Thurston theory for one-dimensional maps.

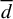For full shifts on finite alphabets, Coelho and Quas [Criteria for $\overline {d}$-continuity. Trans. Amer. Math. Soc. 350(8) (1998), 3257–3268] showed that the map that sends a Hölder continuous potential $\phi $ to its equilibrium state $\mu _\phi $ is $\overline {d}$-continuous. We extend this result to the setting of full shifts on countable (infinite) alphabets. As part of the proof, we show that the map that sends a strongly positive recurrent potential to its normalization is continuous for potentials on mixing countable state Markov shifts.

This paper develops a geometric and analytical framework for studying the existence and stability of pinned pulse solutions in a class of non-autonomous reaction–diffusion equations. The analysis relies on geometric singular perturbation theory, matched asymptotic method and nonlocal eigenvalue problem method. First, we derive the general criteria on the existence and spectral (in)stability of pinned pulses in slowly varying heterogeneous media. Then, as a specific example, we apply our theory to a heterogeneous Gierer–Meinhardt (GM) equation, where the nonlinearity varies slowly in space. We identify the conditions on parameters under which the pulse solutions are spectrally stable or unstable. It is found that when the heterogeneity vanishes, the results for the heterogeneous GM system reduce directly to the known results on the homogeneous GM system. This demonstrates the validity of our approach and highlights how the spatial heterogeneity gives rise to richer pulse dynamics compared to the homogeneous case.

For continuous self-maps of compact metric spaces, we explore the relationship among the shadowable points, sensitive points, and entropy points. Specifically, we show that (1) if the set of shadowable points is dense in the phase space, then any interior point of the set of sensitive points is an entropy point; and (2) if the topological entropy is zero, then the denseness of the set of shadowable points is equivalent to almost chain continuity. In addition, we present a counter-example to a question raised by Ye and Zhang regarding entropy points.

In this paper, we establish variational principles for the metric mean dimension of random dynamical systems with infinite topological entropy. This is based on four types of measure-theoretic ϵ-entropies: Kolmogorov-Sinai ϵ-entropy, Shapira’s ϵ-entropy, Katok’s ϵ-entropy and Brin–Katok local ϵ-entropy. The variational principle, as a fundamental theorem, links topological dynamics and ergodic theory.

We introduce a new conjecture of global asymptotic stability for nonautonomous systems, which is fashioned along the nonuniform exponential dichotomy spectrum and whose restriction to the autonomous case is related to the classical Markus–Yamabe Conjecture: we prove that the conjecture is fulfilled for a family of triangular systems of nonautonomous differential equations satisfying boundedness assumptions. An essential tool to carry out the proof is a necessary and sufficient condition ensuring the property of nonuniform exponential dichotomy for upper block triangular linear differential systems. We also obtain some byproducts having interest on itself, such as the diagonal significance property in terms of the above-mentioned spectrum.

In this work, we introduce the type and typeset invariants for equicontinuous group actions on Cantor sets; that is, for generalized odometers. These invariants are collections of equivalence classes of asymptotic Steinitz numbers associated to the action. We show the type is an invariant of the return equivalence class of the action. We introduce the notion of commensurable typesets and show that two actions which are return equivalent have commensurable typesets. Examples are given to illustrate the properties of the type and typeset invariants. The type and typeset invariants are used to define homeomorphism invariants for solenoidal manifolds.

For a connected Lie group G and an automorphism T of G, we consider the action of T on Sub$_G$, the compact space of closed subgroups of G endowed with the Chabauty topology. We study the action of T on Sub$^p_G$, the closure in Sub$_G$ of the set of closed one-parameter subgroups of G. We relate the distality of the T-action on Sub$^p_G$ with that of the T-action on G and characterise the same in terms of compactness of the closed subgroup generated by T in Aut$(G)$ when T acts distally on the maximal central torus and G is not a vector group. We extend these results to the action of a subgroup of Aut$(G)$ and equate the distal action of any closed subgroup ${\mathcal H}$ on Sub$^p_G$ with that of every element in ${\mathcal H}$. Moreover, we show that a connected Lie group G acts distally on Sub$^p_G$ by conjugation if and only if G is either compact or is isomorphic to a direct product of a compact group and a vector group. Some of our results generalise those of Shah and Yadav.