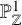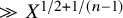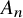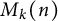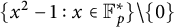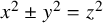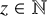Refine listing
Actions for selected content:
283 results in 11Nxx
Oscillation results for the summatory functions of fake
 $\mu $’s
$\mu $’s
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean values of arithmetic functions and application to sums of powers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-13
-
- Article
- Export citation
Smooth numbers in arithmetic progressions to large moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1923-1974
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic curves and spin
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 519-539
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IMPROVED UPPER BOUND ON BRUN’S CONSTANT UNDER GRH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted sieves with switching
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 28 May 2025, pp. 351-372
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POSITIVE DENSITY FOR CONSECUTIVE RUNS OF SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1995-2046
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Chowla conjecture and Landau–Siegel zeroes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 167-187
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SQUARE-FULL VALUES OF QUADRATIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-15
-
- Article
- Export citation
Squarefree values of polynomial discriminants II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure upper bound for a model problem for multiplicative chaos in number theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 29-44
- Print publication:
- July 2025
-
- Article
- Export citation
FONCTIONS ADDITIVES EN BASE DE CANTOR LE LONG DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 06 May 2025, pp. 1807-1865
- Print publication:
- September 2025
-
- Article
- Export citation
NOTE ON A DYNAMICAL GENERALISATION OF THE PRIME NUMBER THEOREM FOR ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-8
-
- Article
- Export citation
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON CHARACTER SUMS OVER SHORT MOVING INTERVALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 13 February 2025, pp. 1395-1427
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean values of multiplicative functions and applications to residue-class distribution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 712-730
-
- Article
- Export citation
Furstenberg systems of pretentious and MRT multiplicative functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 2765-2844
- Print publication:
- September 2025
-
- Article
- Export citation
On Gaussian primes in sparse sets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 181-243
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A function field analog of Jacobi’s theorem on sums of squares and its moments
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 667-683
- Print publication:
- September 2025
-
- Article
- Export citation