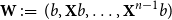Refine listing
Actions for selected content:
181 results in 60Bxx
Free fermionic probability theory and k-theoretic schubert calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-avoiding walk is ballistic on graphs with more than one end
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 October 2025, e179
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditioning Bienaymé–Galton–Watson trees to have large sub-populations
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-42
-
- Article
- Export citation
Contiguity and remote contiguity of some random graphs
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-18
-
- Article
- Export citation
QUANTUM EXPANDERS AND QUANTIFIER REDUCTION FOR TRACIAL VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration on complex Grassmannians, deformed monotone Hurwitz numbers, and interlacing phenomena
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric rigidity of the Wasserstein space over the plane with the maximum metric
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Aldous-Caputo Spectral Gap Conjecture for Hypergraphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 259-298
- Print publication:
- September 2025
-
- Article
- Export citation
Optimal transport on gas networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Fourier coefficients of word maps on unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 681-713
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments of the free Jacobi process: A matrix approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 966-991
- Print publication:
- September 2025
-
- Article
- Export citation
Edge Statistics for Lozenge Tilings of Polygons, II: Airy Line Ensemble
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDED CONJUGACY CLASSES AND CONJUGACY CLASSES SUPPORTING INVARIANT MEASURES AND AUTOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 06 February 2025, pp. 509-514
- Print publication:
- December 2025
-
- Article
- Export citation
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation
Mean field limits of co-evolutionary signed heterogeneous networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central Limit Theorem for tensor products of free variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-33
-
- Article
- Export citation
Gaussian fluctuations for the two-urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 607-641
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STABILITY ANALYSIS FOR STOCHASTIC MCKEAN–VLASOV EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 06 November 2024, e6
-
- Article
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation