Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-21T21:13:17.696Z Has data issue: false hasContentIssue false
  • English
  • Français

Schwarz methods by domain truncation

Published online by Cambridge University Press:  09 June 2022

Martin J. Gander  and
Hui Zhang Open the ORCID record for Hui Zhang [Opens in a new window]
Martin J. Gander
Affiliation:
Department of Mathematics, University of Geneva, CP64, 1211 Geneva 4, Switzerland E-mail: martin.gander@unige.ch
Hui Zhang
Affiliation:
Department of Applied Mathematics and Laboratory for Intelligent Computing & Financial Technology, Xi’an Jiaotong-Liverpool University, Suzhou215123, China E-mail: hui.zhang@xjtlu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Schwarz methods use a decomposition of the computational domain into subdomains and need to impose boundary conditions on the subdomain boundaries. In domain truncation one restricts the unbounded domain to a bounded computational domain and must also put boundary conditions on the computational domain boundaries. In both fields there are vast bodies of literature and research is very active and ongoing. It turns out to be fruitful to think of the domain decomposition in Schwarz methods as a truncation of the domain onto subdomains. Seminal precursors of this fundamental idea are papers by Hagstrom, Tewarson and Jazcilevich (1988), Després (1990) and Lions (1990). The first truly optimal Schwarz method that converges in a finite number of steps was proposed by Nataf (1993), and used precisely transparent boundary conditions as transmission conditions between subdomains. Approximating these transparent boundary conditions for fast convergence of Schwarz methods led to the development of optimized Schwarz methods – a name that has become common for Schwarz methods based on domain truncation. Compared to classical Schwarz methods, which use simple Dirichlet transmission conditions and have been successfully used in a wide range of applications, optimized Schwarz methods are much less well understood, mainly due to their more sophisticated transmission conditions.

A key application of Schwarz methods with such sophisticated transmission conditions turned out to be time-harmonic wave propagation problems, because classical Schwarz methods simply do not work in this case. The past decade has given us many new Schwarz methods based on domain truncation. One review from an algorithmic perspective (Gander and Zhang 2019) showed the equivalence of many of these new methods to optimized Schwarz methods. The analysis of optimized Schwarz methods, however, is lagging behind their algorithmic development. The general abstract Schwarz framework cannot be used for the analysis of these methods, and thus there are many open theoretical questions about their convergence. Just as for practical multigrid methods, Fourier analysis has been instrumental for understanding the convergence of optimized Schwarz methods and for tuning their transmission conditions. Similar to local Fourier mode analysis in multigrid, the unbounded two-subdomain case is used as a model for Fourier analysis of optimized Schwarz methods due to its simplicity. Many aspects of the actual situation, e.g. boundary conditions of the original problem and the number of subdomains, were thus neglected in the unbounded two-subdomain analysis. While this gave important insight, new phenomena beyond the unbounded two-subdomain models were discovered.

This present situation is the motivation for our survey: to give a comprehensive review and precise exploration of convergence behaviours of optimized Schwarz methods based on Fourier analysis, taking into account the original boundary conditions, many-subdomain decompositions and layered media. We consider as our model problem the operator $-\Delta + \eta $ in the diffusive case $\eta>0$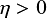 (screened Laplace equation) or the oscillatory case $\eta <0$ 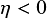(Helmholtz equation), in order to show the fundamental difference in behaviour of Schwarz solvers for these problems. The transmission conditions we study include the lowest-order absorbing conditions (Robin), and also more advanced perfectly matched layers (PMLs), both developed first for domain truncation. Our intensive work over the last two years on this review has led to several new results presented here for the first time: in the bounded two-subdomain analysis for the Helmholtz equation, we see strong influence of the original boundary conditions imposed on the global problem on the convergence factor of the Schwarz methods, and the asymptotic convergence factors with small overlap can differ from the unbounded two-subdomain analysis. In the many-subdomain analysis, we find the scaling with the number of subdomains, e.g. when the subdomain size is fixed, robust convergence of the double-sweep Schwarz method for the free-space wave problem, either with fixed overlap and zeroth-order Taylor conditions or with a logarithmically growing PML, and we find that Schwarz methods with PMLs work like smoothers that converge faster for higher Fourier frequencies; in particular, for the free-space wave problem, plane waves (in the error) passing through interfaces at a right angle converge more slowly. In addition to our main focus on analysis in Sections 2 and 3, we start in Section 1 with an expository historical introduction to Schwarz methods, and in Section 4 we give a brief interpretation of the recently proposed optimal Schwarz methods for decompositions with cross-points from the viewpoint of transmission conditions. We conclude in Section 5 with a summary of open research problems. In Appendix A we provide a Matlab program for a block LU form of an optimal Schwarz method with cross-points, and in Appendix B we give the Maple program for the two-subdomain Fourier analysis.

Type
Research Article
Information
Acta Numerica , Volume 31 , May 2022 , pp. 1 - 134
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Appelo, D., Garcia, F. and Runborg, O. (2020), WaveHoltz: Iterative solution of the Helmholtz equation via the wave equation, SIAM J. Sci. Comput. 42, A1950–A1983.CrossRefGoogle Scholar
Astaneh, A. V. and Guddati, M. N. (2016), A two-level domain decomposition method with accurate interface conditions for the Helmholtz problem, Internat. J. Numer. Methods Engrg 107, 74–90.CrossRefGoogle Scholar
Beams, N. N., Gillman, A. and Hewett, R. J. (2020), A parallel shared-memory implementation of a high-order accurate solution technique for variable coefficient Helmholtz problems, Comput. Math. Appl. 79, 996–1011.CrossRefGoogle Scholar
Bendali, A. and Boubendir, Y. (2006), Non-overlapping domain decomposition method for a nodal finite element method, Numer . Math. 103, 515–537.Google Scholar
Bennequin, D., Gander, M. J. and Halpern, L. (2009), A homographic best approximation problem with application to optimized Schwarz waveform relaxation, Math. Comp. 78, 185–223.CrossRefGoogle Scholar
Bonazzoli, M., Claeys, X., Nataf, F. and Tournier, P.-H. (2021), Analysis of the SORAS domain decomposition preconditioner for non-self-adjoint or indefinite problems, J. Sci. Comput. 89, 19.CrossRefGoogle Scholar
Bonazzoli, M., Dolean, V., Graham, I. G., Spence, E. A. and Tournier, P.-H. (2018), Two-level preconditioners for the Helmholtz equation, in Domain Decomposition Methods in Science and Engineering XXIV (Bjørstad, P. E. et al., eds), Springer, pp. 139–147.CrossRefGoogle Scholar
Bonev, B. and Hesthaven, J. S. (2022), A hierarchical preconditioner for wave problems in quasilinear complexity, SIAM J. Sci Comput. 44, A198–A229.CrossRefGoogle Scholar
Bootland, N., Dolean, V., Jolivet, P. and Tournier, P.-H. (2021a), A comparison of coarse spaces for Helmholtz problems in the high frequency regime, Comput. Math. Appl. 98, 239–253.CrossRefGoogle Scholar
Bootland, N., Dolean, V., Kyriakis, A. and Pestana, J. (2022), Analysis of parallel Schwarz algorithms for time-harmonic problems using block Toeplitz matrices, Electron . Trans. Numer. Anal. 55, 112–141.Google Scholar
Bootland, N., Dwarka, V., Jolivet, P., Dolean, V. and Vuik, C. (2021b), Inexact subdomain solves using deflated GMRES for Helmholtz problems. Available at arXiv:2103.17081.Google Scholar
Boubendir, Y., Antoine, X. and Geuzaine, C. (2012), A quasi-optimal non-overlapping domain decomposition algorithm for the Helmholtz equation, J. Comput. Phys. 231, 262–280.CrossRefGoogle Scholar
Bramble, J. H., Pasciak, J. E., Wang, J. P. and Xu, J. (1991), Convergence estimates for product iterative methods with applications to domain decomposition, Math. Comp. 57, 1–21.CrossRefGoogle Scholar
Cai, X.-C. and Sarkis, M. (1999), A restricted additive Schwarz preconditioner for general sparse linear systems, SIAM J. Sci. Comput. 21, 792–797.CrossRefGoogle Scholar
Chaouqui, F., Gander, M. J. and Santugini-Repiquet, K. (2017), On nilpotent subdomain iterations, in Domain Decomposition Methods in Science and Engineering XXIII (Lee, C.-O. et al., eds), Springer, pp. 125–133.CrossRefGoogle Scholar
Chen, X., Gander, M. J. and Xu, Y. (2021), Optimized Schwarz methods with elliptical domain decompositions, J. Sci. Comput. 86, 1–28.CrossRefGoogle Scholar
Chen, Z. and Xiang, X. (2013a), A source transfer domain decomposition method for Helmholtz equations in unbounded domain, SIAM J. Numer. Anal. 51, 2331–2356.CrossRefGoogle Scholar
Chen, Z. and Xiang, X. (2013b), A source transfer domain decomposition method for Helmholtz equations in unbounded domain, part II: Extensions, Numer . Math. Theory Methods Appl. 6, 538–555.Google Scholar
Chen, Z., Gander, M. J. and Zhang, H. (2016), On the relation between optimized Schwarz methods and source transfer, in Domain Decomposition Methods in Science and Engineering XXII (Dickopf, T. et al., eds), Springer, pp. 217–225.CrossRefGoogle Scholar
Chevalier, P. and Nataf, F. (1998), Symmetrized method with optimized second-order conditions for the Helmholtz equation, in Domain Decomposition Methods 10 (Mandel, J. et al., eds), AMS, pp. 400–407.CrossRefGoogle Scholar
Chniti, C., Nataf, F. and Nier, F. (2006), Improved interface conditions for a non-overlapping domain decomposition of a non-convex polygonal domain, C. R. Math. Acad. Sci. Paris 342, 883–886.CrossRefGoogle Scholar
Chniti, C., Nataf, F. and Nier, F. (2009), Improved interface conditions for 2D domain decomposition with corners: Numerical applications, J. Sci. Comput. 38, 207–228.CrossRefGoogle Scholar
Ciaramella, G. and Gander, M. J. (2018), Analysis of the parallel Schwarz method for growing chains of fixed-sized subdomains: Part III, Electron. Trans. Numer. Anal. 49, 210–243.Google Scholar
Claeys, X. (2019), A new variant of the optimised Schwarz method for arbitrary non-overlapping subdomain partitions. Available at arXiv:1910.05055.Google Scholar
Claeys, X. (2021), Non-local variant of the optimised Schwarz method for arbitrary non-overlapping subdomain partitions, ESAIM Math. Model. Numer. Anal. 55, 429–448.CrossRefGoogle Scholar
Claeys, X. and Parolin, E. (2021), Robust treatment of cross-points in optimized Schwarz methods. Available at arXiv:2003.06657.Google Scholar
Claeys, X., Collino, F., Joly, P. and Parolin, E. (2020), A discrete domain decomposition method for acoustics with uniform exponential rate of convergence using non-local impedance operators, in Domain Decomposition Methods in Science and Engineering XXV (Haynes, R. et al., eds), Springer, pp. 310–317.CrossRefGoogle Scholar
Collino, F., Ghanemi, S. and Joly, P. (2000), Domain decomposition method for harmonic wave propagation: A general presentation, Comput . Methods Appl. Mech. Engrg 184, 171–211.CrossRefGoogle Scholar
Collino, F., Joly, P. and Lecouvez, M. (2020), Exponentially convergent non overlapping domain decomposition methods for the Helmholtz equation, ESAIM Math. Model. Numer. Anal. 54, 775–810.CrossRefGoogle Scholar
Conen, L., Dolean, V., Krause, R. and Nataf, F. (2014), A coarse space for heterogeneous Helmholtz problems based on the Dirichlet-to-Neumann operator, J. Comput. Appl. Math. 271, 83–99.CrossRefGoogle Scholar
Dai, R. (2021), Fast Helmholtz solvers on multi-threaded architectures. PhD thesis, Université de Liège.Google Scholar
Dai, R., Modave, A., Remacle, J.-F. and Geuzaine, C. (2022), Multidirectional sweeping preconditioners with non-overlapping checkerboard domain decomposition for Helmholtz problems, J. Comput. Phys. 453, 110887.CrossRefGoogle Scholar
Deng, Q. (1997), An analysis for a nonoverlapping domain decomposition iterative procedure, SIAM J. Sci. Comput. 18, 1517–1525.CrossRefGoogle Scholar
Després, B. (1990), Décomposition de domaine et problème de Helmholtz, C. R. Math. Acad. Sci. Paris 311, 313–316.Google Scholar
Després, B. (1991), Méthodes de décomposition de domaine pour les problèmes de propagation d’ondes en régime harmonique. PhD thesis, Université Dauphine, Paris IX.Google Scholar
Després, B., Nicolopoulos, A. and Thierry, B. (2021a), Corners and stable optimized domain decomposition methods for the Helmholtz problem, Numer. Math. 149, 779–818.CrossRefGoogle Scholar
Després, B., Nicolopoulos, A. and Thierry, B. (2021b), On domain decomposition methods with optimized transmission conditions and cross-points. Available at hal-03230250.Google Scholar
Dolean, V., Gander, M. J. and Kyriakis, A. (2022), Optimizing transmission conditions for multiple subdomains in the magnetotelluric approximation of Maxwell’s equations, in Domain Decomposition Methods in Science and Engineering XXVI (Brenner, S. C. et al., eds), Springer.Google Scholar
Dryja, M. and Widlund, O. B. (1987), An additive variant of the Schwarz alternating method for the case of many subregions. Technical report, Department of Computer Science, Courant Institute. Also Ultracomputer Note 131.Google Scholar
Du, Y. and Wu, H. (2020), A pure source transfer domain decomposition method for Helmholtz equations in unbounded domain, J. Sci. Comput. 83, 1–29.Google Scholar
Dwarka, V. and Vuik, C. (2020), Scalable convergence using two-level deflation preconditioning for the Helmholtz equation, SIAM J. Sci. Comput. 42, A901–A928.CrossRefGoogle Scholar
Dwarka, V., Tielen, R., Möller, M. and Vuik, C. (2021), Towards accuracy and scalability: Combining isogeometric analysis with deflation to obtain scalable convergence for the Helmholtz equation, Comput . Methods Appl. Mech. Engrg 377, 113694.CrossRefGoogle Scholar
Efstathiou, E. and Gander, M. J. (2003), Why restricted additive Schwarz converges faster than additive Schwarz, BIT 43, 945–959.CrossRefGoogle Scholar
Engquist, B. and Ying, L. (2011a), Sweeping preconditioner for the Helmholtz equation: Hierarchical matrix representation, Commun . Pure Appl. Anal. LXIV, 0697–0735.Google Scholar
Engquist, B. and Ying, L. (2011b), Sweeping preconditioner for the Helmholtz equation: Moving perfectly matched layers, Multiscale Model . Simul. 9, 686–710.Google Scholar
Engquist, B. and Zhao, H. (1998), Absorbing boundary conditions for domain decomposition, Appl. Numer. Math. 27, 341–365.CrossRefGoogle Scholar
Ernst, O. and Gander, M. J. (2012), Why it is difficult to solve Helmholtz problems with classical iterative methods, in Numerical Analysis of Multiscale Problems (Graham, I. et al., eds), Vol. 83 of Lecture Notes in Computational Science and Engineering, Springer, pp. 325–363.CrossRefGoogle Scholar
Eslaminia, M., Elmeliegy, A. M. and Guddati, M. N. (2022), Full waveform inversion through double-sweeping solver, J. Comput. Phys. 453, 110914.CrossRefGoogle Scholar
Fang, J., Qian, J., Zepeda-Núñez, L. and Zhao, H. (2018), A hybrid approach to solve the high-frequency Helmholtz equation with source singularity in smooth heterogeneous media, J. Comput. Phys. 371, 261–279.CrossRefGoogle Scholar
Gander, M. J. (2006), Optimized Schwarz methods, SIAM J. Numer. Anal. 44, 699–731.CrossRefGoogle Scholar
Gander, M. J. (2008), Schwarz methods over the course of time, Electron . Trans. Numer. Anal. 31, 228–255.Google Scholar
Gander, M. J. and Hajian, S. (2015), Analysis of Schwarz methods for a hybridizable discontinuous Galerkin discretization, SIAM J. Numer. Anal. 53, 573–597.CrossRefGoogle Scholar
Gander, M. J. and Hajian, S. (2018), Analysis of Schwarz methods for a hybridizable discontinuous Galerkin discretization: The many-subdomain case, Math. Comp. 87, 1635–1657.CrossRefGoogle Scholar
Gander, M. J. and Kwok, F. (2011), Optimal interface conditions for an arbitrary decomposition into subdomains, in Domain Decomposition Methods in Science and Engineering XIX (Huang, Y. et al., eds), Springer, pp. 101–108.CrossRefGoogle Scholar
Gander, M. J. and Kwok, F. (2012), Best Robin parameters for optimized Schwarz methods at cross points, SIAM J. Sci. Comput. 34, A1849–A1879.CrossRefGoogle Scholar
Gander, M. J. and Nataf, F. (2000), AILU: A preconditioner based on the analytic factorization of the elliptic operator, Numer . Linear Algebra Appl. 7, 505–526.3.0.CO;2-Z>CrossRefGoogle Scholar
Gander, M. J. and Nataf, F. (2005), An incomplete LU preconditioner for problems in acoustics, J. Comput. Acoustics 13, 455–476.CrossRefGoogle Scholar
Gander, M. J. and Santugini, K. (2016), Cross-points in domain decomposition methods with a finite element discretization, Electron . Trans. Numer. Anal. 45, 219–240.Google Scholar
Gander, M. J. and Wanner, G. (2012), From Euler, Ritz, and Galerkin to modern computing, SIAM Rev. 54, 627–666.CrossRefGoogle Scholar
Gander, M. J. and Wanner, G. (2014), The origins of the alternating Schwarz method, in Domain Decomposition Methods in Science and Engineering XXI (Erhel, J. et al., eds), Springer, pp. 487–495.CrossRefGoogle Scholar
Gander, M. J. and Xu, Y. (2014), Optimized Schwarz methods for circular domain decompositions with overlap, SIAM J. Numer. Anal. 52, 1981–2004.CrossRefGoogle Scholar
Gander, M. J. and Xu, Y. (2016), Optimized Schwarz methods for model problems with continuously variable coefficients, SIAM J. Sci. Comput. 38, A2964–A2986.CrossRefGoogle Scholar
Gander, M. J. and Xu, Y. (2017), Optimized Schwarz methods with nonoverlapping circular domain decomposition, Math. Comp. 86, 637–660.CrossRefGoogle Scholar
Gander, M. J. and Zhang, H. (2016), Optimized Schwarz methods with overlap for the Helmholtz equation, SIAM J. Sci. Comput. 38, A3195–A3219.CrossRefGoogle Scholar
Gander, M. J. and Zhang, H. (2019), A class of iterative solvers for the Helmholtz equation: Factorizations, sweeping preconditioners, source transfer, single layer potentials, polarized traces, and optimized Schwarz methods, SIAM Rev. 61, 3–76.CrossRefGoogle Scholar
Gander, M. J. and Zhang, H. (2020), Analysis of double sweep optimized Schwarz methods: The positive definite case, in Domain Decomposition Methods in Science and Engineering XXV (Haynes, R. et al., eds), Springer, pp. 53–64.CrossRefGoogle Scholar
Gander, M. J., Graham, I. G. and Spence, E. A. (2015), Applying GMRES to the Helmholtz equation with shifted Laplacian preconditioning: What is the largest shift for which wavenumber-independent convergence is guaranteed?, Numer. Math. 131, 567–614.CrossRefGoogle Scholar
Gander, M. J., Halpern, L. and Magoules, F. (2007a), An optimized Schwarz method with two-sided Robin transmission conditions for the Helmholtz equation, Internat. J. Numer. Methods Fluids 55, 163–175.CrossRefGoogle Scholar
Gander, M. J., Halpern, L. and Nataf, F. (1999), Optimal convergence for overlapping and non-overlapping Schwarz waveform relaxation, in 11th International Conference on Domain Decomposition Methods (Lai, C.-H. et al., eds), DDM.org, pp. 27–36.Google Scholar
Gander, M. J., Halpern, L. and Nataf, F. (2001), Optimized Schwarz methods, in 12th International Conference on Domain Decomposition Methods (Chan, T. F. et al., eds), DDM.org, pp. 15–27.Google Scholar
Gander, M. J., Halpern, L., Magoulès, F. and Roux, F.-X. (2007b), Analysis of patch substructuring methods, Internat. J. Appl. Math. Comput. Sci. 17, 395–402.CrossRefGoogle Scholar
Gander, M. J., Magoules, F. and Nataf, F. (2002), Optimized Schwarz methods without overlap for the Helmholtz equation, SIAM J. Sci. Comput. 24, 38–60.CrossRefGoogle Scholar
Gong, S., Gander, M. J., Graham, I. G. and Spence, E. A. (2021a), A variational interpretation of restricted additive Schwarz with impedance transmission condition for the Helmholtz problem. Available at arXiv:2103.11379.Google Scholar
Gong, S., Gander, M. J., Graham, I. G., Lafontaine, D. and Spence, E. A. (2022), Convergence of parallel overlapping domain decomposition methods for the Helmholtz equation. Available at arXiv:2106.05218. Submitted to Numer. Math. Google Scholar
Gong, S., Graham, I. G. and Spence, E. A. (2021b), Convergence of restricted additive Schwarz with impedance transmission conditions for discretised Helmholtz problems. Available at arXiv:2110.14495.Google Scholar
Gong, S., Graham, I. G. and Spence, E. A. (2021c), Domain decomposition preconditioners for high-order discretizations of the heterogeneous Helmholtz equation, IMA J. Numer. Anal. 41, 2139–2185.CrossRefGoogle Scholar
Graham, I. G., Spence, E. A. and Vainikko, E. (2017), Recent results on domain decomposition preconditioning for the high-frequency Helmholtz equation using absorption, in Modern Solvers for Helmholtz Problems (Lahaye, D. et al., eds), Springer, pp. 3–26.Google Scholar
Graham, I. G., Spence, E. A. and Zou, J. (2020), Domain decomposition with local impedance conditions for the Helmholtz equation with absorption, SIAM J. Numer. Anal. 58, 2515–2543.CrossRefGoogle Scholar
Grote, M. J. and Tang, J. H. (2019), On controllability methods for the Helmholtz equation, J. Comput. Appl. Math. 358, 306–326.CrossRefGoogle Scholar
Grote, M. J., Nataf, F., Tang, J. H. and Tournier, P.-H. (2020), Parallel controllability methods for the Helmholtz equation, Comput . Methods Appl. Mech. Engrg 362, 112846.CrossRefGoogle Scholar
Guddati, M. N. and Thirunavukkarasu, S. (2013), Improving the convergence of Schwarz methods for Helmholtz equation, in Domain Decomposition Methods in Science and Engineering XX (Bank, R. et al., eds), Springer, pp. 199–206.CrossRefGoogle Scholar
Hackbusch, W. (1994), Iterative Solution of Large Sparse Systems of Equations, Vol. 95 of Applied Mathematical Sciences, Springer.Google Scholar
Haferssas, R., Jolivet, P. and Nataf, F. (2017), An additive Schwarz method type theory for Lions’s algorithm and a symmetrized optimized restricted additive Schwarz method, SIAM J. Sci. Comput. 39, A1345–A1365.CrossRefGoogle Scholar
Hagstrom, T., Tewarson, R. P. and Jazcilevich, A. (1988), Numerical experiments on a domain decomposition algorithm for nonlinear elliptic boundary value problems, Appl. Math. Lett. 1, 299–302.CrossRefGoogle Scholar
Heikkola, E., Ito, K. and Toivanen, J. (2019), A parallel domain decomposition method for the Helmholtz equation in layered media, SIAM J. Sci. Comput. 41, C505–C521.CrossRefGoogle Scholar
Hocking, L. R. and Greif, C. (2021), Optimal complex relaxation parameters in multigrid for complex-shifted linear systems, SIAM J. Matrix Anal. Appl. 42, 475–502.CrossRefGoogle Scholar
Hohage, T., Lehrenfeld, C. and Preuß, J. (2021), Learned infinite elements, SIAM J. Sci. Comput. 43, A3552–A3579.CrossRefGoogle Scholar
Holst, M. and Vandewalle, S. (1997), Schwarz methods: To symmetrize or not to symmetrize, SIAM J. Numer. Anal. 34, 699–722.CrossRefGoogle Scholar
Jacobs, M. and Luo, S. (2021), Numerical solutions for point-source high frequency Helmholtz equation through efficient time propagators for Schrödinger equation, J. Comput. Phys. 438, 110357.CrossRefGoogle Scholar
Japhet, C. (1998), Optimized Krylov–Ventcell method: Application to convection–diffusion problems, in 9th International Conference on Domain Decomposition Methods, DDM.org, pp. 382–389.Google Scholar
Kim, S. and Zhang, H. (2015), Optimized Schwarz method with complete radiation transmission conditions for the Helmholtz equation in waveguides, SIAM J. Numer. Anal. 53, 1537–1558.CrossRefGoogle Scholar
Kim, S. and Zhang, H. (2016), Optimized double sweep Schwarz method by complete radiation boundary conditions, Comput. Math. Appl. 72, 1573–1589.CrossRefGoogle Scholar
Kim, S. and Zhang, H. (2021), Convergence analysis of the continuous and discrete non-overlapping double sweep domain decomposition method based on PMLs for the Helmholtz equation, J. Sci. Comput. 89, 37.CrossRefGoogle Scholar
Kyriakis, A. (2021), Scalable domain decomposition methods for time-harmonic wave propagation problems. PhD thesis, University of Strathclyde.Google Scholar
Lecouvez, M., Stupfel, B., Joly, P. and Collino, F. (2014), Quasi-local transmission conditions for non-overlapping domain decomposition methods for the Helmholtz equation, Comptes Rendus Physique 15, 403–414.Google Scholar
Leng, W. (2015), A fast propagation method for the Helmholtz equation. Available at arXiv:1507.02467.Google Scholar
Leng, W. and Ju, L. (2015), An overlapping domain decomposition preconditioner for the Helmholtz equation. Available at arXiv:1508.02897.Google Scholar
Leng, W. and Ju, L. (2019), An additive overlapping domain decomposition method for the Helmholtz equation, SIAM J. Sci. Comput. 41, A1252–A1277.CrossRefGoogle Scholar
Leng, W. and Ju, L. (2021), A diagonal sweeping domain decomposition method with source transfer for the Helmholtz equation, Commun . Comput. Phys. 29, 357–398.Google Scholar
Leng, W. and Ju, L. (2022), Trace transfer-based diagonal sweeping domain decomposition method for the Helmholtz equation: Algorithms and convergence analysis, J. Comput. Phys. 455, 110980.CrossRefGoogle Scholar
Lions, P.-L. (1988), On the Schwarz alternating method, I, in First International Symposium on Domain Decomposition Methods for Partial Differential Equations (Glowinski, R. et al., eds), SIAM, pp. 1–42.Google Scholar
Lions, P.-L. (1989), On the Schwarz alternating method, II: Stochastic interpretation and order properties, in Second International Symposium on Domain Decomposition Methods for Partial Differential Equations (Chan, T. F. et al., eds), SIAM, pp. 47–70.Google Scholar
Lions, P.-L. (1990), On the Schwarz alternating method, III: A variant for nonoverlapping subdomains, in Third International Symposium on Domain Decomposition Methods for Partial Differential Equations (Chan, T. F. et al., eds), SIAM, pp. 202–223.Google Scholar
Liu, F. and Ying, L. (2016), Recursive sweeping preconditioner for the three-dimensional Helmholtz equation, SIAM J. Sci. Comput. 38, A814–A832.CrossRefGoogle Scholar
Liu, Y. and Xu, X. (2014), A Robin-type domain decomposition method with red-black partition, SIAM J. Numer. Anal. 52, 2381–2399.CrossRefGoogle Scholar
Liu, Y., Ghysels, P., Claus, L. and Li, X. S. (2021), Sparse approximate multifrontal factorization with butterfly compression for high-frequency wave equations, SIAM J. Sci. Comput. 43, S367–S391.CrossRefGoogle Scholar
Loisel, S. (2013), Condition number estimates for the nonoverlapping optimized Schwarz method and the 2-Lagrange multiplier method for general domains and cross points, SIAM J. Numer. Anal. 51, 3062–3083.CrossRefGoogle Scholar
Loisel, S. and Szyld, D. B. (2010), On the geometric convergence of optimized Schwarz methods with applications to elliptic problems, Numer. Math. 114, 697–728.CrossRefGoogle Scholar
Lorca, J. P. L., Beams, N., Beecroft, D. and Gillman, A. (2021), An iterative solver for the HPS discretization applied to three dimensional Helmholtz problems. Available at arXiv:2112.02211.Google Scholar
Lu, W., Qian, J. and Burridge, R. (2016), Babich’s expansion and the fast Huygens sweeping method for the Helmholtz wave equation at high frequencies, J. Comput. Phys. 313, 478–510.CrossRefGoogle Scholar
Lui, S. H. (2009), A Lions non-overlapping domain decomposition method for domains with an arbitrary interface, IMA J. Numer. Anal. 29, 332–349.CrossRefGoogle Scholar
Miller, K. (1965), Numerical analogs to the Schwarz alternating procedure, Numer. Math. 7, 91–103.CrossRefGoogle Scholar
Modave, A., Royer, A., Antoine, X. and Geuzaine, C. (2020), A non-overlapping domain decomposition method with high-order transmission conditions and cross-point treatment for Helmholtz problems, Comput. Methods Appl. Mech. Engrg 368, 113162.CrossRefGoogle Scholar
Nataf, F. (1993), On the use of open boundary conditions in block Gauss–Seidel methods for convection–diffusion equations. Technical report, CMAP (Ecole Polytechnique).Google Scholar
Nataf, F. and Nier, F. (1997), Convergence rate of some domain decomposition methods for overlapping and nonoverlapping subdomains, Numer. Math. 75, 357–377.CrossRefGoogle Scholar
Nataf, F., Rogier, F. and de Sturler, E. (1994), Optimal interface conditions for domain decomposition methods. Technical report, CMAP (Ecole Polytechnique).Google Scholar
Nicholls, D. P., Pérez-Arancibia, C. and Turc, C. (2020), Sweeping preconditioners for the iterative solution of quasiperiodic Helmholtz transmission problems in layered media, J. Sci. Comput. 82, 1–45.CrossRefGoogle Scholar
Nier, F. (1998), Remarques sur les algorithmes de décomposition de domaines, Séminaire Équations aux Dérivées Partielles (Polytechnique) 9, 1–24.Google Scholar
Parolin, É. (2020), Non-overlapping domain decomposition methods with non-local transmission operators for harmonic wave propagation problems. PhD thesis, Institut Polytechnique de Paris.Google Scholar
Petrides, S. and Demkowicz, L. (2021), An adaptive multigrid solver for DPG methods with applications in linear acoustics and electromagnetics, Comput. Math. Appl. 87, 12–26.CrossRefGoogle Scholar
Poulson, J., Engquist, B., Li, S. and Ying, L. (2013), A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations, SIAM J. Sci. Comput. 35, C194–C212.CrossRefGoogle Scholar
Preuss, J. (2021), Learned infinite elements for helioseismology. PhD thesis, Georg-August-Universität Göttingen.Google Scholar
Preuß, J., Hohage, T. and Lehrenfeld, C. (2020), Sweeping preconditioners for stratified media in the presence of reflections, SN Partial Differential Equations and Applications 1, 17.Google Scholar
Qin, L. and Xu, X. (2006), On a parallel Robin-type nonoverlapping domain decomposition method, SIAM J. Numer. Anal. 44, 2539–2558.CrossRefGoogle Scholar
Qin, L., Shi, Z. and Xu, X. (2008), On the convergence rate of a parallel nonoverlapping domain decomposition method, Sci . China Math. 51, 1461–1478.Google Scholar
Riemann, B. (1851a), Foundations of a general theory of functions of a variable complex magnitude. PhD thesis, Göttingen. Translation available at http://science.larouchepac.com/riemann/page/31.Google Scholar
Riemann, B. (1851b), Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. PhD thesis, Göttingen. Available at http://www.emis.de/classics/Riemann/.Google Scholar
Royer, A., Geuzaine, C., Béchet, E. and Modave, A. (2021), A non-overlapping domain decomposition method with perfectly matched layer transmission conditions for the Helmholtz equation. Available at hal-03416187.Google Scholar
Schädle, A. and Zschiedrich, L. (2007), Additive Schwarz method for scattering problems using the PML method at interfaces, in Domain Decomposition Methods in Science and Engineering XVI (Widlund, O. and Keyes, D. E., eds), Springer, pp. 205–212.CrossRefGoogle Scholar
Schädle, A., Zschiedrich, L., Burger, S., Klose, R. and Schmidt, F. (2007), Domain decomposition method for Maxwell’s equations: Scattering off periodic structures, J. Comput. Phys. 226, 477–493.CrossRefGoogle Scholar
Schwarz, H. A. (1870), Über einen Grenzübergang durch alternierendes Verfahren, Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich 15, 272–286.Google Scholar
St-Cyr, A., Gander, M. J. and Thomas, S. J. (2007), Optimized multiplicative additive, and restricted additive Schwarz preconditioning, SIAM J. Sci. Comput. 29, 2402–2425.CrossRefGoogle Scholar
Stolk, C. C. (2013), A rapidly converging domain decomposition method for the Helmholtz equation, J. Comput. Phys. 241, 240–252.CrossRefGoogle Scholar
Stolk, C. C. (2017), An improved sweeping domain decomposition preconditioner for the Helmholtz equation, Adv. Comput. Math. 43, 45–76.CrossRefGoogle Scholar
Stolk, C. C. (2021), A time-domain preconditioner for the Helmholtz equation, SIAM J. Sci. Comput. 43, A3469–A3502.CrossRefGoogle Scholar
Tang, W. P. (1992), Generalized Schwarz splittings, SIAM J. Sci. Statist. Comput. 13, 573–595.CrossRefGoogle Scholar
Taus, M., Zepeda-Núñez, L., Hewett, R. J. and Demanet, L. (2020), L-sweeps: A scalable, parallel preconditioner for the high-frequency Helmholtz equation, J. Comput. Phys. 420, 109706.CrossRefGoogle Scholar
Toselli, A. (1999), Overlapping methods with perfectly matched layers for the solution of the Helmholtz equation, in 11th International Conference on Domain Decomposition Methods (Lai, C.-H. et al., eds), DDM.org, pp. 551–558.Google Scholar
Toselli, A. and Widlund, O. (2005), Domain Decomposition Methods: Algorithms and Theory, Springer.CrossRefGoogle Scholar
Tsuji, P. and Ying, L. (2012), A sweeping preconditioner for Yee’s finite difference approximation of time-harmonic Maxwell’s equations, Front. Math. China 7, 347–363.CrossRefGoogle Scholar
Tsuji, P., Engquist, B. and Ying, L. (2012), A sweeping preconditioner for time-harmonic Maxwell’s equations with finite elements, J. Comput. Phys. 231, 3770–3783.CrossRefGoogle Scholar
Vion, A. and Geuzaine, C. (2014), Double sweep preconditioner for optimized Schwarz methods applied to the Helmholtz problem, J. Comput. Phys. 266, 171–190.CrossRefGoogle Scholar
Vion, A. and Geuzaine, C. (2018), Improved sweeping preconditioners for domain decomposition algorithms applied to time-harmonic Helmholtz and Maxwell problems, ESAIM Proc. Surveys 61, 93–111.CrossRefGoogle Scholar
Weierstrass, K. (1870), Über das sogenannte Dirichlet’sche Princip (Gelesen in der Königl. Akademie der Wissenschaften am 14. Juli 1870), in Mathematische Werke von Karl Weierstrass, Zweiter Band, Abhandlungen, 4, Berlin, p. 53.Google Scholar
Xiang, X. (2019), Double source transfer domain decomposition method for Helmholtz problems, Commun . Comput. Phys. 26, 434–468.CrossRefGoogle Scholar
Xu, X. and Qin, L. (2010), Spectral analysis of Dirichlet–Neumann operators and optimized Schwarz methods with Robin transmission conditions, SIAM J. Numer. Anal. 47, 4540–4568.CrossRefGoogle Scholar
Yang, Z., Wang, L.-L. and Gao, Y. (2021), A truly exact perfect absorbing layer for time-harmonic acoustic wave scattering problems, SIAM J. Sci. Comput. 43, A1027–A1061.CrossRefGoogle Scholar
Zepeda-Núñez, L. and Demanet, L. (2016), The method of polarized traces for the 2D Helmholtz equation, J. Comput. Phys. 308, 347–388.CrossRefGoogle Scholar
Zepeda-Núñez, L. and Demanet, L. (2018), Nested domain decomposition with polarized traces for the 2D Helmholtz equation, SIAM J. Sci. Comput. 40, B942–B981.CrossRefGoogle Scholar
Zepeda-Núñez, L., Hewett, R. J. and Demanet, L. (2014), Preconditioning the 2D Helmholtz equation with polarized traces, in SEG Technical Program Expanded Abstracts 2014, SEG, pp. 3465–3470.CrossRefGoogle Scholar