Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-21T13:05:27.097Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation algorithms in combinatorial scientific computing

Published online by Cambridge University Press:  14 June 2019

Alex Pothen ,
S. M. Ferdous  and
Fredrik Manne
Alex Pothen
Affiliation:
Department of Computer Science, Purdue University, West Lafayette, IN 47907, USA E-mail: apothen@purdue.edu
S. M. Ferdous
Affiliation:
Department of Computer Science, Purdue University, West Lafayette, IN 47907, USA E-mail: sferdou@purdue.edu
Fredrik Manne
Affiliation:
Department of Informatics, University of Bergen, N-5020 Bergen, Norway E-mail: fredrikm@ii.uib.no
Get access Rights & Permissions [Opens in a new window]

Abstract

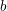We survey recent work on approximation algorithms for computing degree-constrained subgraphs in graphs and their applications in combinatorial scientific computing. The problems we consider include maximization versions of cardinality matching, edge-weighted matching, vertex-weighted matching and edge-weighted $b$-matching, and minimization versions of weighted edge cover and 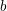$b$-edge cover. Exact algorithms for these problems are impractical for massive graphs with several millions of edges. For each problem we discuss theoretical foundations, the design of several linear or near-linear time approximation algorithms, their implementations on serial and parallel computers, and applications. Our focus is on practical algorithms that yield good performance on modern computer architectures with multiple threads and interconnected processors. We also include information about the software available for these problems.

Type
Research Article
Information
Acta Numerica , Volume 28 , 01 May 2019 , pp. 541 - 633
Copyright
© Cambridge University Press, 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The work of the first two authors was supported in part by US NSF grant CCF-1637534; the US Department of Energy through grant DE-FG02-13ER26135; and the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the DOE Office of Science and the NNSA.

References

REFERENCES 2

Achlioptas, D. and Naor, A. (2005), ‘The two possible values of the chromatic number of a random graph’, Ann. of Math. 162, 1335–1351.Google Scholar
Agrawal, A., Klein, P. N. and Ravi, R. (1993), Cutting down on fill using nested dissection: Provably good elimination orderings. In Graph Theory and Sparse Matrix Computations (George, A., Gilbert, J. R. and Liu, J. W. H., eds), Springer, pp. 31–55.Google Scholar
Al-Herz, A. and Pothen, A. (2019), ‘A $2/3$ -approximation algorithm for vertex-weighted matching’, Discrete Appl. Math., under review. arXiv:1902.05877 Google Scholar
Anstee, R. P. (1987), ‘A polynomial algorithm for $b$ -matchings: An alternative approach’, Inform. Process. Lett. 24, 153–157.Google Scholar
Azad, A. and Buluç, A. (2016), Distributed memory algorithms for maximum cardinality matching on bipartite graphs. In 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS), IEEE, pp. 32–42.Google Scholar
Azad, A., Buluç, A. and Pothen, A. (2017), ‘Computing maximum cardinality matchings in parallel on bipartite graphs via tree grafting’, IEEE Trans. Parallel Distrib. Syst. 28, 44–59.Google Scholar
Azad, A., Buluç, A., Li, X. S., Wang, X. and Langguth, J. (2018), ‘A distributed memory approximation algorithm for maximum weight perfect bipartite matching’, SIAM J. Sci. Comput., under review. arXiv:1801.09809v1 Google Scholar
Azad, A., Langguth, J., Fang, Y., Qi, A. and Pothen, A. (2010), Identifying rare cell populations in comparative flow cytometry. In Algorithms in Bioinformatics: International Workshop on Algorithms in Bioinformatics (WABI), Vol. 6293 of Lecture Notes in Bioinformatics, Springer, pp. 162–175.Google Scholar
Bast, H., Mehlhorn, K., Schäfer, G. and Tamaki, H. (2006), ‘Matching algorithms are fast in sparse random graphs’, Theory Comput. Syst. 39, 3–14.Google Scholar
Bell, C. E. (1994), ‘Weighted matching with vertex weights: An application to scheduling training sessions in NASA space shuttle cockpit simulators’, Europ. J. Oper. Res. 73, 443–449.Google Scholar
Birn, M., Osipov, V., Sanders, P., Schulz, C. and Sitchinava, N. (2013), Efficient parallel and external matching. In Euro-Par 2013 Parallel Processing, Vol. 8097 of Lecture Notes in Computer Science, Springer, pp. 659–670.Google Scholar
Birnbaum, B. and Mathieu, C. (2008), ‘On-line bipartite matching made simple’, ACM SIGACT News 39, 80–87.Google Scholar
Blelloch, G. E., Fineman, J. T. and Shun, J. (2012), Greedy sequential maximal independent set and matching are parallel on average. In Proceedings of the 24th Annual ACM Symposium on Parallelism in Algorithms and Architectures (SPAA ’12), ACM, pp. 308–317.Google Scholar
Blelloch, G. E., Peng, R. and Tangwongsan, K. (2011), Linear work parallel greedy approximate set cover and variants. In Proceedings of the 23rd Annual ACM Symposium on Parallelism in Algorithms and Architectures (SPAA ’11), ACM, pp. 23–32.Google Scholar
Boldi, P. and Vigna, S. (2004), The WebGraph framework I: Compression techniques. In Proceedings of the 13th International Conference on World Wide Web (WWW 2004), ACM, pp. 595–601.Google Scholar
Boldi, P., Marino, A., Santini, M. and Vigna, S. (2014), BUbiNG: Massive crawling for the masses. In Proceedings of the Companion Publication of the 23rd International Conference on World Wide Web, ACM, pp. 227–228.Google Scholar
Buluç, A. and Gilbert, J. R. (2011), ‘The Combinatorial BLAS: Design, implementation and applications’, Internat. J. High Perf. Comput. Appl. 25, 496–509.Google Scholar
Burkard, R., Dell’Amico, M. and Martello, S. (2009), Assignment Problems, SIAM.Google Scholar
Cao, Y. and Sandeep, R. B. (2017), Minimum fill-in: Inapproximability and almost tight lower bounds. In Proceedings of the 28th Annual Symposium on Discrete Algorithms (SODA), SIAM, pp. 875–880.Google Scholar
Choromanski, K. M., Jebara, T. and Tang, K. (2013), Adaptive anonymity via b-matching. In Advances in Neural Information Processing Systems (NIPS 2013) (Burges, C. J. C. et al. , eds), pp. 3192–3200.Google Scholar
Chvatal, V. (1979), ‘A greedy heuristic for the set-covering problem’, Math. Oper. Res. 4, 233–235.Google Scholar
Cohen, J. and Castonguay, P. (2012), Efficient graph matching and coloring on GPUs. Presentation available at: http://on-demand.gputechconf.com/gtc/2012/presentations/S0332-Efficient-Graph-Matching-and-Coloring-on-GPUs.pdf Google Scholar
Coleman, T. F. and Pothen, A. (1987), ‘The null space problem II: Algorithms’, SIAM J. Algebraic Discrete Methods 8, 544–563.Google Scholar
Coleman, T. F., Edenbrandt, A. and Gilbert, J. R. (1986), ‘Predicting fill for sparse orthogonal factorization’, J. Assoc. Comput. Mach. 33, 517–532.Google Scholar
Cormen, T. H., Leiserson, C. E., Rivest, R. L. and Stein, C. (2009), Introduction to Algorithms, MIT Press.Google Scholar
Davis, T. and Hu, Y. (2011), ‘The University of Florida Sparse Matrix Collection’, ACM Trans. Math. Softw. 38, 1:1–1:25.Google Scholar
De Francisci Morales, G., Gionis, A. and Sozio, M. (2011), ‘Social content matching in MapReduce’, Proc. VLDB Endowment 4, 460–469.Google Scholar
Derigs, U. and Metz, A. (1986), ‘On the use of optimal fractional matchings for solving the (integer) matching problem’, Computing 36, 263–270.Google Scholar
Deveci, M., Kaya, K., Uçar, B. and Çatalyürek, Ü. (2013), GPU accelerated maximum cardinality matching algorithms for bipartite graphs. In Proceedings of 19th International Euro-Par Conference on Parallel Processing, pp. 850–861.Google Scholar
Dezső, B., Jüttner, A. and Kovács, P. (2011), ‘LEMON: An open source C++ graph template library’, Electron. Notes Theoret. Comput. Sci. 264, 23–45.Google Scholar
Dobrian, F., Halappanavar, M., Pothen, A. and Al-Herz, A. (2019), ‘A $2/3$ -approximation algorithm for vertex-weighted matching in bipartite graphs’, SIAM J. Sci. Comput. 41, A566–A591.Google Scholar
Drake, D. and Hougardy, S. (2003a), Linear time local improvements for weighted matchings in graphs. In Experimental and Efficient Algorithms, (Jansen, K., Margraf, M., Mastrolilli, M. and Rolim, J., eds), Vol. 2647 of Lecture Notes in Computer Science, Springer, pp. 107–119.Google Scholar
Drake, D. E. and Hougardy, S. (2003b), ‘A simple approximation algorithm for the weighted matching problem’, Inform. Process. Lett. 85, 211–213.Google Scholar
Drake, D. E. and Hougardy, S. (2005), ‘A linear time approximation algorithm for weighted matchings in graphs’, ACM Trans. Algorithms 1, 107–122.Google Scholar
Du, D., Ko, K. and Hu, X. (2012), Design and Analysis of Approximation Algorithms, Springer.Google Scholar
Duan, R. and Pettie, S. (2010), Approximating maximum weight matching in near-linear time. In 2010 IEEE 51st Annual Symposium on Foundations of Computer Science (FOCS ’10), IEEE, pp. 673–682.Google Scholar
Duan, R. and Pettie, S. (2014), ‘Linear-time approximation for maximum weight matching’, J. Assoc. Comput. Mach. 61, 1–23.Google Scholar
Duff, I. S. and Koster, J. (2001), ‘On algorithms for permuting large entries to the diagonal of a sparse matrix’, SIAM J. Matrix Anal. Appl. 22, 973–996.Google Scholar
Duff, I. S. and Uçar, B. (2012), Combinatorial problems in solving linear systems. In Combinatorial Scientific Computing (Naumann, U. and Schenk, O., eds), CRC, pp. 21–68.Google Scholar
Duff, I. S., Kaya, K. and Uçar, B. (2011), ‘Design, implementation, and analysis of maximum transversal algorithms’, ACM Trans. Math. Softw. 38, 13:1–13:31.Google Scholar
Dufossé, F., Kaya, K. and Uçar, B. (2015), ‘Two approximation algorithms for bipartite matching on multicore architectures’, J. Parallel Distrib. Comput. 85, 62–78.Google Scholar
Edmonds, J. (1965), ‘Maximum matching and a polyhedron with 0, 1-vertices’, J. Res. Nat. Bureau Standards 69B, 125–130.Google Scholar
Fagginger Auer, B. O. and Bisseling, R. H. (2012), A GPU algorithm for greedy graph matching. In Facing the Multicore-Challenge II (Keller, R., Kramer, D. and Weiss, J., eds), Springer, pp. 108–119.Google Scholar
Feige, U. and Kilian, J. (1998), ‘Zero knowledge and the chromatic number’, J. Comput. Systems Sci. 57, 187–199.Google Scholar
Ferdous, S., Pothen, A. and Khan, A. (2018), New approximation algorithms for minimum weighted edge cover. In 2018 Proceedings of the Seventh SIAM Workshop on Combinatorial Scientific Computing, SIAM, pp. 97–108.Google Scholar
Fritzson, P. (2014), Principles of Object-Oriented Modeling and Simulation with Modelica 3.3: A Cyber-Physical Approach, Wiley/IEEE.Google Scholar
Gabow, H. N. (1983), An efficient reduction technique for degree-constrained subgraph and bidirected network flow problems. In Proceedings of the 15th Annual ACM Symposium on the Theory of Computing (STOC ’83), ACM, pp. 448–456.Google Scholar
Gabow, H. N. (2018), ‘Data structures for weighted matching and extensions to $b$ -matching and $f$ -factors’, ACM Trans. Algorithms 14, 39:1–39:80.Google Scholar
Gale, D. and Shapley, L. S. (1962), ‘College admissions and the stability of marriage’, Amer. Math. Monthly 69, 9–15.Google Scholar
Gallai, T. (1959), ‘Über extreme Punkt- und Kantenmengen’, Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, Sectio Mathematica 2, 133–138.Google Scholar
Gebremedhin, A. H., Manne, F. and Pothen, A. (2005), ‘What color is your Jacobian? Graph coloring for computing derivatives’, SIAM Review 47, 629–705.Google Scholar
Gebremedhin, A. H., Tarafdar, A., Manne, F. and Pothen, A. (2007), ‘New acyclic and star coloring algorithms with application to computing Hessians’, SIAM J. Sci. Comput. 29, 1042–1072.Google Scholar
George, A. (1973), ‘Nested dissection of a finite element mesh’, SIAM J. Numer. Anal. 10, 345–363.Google Scholar
Georgiadis, G. and Papatriantafilou, M. (2013), ‘Overlays with preferences: Distributed, adaptive approximation algorithms for matching with preference lists’, Algorithms 6, 824–856.Google Scholar
Goemans, M. X. and Williamson, D. P. (1997), The primal–dual method for approximation algorithms and its application to network design problems. In Approximation Algorithms for NP-hard Problems (Hochbaum, D. S., ed.), PWS Publishing Co., pp. 144–191.Google Scholar
Grötschel, M. and Holland, O. (1985), ‘Solving matching problems with linear programming’, Math. Program. 33, 243–259.Google Scholar
Halappanavar, M., Feo, J., Villa, O., Dobrian, F. and Pothen, A. (2012), ‘Approximate weighted matching on emerging manycore and multithreaded architectures’, Internat. J. High Perf. Comput. Appl. 26, 413–430.Google Scholar
Hall, N. G. and Hochbaum, D. S. (1986), ‘A fast approximation algorithm for the multicovering problem’, Discrete Appl. Math. 15, 35–40.Google Scholar
Hanke, S. and Hougardy, S. (2010), New approximation algorithms for the weighted matching problem. Research report 101010, Research Institute for Discrete Mathematics, University of Bonn.Google Scholar
D. S. Hochbaum, ed. (1997), Approximation Algorithms for NP-hard Problems, PWS Publishing Co.Google Scholar
Hogg, J. and Scott, J. (2015), ‘On the use of suboptimal matchings for scaling and ordering sparse symmetric matrices’, Numer. Linear Algebra Appl. 22, 648–663.Google Scholar
Hogg, J. and Scott, J. (2013), ‘Pivoting strategies for tough sparse indefinite systems’, ACM Trans. Math. Softw. 40, 4.Google Scholar
Hopcroft, J. and Karp, R. (1973), ‘An $n^{5/2}$ algorithm for maximum matchings in bipartite graphs’, SIAM J. Comput. 2, 225–231.Google Scholar
Hougardy, S. (2009), Linear time approximation algorithms for degree constrained subgraph problems. In Research Trends in Combinatorial Optimization (Cook, W. J., Lovász, L. and Vygen, J., eds), Springer, pp. 185–200.Google Scholar
Huang, B. C. and Jebara, T. (2011), Fast b-matching via sufficient selection belief propagation. In Proc. 14th International Conference on Artificial Intelligence and Statistics (AISTATS), pp. 361–369.Google Scholar
Huang, D. and Pettie, S. (2017), Approximate generalized matching: $f$ -factors and $f$ -edge covers. arXiv:1706.05761 Google Scholar
Idelberger, A. and Manne, F. (2014), New iterative algorithms for weighted matching. In Norsk Informatikkonferanse 2014. www.nik.no/publikasjoner/ Google Scholar
Jebara, T. and Shchogolev, V. (2006), b-matching for spectral clustering. In Proceedings of the 17th European Conference on Machine Learning (ECML 2006), Vol. 4212 of Lecture Notes in Computer Science, Springer, pp. 679–686.Google Scholar
Jebara, T., Wang, J. and Chang, S.-F. (2009), Graph construction and b-matching for semi-supervised learning. In Proceedings of the 26th Annual International Conference on Machine Learning (ICML ’09), ACM, pp. 441–448.Google Scholar
Juedes, D. and Jones, J. (2012), ‘Coloring Jacobians revisited: A new algorithm for acyclic and star bicoloring’, Optim. Methods Softw. 27, 295–309.Google Scholar
Kang, R. J. and McDiarmid, C. (2015), Colouring random graphs. In Topics in Chromatic Graph Theory (Wilson, R. J. and Beineke, L. W., eds), Cambridge University Press, pp. 199–219.Google Scholar
Karp, R. M. and Sipser, M. (1981), Maximum matching in sparse random graphs. In Proceedings of the 22nd Annual Symposium on Foundations of Computer Science (SFCS 1981), pp. 364–375.Google Scholar
Karp, R. M., Vazirani, U. and Vazirani, V. (1990), An optimal algorithm for on-line bipartite matching. In Proceedings of the 22nd Annual ACM Symposium on Theory of Computing (STOC ’90), ACM, pp. 352–358.Google Scholar
Keiter, E. R., Thornquist, H. K., Hoekstra, R. J., Russo, T. V., Schiek, R. L. and Rankin, E. L. (2011), Parallel transistor-level circuit simulation. In Advanced Simulation and Verification of Electronic and Biological Systems (Li, P., Silveira, L. M. and Feldmann, P., eds), Springer, pp. 1–21.Google Scholar
Khan, A. and Pothen, A. (2016), A new 3/2-approximation algorithm for the b-edge cover problem. In 2016 Proceedings of the Seventh SIAM Workshop on Combinatorial Scientific Computing, SIAM, pp. 52–61.Google Scholar
Khan, A., Choromanski, K., Pothen, A., Ferdous, S., Halappanavar, M. and Tumeo, A. (2018a), Adaptive anonymization of data using b-edge cover. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis (SC ’18), IEEE, pp. 59:1–59:11.Google Scholar
Khan, A. M., Gleich, D. F., Pothen, A. and Halappanavar, M. (2012), A multithreaded algorithm for network alignment via approximate matching. In Proceedings of the International Conference on High Performance Computing, Networking, Storage, and Analysis (SC ’12), IEEE, pp. 64:1–64:11.Google Scholar
Khan, A., Pothen, A. and Ferdous, S. M. (2018b), Parallel algorithms through approximation: b-edge cover. In 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS), IEEE, pp. 22–33.Google Scholar
Khan, A., Pothen, A., Patwary, M. M., Halappanavar, M., Satish, N., Sundaram, N. and Dubey, P. (2016a), Designing scalable b-matching algorithms on distributed memory multiprocessors by approximation. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis (SC ’16), IEEE, pp. 773–783.Google Scholar
Khan, A., Pothen, A., Patwary, M. M., Satish, N., Sundaram, N., Manne, F., Halappanavar, M. and Dubey, P. (2016b), ‘Efficient approximation algorithms for weighted $b$ -matching’, SIAM J. Sci. Comput. 38, S593–S619.Google Scholar
Khuller, S., Vishkin, U. and Young, N. (1994), ‘A primal–dual parallel approximation technique applied to weighted set and vertex covers’, J. Algorithms 17, 280–289.Google Scholar
Knoblauch, V. (2007), Marriage Matching: A conjecture of Donald Knuth. Working papers 2007-15, University of Connecticut, Department of Economics.Google Scholar
Kolmogorov, V. (2009), ‘BLOSSOM V: A new implementation of a minimum cost perfect matching algorithm’, Math. Prog. Comput. 1, 43–67.Google Scholar
Kolyvakis, P., Kalousis, A., Smith, B. and Kiritsis, D. (2018), ‘Biomedical ontology alignment: An approach based on representation learning’, J. Biomed. Semantics 9, 21.Google Scholar
Koufogiannakis, C. and Young, N. E. (2011), ‘Distributed algorithms for covering, packing and maximum weighted matching’, Distrib. Comput. 24, 45–63.Google Scholar
Li, X. S. and Demmel, J. W. (2003), ‘SuperLU_DIST: A scalable distributed-memory sparse direct solver for unsymmetric linear systems’, ACM Trans. Math. Softw. 29, 110–140.Google Scholar
Lovász, L. and Plummer, M. D. (2009), Matching Theory, AMS.Google Scholar
Manlove, D. F. (2013), Algorithmics of Matching Under Preferences, World Scientific.Google Scholar
Manne, F. and Halappanavar, M. (2014), New effective multithreaded matching algorithms. In 2014 IEEE 28th International Parallel and Distributed Processing Symposium (IPDPS), IEEE, pp. 519–528.Google Scholar
Manne, F., Naim, M., Lerring, H. and Halappanavar, M. (2016), On stable marriages and greedy matchings. In 2016 Proceedings of the Seventh SIAM Workshop on Combinatorial Scientific Computing, SIAM, pp. 92–101.Google Scholar
Manshadi, F. M., Awerbuch, B., Gemulla, R., Khandekar, R., Mestre, J. and Sozio, M. (2013), ‘A distributed algorithm for large-scale generalized matching’, Proc. VLDB Endowment 6, 613–624.Google Scholar
Maue, J. and Sanders, P. (2007), Engineering algorithms for approximate weighted matching. In Experimental Algorithms: 6th International Workshop on Experimental and Efficient Algorithms (WEA 2007), Vol. 4525 of Lecture Notes in Computer Science, Springer, pp. 242–255.Google Scholar
McCormick, S. T. (1983), ‘Optimal approximation of sparse Hessians and its equivalence to a graph coloring problem’, Math. Program. 26, 153–171.Google Scholar
McDiarmid, C. (1984), ‘Colouring random graphs’, Ann. Oper. Res. 1, 183–200.Google Scholar
McVitie, D. G. and Wilson, L. B. (1971), ‘The stable marriage problem’, Commun. Assoc. Comput. Mach. 14, 486–490.Google Scholar
Mehlhorn, K. and Näher, S. (1999), LEDA: A platform for combinatorial and geometric computing. www.algorithmic-solutions.com/leda/index.htm Google Scholar
Mehta, A. (2012), ‘Online matching and ad allocation’, Found. Trends. Theor. Comput. Sci. 8, 265–368.Google Scholar
Mendelsohn, N. S. and Dulmage, A. L. (1958), ‘Some generalizations of the problem of distinct representatives’, Canad. J. Math. 10, 230–241.Google Scholar
Mestre, J. (2006), Greedy in approximation algorithms. In Algorithms: 14th Annual European Symposium on Algorithms (ESA 2006), Vol. 4168 of Lecture Notes in Computer Science, Springer, pp. 528–539.Google Scholar
Micali, S. and Vazirani, V. V. (1980), An O (√|V|⋅|E|) algorithm for finding maximum matching in general graphs. In Proceedings of the 21st Annual Symposium on Foundations of Computer Science (SFCS 1980), IEEE, pp. 17–27.Google Scholar
Miller, D. L. and Pekny, J. F. (1995), ‘A staged primal–dual algorithm for perfect $b$ -matching with edge capacities’, ORSA J. Comput. 7, 298–320.Google Scholar
Minoux, M. (1978), Accelerated greedy algorithms for maximizing submodular set functions. In Optimization Techniques: Proceedings of the 8th IFIP Conference on Optimization Techniques (IFIP 1977) (Stoer, J., ed.), Springer, pp. 234–243.Google Scholar
Motwani, R. (1994), ‘Average-case analysis of algorithms for matchings and related problems’, J. Assoc. Comput. Mach. 41, 1329–1356.Google Scholar
Müller-Hannemann, M. and Schwartz, A. (2000), ‘Implementing weighted $b$ -matching algorithms: Insights from a computational study’, J. Exp. Algorithmics 5, 8.Google Scholar
Murphy, R. C., Wheeler, K. B., Barrett, B. W. and Ang, J. A. (2010), Introducing the Graph 500. In Proceedings of the Cray User’s Group Meeting (CUG), 2010.Google Scholar
Naim, M. and Manne, F. (2018), Scalable b-matching on GPUs. In Proceedings of the International Parallel and Distributed Processing Symposium Workshops (IPDPS), pp. 637–646.Google Scholar
Naim, M., Manne, F., Halappanavar, M., Tumeo, A. and Langguth, J. (2015), Optimizing approximate weighted matching on Nvidia Kepler K40. In IEEE 22nd International Conference on High Performance Computing (HiPC 2015), pp. 105–114.Google Scholar
Natanzon, A., Shamir, R. and Sharan, R. (2000), ‘A polynomial approximation for the minimum fill-in problem’, SIAM J. Comput. 30, 1067–1079.Google Scholar
U. Naumann and O. Schenk, eds (2012), Combinatorial Scientific Computing, CRC Press.Google Scholar
Norman, R. Z. and Rabin, M. O. (1959), ‘An algorithm for a minimum cover of a graph’, Proc. Amer. Math. Soc. 10, 315–319.Google Scholar
Olschowka, M. and Neumaier, A. (1996), ‘A new pivoting strategy for Gaussian elimination’, Linear Algebra Appl. 240(suppl. C), 131–151.Google Scholar
Padberg, M. W. and Rao, M. R. (1982), ‘Odd minimum cut-sets and $b$ -matchings’, Math. Oper. Res. 7, 67–80.Google Scholar
Pettie, S. and Sanders, P. (2004), ‘A simpler linear time $2/3-\unicode[STIX]{x1D716}$ approximation for maximum weight matching’, Inform. Process. Lett. 91, 271–276.Google Scholar
Pinar, A., Chow, E. and Pothen, A. (2006), ‘Combinatorial algorithms for computing column space bases that have sparse inverses’, Electron. Trans. Numer. Anal. 22, 122–145.Google Scholar
Pothen, A. (1993), ‘Predicting the structure of sparse orthogonal factors’, Linear Algebra Appl. 194, 183–203.Google Scholar
Pothen, A. and Fan, C.-J. (1990), ‘Computing the block triangular form of a sparse matrix’, ACM Trans. Math. Softw. 16, 303–324.Google Scholar
Preis, R. (1999,), Linear time 1/2-approximation algorithm for maximum weighted matching in general graphs. In 1999 Proceedings of 16th Annual Symposium on Theoretical Aspects of Computer Science (STACS 99), Vol. 1563 of Lecture Notes in Computer Science, Springer, pp. 259–269.Google Scholar
Pulleyblank, W. R. (1973), Faces of matching polyhedra. PhD thesis, Faculty of Mathematics, University of Waterloo.Google Scholar
Rajagopalan, S. and Vazirani, V. V. (1993), Primal–dual RNC approximation algorithms for (multi)-set (multi)-cover and covering integer programs. In Proceedings of 1993 IEEE 34th Annual Foundations of Computer Science (SFCS ’93), IEEE, pp. 322–331.Google Scholar
Schrijver, A. (2003), Combinatorial Optimization: Polyhedra and Efficiency, Vol. A: Paths, Flows, Matchings , Springer.Google Scholar
Sinkhorn, R. and Knopp, P. (1967), ‘Concerning nonnegative matrices and doubly stochastic matrices’, Pacific J. Math. 21, 343–348.Google Scholar
Spencer, T. H. and Mayr, E. W. (1984), Node weighted matching. In Proceedings of the 11th Colloquium on Automata, Languages, and Programming (ICALP), Vol. 172 of Lecture Notes in Computer Science, Springer, pp. 454–464.Google Scholar
Subramanya, A. and Talukdar, P. P. (2014), Graph-Based Semi-Supervised Learning, Vol. 29 of Synthesis Lectures on Artificial Intelligence and Machine Learning, Morgan & Claypool.Google Scholar
Tabatabaee, V., Georgiadis, L. and Tassiulas, L. (2001), ‘QoS provisioning and tracking fluid policies in input queueing switches’, IEEE/ACM Trans. Netw. 9, 605–617.Google Scholar
Tamir, A. and Mitchell, J. S. B. (1998), ‘A maximum $b$ -matching problem arising from median location models with applications to the roommates problem’, Math. Program. 80, 171–194.Google Scholar
Tangwongsan, K. (2011), Efficient parallel approximation algorithms. PhD thesis, Carnegie Mellon University, Pittsburgh, PA.Google Scholar
Vazirani, V. V. (2003), Approximation Algorithms, Springer.Google Scholar
Williamson, D. P. and Shmoys, D. B. (2011), The Design of Approximation Algorithms, Cambridge University Press.Google Scholar
Wilson, L. B. (1972), ‘An analysis of the marriage matching assignment algorithm’, BIT 12, 569–575.Google Scholar
Yannakakis, M. (1981), ‘Computing the minimum fill-in is NP-complete’, SIAM J. Algebraic Discrete Methods 2, 77–79.Google Scholar