Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T06:51:16.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Aggregated Markov processes with negative exponential time interval omission

Published online by Cambridge University Press:  01 July 2016

Frank Ball
Frank Ball*
Affiliation:
University of Nottingham
*
∗Postal address: Department of Mathematics, University of Nottingham, University Park, Nottingham NG7 2RD, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a time reversible, continuous time Markov chain on a finite state space. The state space is partitioned into two sets, termed open and closed, and it is only possible to observe whether the process is in an open or a closed state. Further, short sojourns in either the open or closed states fail to be detected. We consider the situation when the length of minimal detectable sojourns follows a negative exponential distribution with mean μ–1. We show that the probability density function of observed open sojourns takes the form 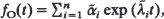, where n is the size of the state space. We present a thorough asymptotic analysis of fO(t) as μ tends to infinity. We discuss the relevance of our results to the modelling of single channel records. We illustrate the theory with a numerical example.

Keywords

TIME REVERSIBLE PROCESSSINGLE CHANNEL GATING KINETICSSPECTRAL DECOMPOSITIONPERTURBATION THEORYIDENTIFIABILITY
Type
Research Article
Information
Advances in Applied Probability , Volume 22 , Issue 4 , December 1990 , pp. 802 - 830
Copyright
Copyright © Applied Probability Trust 1990 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, F. G. and Sansom, M. S. P. (1988a) Single-channel autocorrelation functions: the effects of time interval omission. Biophys. J. 53, 819–832.CrossRefGoogle ScholarPubMed
Ball, F. G. and Sansom, M. S. P. (1988b) Aggregated Markov processes incorporating time interval omission. Adv. Appl. Prob. 20, 546–572.CrossRefGoogle Scholar
Bellman, R. (1960) Introduction to Matrix Analysis. McGraw-Hill, New York.Google Scholar
Colquhoun, D. and Hawkes, A. G. (1977) Relaxation and fluctuations of membrane currents that flow through drug-operated channels. Proc. R. Soc. Lond. B 199, 231–262.Google ScholarPubMed
Colquhoun, D. and Hawkes, A. G. (1981) On the stochastic properties of single ion channels. Proc. Roy. Soc. Lond. B 211, 205–235.Google ScholarPubMed
Colquhoun, D. and Hawkes, A. G. (1987) A note on correlations in single ion channel records. Proc. R. Soc. Lond. B 230, 15–52.Google ScholarPubMed
Colquhoun, D. and Sigworth, F. (1983) Fitting and statistical analysis of single-channel records. In Single-channel Recording , ed. Sakmann, B. and Neher, E., Plenum Press, New York, 135–175.CrossRefGoogle Scholar
Cox, D. R. and Smith, W. L. (1961) Queues. Methuen, London.Google Scholar
Dabrowski, A. R., Mcdonald, D. and Rösler, U. (1989) Renewal properties of ion channels. To appear.CrossRefGoogle Scholar
Forsyth, A. R. (1918) Theory of Functions of a Complex Variable , 3rd edn. Cambridge University Press.Google Scholar
Fredkin, D. R. and Rice, J. A. (1986) On aggregated Markov processes. J. Appl. Prob. 23, 208–214.CrossRefGoogle Scholar
Fredkin, D. R., Montal, M. and Rice, J. A. (1985) Identification of aggregated Markovian models: application to the nicotinic acetylcholine receptor. Proc. Berkeley Conf. in Honor of Jerzy Neyman and Jack Kiefer 1, ed. Le Cam, L. and Ohlsen, R., Wadworth, Belmont, CA, 269–290.Google Scholar
Kelly, F. P. (1979) Reversibility and Stochastic Networks. Wiley, Chichester.Google Scholar
Kerry, C. J., Kits, K. S., Ramsey, R. L., Sansom, M. S. P. and Usherwood, P. N. R. (1987a) Single channel kinetics of a glutamate receptor. Biophys. J. 51, 137–144.CrossRefGoogle ScholarPubMed
Kerry, C. J., Ramsey, R. L., Sansom, M. S. P. and Usherwood, P. N. R. (1987b) Glutamate receptor-channel kinetics: the effect of glutamate concentration. Biophys. J. 53, 39–52.CrossRefGoogle Scholar
Kijima, S. and Kijima, H. (1987a) Statistical analysis of channel current from a membrane patch. I. Some stochastic properties of ion channels or molecular systems in equilibrium. J. Theor. Biol. 128, 423–434.CrossRefGoogle ScholarPubMed
Kijima, S. and Kijima, H. (1987b) Statistical analysis of channel current from a membrane patch. II. A stochastic theory of the multi-channel system in the steady state. J. Theor. Biol. 128, 435–455.CrossRefGoogle Scholar
Roux, B. and Sauve, R. (1985) A general solution to the time interval omission problem applied to single channel analysis. Biophys. J. 48, 149–158.CrossRefGoogle Scholar
Sakmann, B. and Neher, E. (1983) Single-channel Recording. Plenum Press, New York.Google Scholar
Yeo, G. F., Milne, R. K., Edeson, R. O. and Madsen, B. W. (1988) Statistical inference from single channel records: two-state Markov model with limited time resolution. Proc. Roy. Soc. Lond. B 235, 63–94.Google ScholarPubMed
Yeo, G. F., Milne, R. K., Edeson, R. O. and Madsen, B. W. (1989) Superposition properties of independent ion channels. Proc. R. Soc. London B 238, 155–170.Google ScholarPubMed