Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T00:51:30.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Preferential attachment when stable

Part of: Limit theorems Combinatorial probability

Published online by Cambridge University Press:  15 November 2019

Svante Janson ,
Subhabrata Sen  and
Joel Spencer
Svante Janson*
Affiliation:
Uppsala University
Subhabrata Sen*
Affiliation:
Massachusetts Institute of Technology
Joel Spencer*
Affiliation:
New York University
*
*Postal address: Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden. Email address: svante.janson@math.uu.se
**Postal address: Department of Statistics, Harvard University, 1 Oxford Street, SC 712, Cambridge, MA 02138, USA. Email address: subhabratasen@fas.harvard.edu
**Postal address: Department of Statistics, Harvard University, 1 Oxford Street, SC 712, Cambridge, MA 02138, USA. Email address: subhabratasen@fas.harvard.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

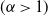We study an urn process with two urns, initialized with a ball each. Balls are added sequentially, the urn being chosen independently with probability proportional to the $\alpha$th power $(\alpha >1)$ of the existing number of balls. We study the (rare) event that the urn compositions are balanced after the addition of 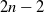$2n-2$ new balls. We derive precise asymptotics of the probability of this event by embedding the process in continuous time. Quite surprisingly, fine control of this probability may be leveraged to derive a lower-tail large deviation principle (LDP) for 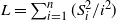$L = \sum_{i=1}^{n} ({S_i^2}/{i^2})$, where 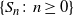$\{S_n \colon n \geq 0\}$ is a simple symmetric random walk started at zero. We provide an alternative proof of the LDP via coupling to Brownian motion, and subsequent derivation of the LDP for a continuous-time analog of L. Finally, we turn our attention back to the urn process conditioned to be balanced, and provide a functional limit law describing the trajectory of the urn process.

Keywords

Urn modellarge deviations

MSC classification

Primary: 60F10: Large deviations 60F17: Functional limit theorems; invariance principles
Secondary: 60C05: Combinatorial probability
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 4 , December 2019 , pp. 1067 - 1108
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. (1978). Stopping times and tightness. Ann. Prob. 6 (2), 335–340.CrossRefGoogle Scholar
Aleksandrov, A. B., Janson, S., Peller, V. V. and Rochberg, R. (2002). An interesting class of operators with unusual Schatten–von Neumann behavior. In Function Spaces, Interpolation Theory and Related Topics (Lund, 2000), pp. 61–149. De Gruyter, Berlin.Google Scholar
Bhattacharya, B. B., Ganguly, S., Lubetzky, E. and Zhao, Y. (2017). Upper tails and independence polynomials in random graphs. Adv. Math. 319, 313–347.CrossRefGoogle Scholar
Bhattacharya, B. B., Ganguly, S., Shao, X. and Zhao, Y. (2019). Upper tails for arithmetic progressions in a random set. To appear in Int. Math. Res. Not. Google Scholar
Billingsley, P. (1968). Convergence of Probability Measures. Wiley, New York.Google Scholar
Billingsley, P. (1974). Conditional distributions and tightness. Ann. Prob. 2, 480–485.CrossRefGoogle Scholar
Chatterjee, S. and Dembo, A. (2016). Nonlinear large deviations. Adv. Math. 299, 396–450.CrossRefGoogle Scholar
Davis, B. (1990). Reinforced random walks. Prob. Theory Relat. Fields 84, 203–229.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (1998). Large Deviation Techniques and Applications, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Eggenberger, F. and Pólya, G. (1923). Über die Statistik verketteter Vorgänge. Z. Angew. Math. Mech. 3 (4), 279–289.CrossRefGoogle Scholar
Eldan, R. (2018). Gaussian-width gradient complexity, reverse log-Sobolev inequalities and non-linear large deviations. Geom. Funct. Anal. 28 (6), 1548–1596.CrossRefGoogle Scholar
Eldan, R. and Gross, R. (2018). Decomposition of mean-field Gibbs distributions into product measures. Electron. J. Probab. 23, paper no. 35, 24.CrossRefGoogle Scholar
Eldan, R. and Gross, R. (2018). Exponential random graphs behave like mixtures of stochastic block models. Ann. Appl. Probab. 28 (6), 3698–3735.CrossRefGoogle Scholar
Hardy, G. H., Littlewood, J. E. and Pólya, G. (1952). Inequalities, 2nd edn. Cambridge University Press, Cambridge.Google Scholar
Janson, S. (1994). Orthogonal Decompositions and Functional Limit Theorems for Random Graph Statistics (Mem. Amer. Math. Soc. 534). American Mathematical Society, Providence, RI.Google Scholar
Janson, S. (1997). Gaussian Hilbert Spaces. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Kallenberg, O. (2002). Foundations of Modern Probability, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Komlós, J., Major, P. and Tusnády, G. (1975). An approximation of partial sums of independent RV’s and the sample DF, I. Z. Wahrscheinlichkeitsth. 32, 111–131.CrossRefGoogle Scholar
Lawler, G. F. and Limic, V. (2010). Random Walk: A Modern Introduction. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Lubetzky, E. and Zhao, Y. (2017). On the variational problem for upper tails in sparse random graphs. Random Structures Algorithms 50 (3), 420–436.CrossRefGoogle Scholar
Mackevičius, V. (1974). On the question of the weak convergence of random processes in the spaces D[0, ∞] (X) (in Russian). Litovsk. Mat. Sb. 14 (4), 117–121, 237. English translation: Lithuanian Math. Trans. (Lithuanian Math. J.) 14 (4), 620–623 (1975).Google Scholar
Oliveira, R. and Spencer, J. (2005). Connectivity transitions in networks with super-linear preferential attachment. Internet Math . 2, 121–163 CrossRefGoogle Scholar
Pólya, G. (1930). Sur quelques points de la théorie des probabilités. Ann. Inst. H. Poincaré Prob. Statist. 1, 117–161.Google Scholar
Whitt, W. (2007). Proofs of the martingale FCLT. Probab. Surv. 4, 268–302.CrossRefGoogle Scholar