Hostname: page-component-6bf8c574d5-zc66z Total loading time: 0 Render date: 2025-03-07T02:32:55.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Thin-ended clusters in percolation in 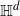$\mathbb{H}^d$

Part of: Equilibrium statistical mechanics Special aspects of infinite or finite groups Special processes

Published online by Cambridge University Press:  10 March 2023

Jan Czajkowski Open the ORCID record for Jan Czajkowski [Opens in a new window]
Jan Czajkowski*
Affiliation:
Wrocław University of Science and Technology
*
*Postal address: Faculty of Pure and Applied Mathematics, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland. Email address: j.czajkowski@pwr.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider Bernoulli bond percolation on a graph nicely embedded in hyperbolic space 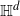$\mathbb{H}^d$ in such a way that it admits a transitive action by isometries of 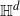$\mathbb{H}^d$ . Let 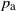$p_{\text{a}}$ be the supremum of all percolation parameters such that no point at infinity of 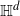$\mathbb{H}^d$ lies in the boundary of the cluster of a fixed vertex with positive probability. Then for any parameter 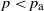$p < p_{\text{a}}$ , almost surely every percolation cluster is thin-ended, i.e. has only one-point boundaries of ends.

Keywords

Bernoulli percolationhyperbolic spacecluster boundaryexponential decay

MSC classification

Primary: 82B43: Percolation
Secondary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory 20F55: Reflection and Coxeter groups
Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 2 , June 2023 , pp. 581 - 610
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babson, E. and Benjamini, I. (1999). Cut sets and normed cohomology with applications to percolation. Proc. Amer. Math. Soc. 127, 589–597.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A. (1999). Metric Spaces of Non-Positive Curvature. Springer, Berlin.CrossRefGoogle Scholar
Burton, R. M.and Keane, M. (1989). Density and uniqueness in percolation. Commun. Math. Phys. 121, 501–505.CrossRefGoogle Scholar
Benjamini, I. and Schramm, O. (1996). Percolation beyond $\textbf Z^d$ , many questions and a few answers. Electron. Commun. Prob. 1, 71–82.CrossRefGoogle Scholar
Benjamini, I. and Schramm, O. (2001). Percolation in the hyperbolic plane. J. Amer. Math. Soc. 14, 487–507.CrossRefGoogle Scholar
Czajkowski, J. (2012). Clusters in middle-phase percolation on hyperbolic plane. In Noncommutative Harmonic Analysis with Applications to Probability III (Banach Center Publications 96), Institute of Mathematics, Polish Academy of Sciences, Warsaw, pp. 99–113.Google Scholar
Czajkowski, J. (2013). Non-uniqueness phase of percolation on reflection groups in $\mathbb{H}^3$ . Preprint. Available at http://arxiv.org/abs/1303.5624.Google Scholar
Diestel, R. (2010). Graph Theory, 4th edn. Springer, New York.CrossRefGoogle Scholar
Grimmett, G. (1999). Percolation. Springer, New York.CrossRefGoogle Scholar
Grimmett, G. and Newman, C. M. (1990). Percolation in $\infty+1$ dimensions. In Disorder in Physical Systems, Oxford University Press, New York, pp. 167–190.Google Scholar
Grimmett, G. and Stirzaker, D. R. (1992). Probability and Random Processes, 2nd edn. Oxford University Press.Google Scholar
Hutchcroft, T. (2019). Percolation on hyperbolic graphs. Geom. Funct. Anal. 29, 766–810.CrossRefGoogle Scholar
Kapovich, I. and Benakli, N. (2002). Boundaries of hyperbolic groups. In Combinatorial and Geometric Group Theory, American Mathematical Society, Providence, RI, pp. 39–93.CrossRefGoogle Scholar
Lalley, S. P. Percolation clusters in hyperbolic tessellations. Geom. Funct. Anal. 11, 971–1030.CrossRefGoogle Scholar
Lalley, S. P. (1998). Percolation on Fuchsian groups. Ann. Inst. H. Poincaré Prob. Statist. 34, 151–177.CrossRefGoogle Scholar
Lyons, R. and Peres, Y. (2013). Probability on Trees and Networks. Cambridge University Press.Google Scholar
Menshikov, M. V. (1986). Coincidence of critical points in percolation problems. Dokl. Akad. Nauk SSSR 288, 1308–1311 (in Russian).Google Scholar
Newman, C. M. and Schulman, L. S. (1981). Infinite clusters in percolation models. J. Statist. Phys. 26, 613–628.CrossRefGoogle Scholar
Pak, I. and Smirnova-Nagnibeda, T. (2000). On non-uniqueness of percolation on nonamenable Cayley graphs. C. R. Acad. Sci. Paris 330, 495–500.CrossRefGoogle Scholar
Sidoravicius, V., Wang, L. and Xiang, K. (2020). Limit set of branching random walks on hyperbolic groups. Preprint. Available at http://arxiv.org/abs/2007.13267v1.Google Scholar
Woess, W. (2000). Random Walks on Infinite Graphs and Groups. Cambridge University Press.CrossRefGoogle Scholar