Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-22T23:25:52.472Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-choice optimal stopping

Part of: Stochastic processes

Published online by Cambridge University Press:  01 July 2016

David Assaf ,
Larry Goldstein  and
Ester Samuel-Cahn
David Assaf
Affiliation:
The Hebrew University of Jerusalem
Larry Goldstein*
Affiliation:
University of Southern California
Ester Samuel-Cahn*
Affiliation:
The Hebrew University of Jerusalem
*
∗∗ Postal address: Department of Mathematics, University of Southern California, 3620 Vermont Avenue, Los Angeles, CA 90089-2532, USA. Email address: larry@math.usc.edu
∗∗∗ Postal address: Department of Statistics, The Hebrew University of Jerusalem, Mount Scopus, Jerusalem 91905, Israel. Email address: scahn@mscc.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Xn,…,X1 be independent, identically distributed (i.i.d.) random variables with distribution function F. A statistician, knowing F, observes the X values sequentially and is given two chances to choose Xs using stopping rules. The statistician's goal is to stop at a value of X as small as possible. Let 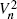equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence 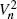for a large class of Fs belonging to the domain of attraction (for the minimum) 𝒟(Gα), where Gα(x) = [1 - exp(-xα)]1(x ≥ 0) (with 1(·) the indicator function). The results are compared with those for the asymptotic behaviour of the classical one-choice value sequence 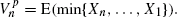, as well as with the ‘prophet value’ sequence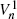

Keywords

Multiple choice stopping ruledomain of attractionprophet value

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 36 , Issue 4 , December 2004 , pp. 1116 - 1147
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗

Supported by the Israel Science Foundation (grant number 879/01).

References

Assaf, D. and Samuel-Cahn, E. (2000). Simple ratio prophet inequalities for a mortal with multiple choices. J. Appl. Prob. 37, 1084–1091.CrossRefGoogle Scholar
Assaf, D., Goldstein, L. and Samuel-Cahn, E. (2002). Ratio prophet inequalities when the mortal has several choices. Ann. Appl. Prob. 12, 972–984.Google Scholar
De Haan, L. (1976). Sample extremes: an elementary introduction. Statist. Neerlandica 30, 161–172.Google Scholar
Kennedy, D. P. and Kertz, R. P. (1990). Limit theorems for threshold-stopped random variables with applications to optimal stopping. Adv. Appl. Prob. 22, 396–411.CrossRefGoogle Scholar
Kennedy, D. P. and Kertz, R. P. (1991). The asymptotic behavior of the reward sequence in the optimal stopping of i.i.d. random variables. Ann. Prob. 19, 329–341.Google Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1983). Extremes and Related Properties of Random Sequences and Processes. Springer, New York.Google Scholar
Resnick, S. I. (1987). Extreme Values, Regular Variation, and Point Processes. Springer, New York.Google Scholar