Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Righter, Rhonda
Shanthikumar, J. George
and
Yamazaki, Genji
1990.
On extremal service disciplines in single-stage queueing systems.
Journal of Applied Probability,
Vol. 27,
Issue. 02,
p.
409.
Righter, Rhonda
Shanthikumar, J. George
and
Yamazaki, Genji
1990.
On extremal service disciplines in single-stage queueing systems.
Journal of Applied Probability,
Vol. 27,
Issue. 2,
p.
409.
Righter, Rhonda
and
Shanthikumar, J. George
1992.
Extremal properties of the FIFO discipline in queueing networks.
Journal of Applied Probability,
Vol. 29,
Issue. 4,
p.
967.
Righter, Rhonda
and
Shanthikumar, J. George
1992.
Extremal properties of the FIFO discipline in queueing networks.
Journal of Applied Probability,
Vol. 29,
Issue. 04,
p.
967.
Liu, Zhen
and
Towsley, Don
1994.
Stochastic Scheduling in in-Forest Networks.
Advances in Applied Probability,
Vol. 26,
Issue. 01,
p.
222.
Liu, Zhen
and
Towsley, Don
1994.
Effects of service disciplines inG/GI/s queueing systems.
Annals of Operations Research,
Vol. 48,
Issue. 4,
p.
401.
Liu, Zhen
and
Towsley, Don
1994.
Stochastic Scheduling in in-Forest Networks.
Advances in Applied Probability,
Vol. 26,
Issue. 1,
p.
222.
Liu, Zhen
Nain, Philippe
and
Towsley, Don
1995.
Sample path methods in the control of queues.
Queueing Systems,
Vol. 21,
Issue. 3-4,
p.
293.
Ohnishi, M.
Maeda, H.
and
Ibaraki, T.
1995.
Optimal scheduling policies in time sharing service systems.
Mathematical and Computer Modelling,
Vol. 22,
Issue. 10-12,
p.
247.
Righter, Rhonda
1996.
Optimal Scheduling of Multiclass Stochastic Systems.
Probability in the Engineering and Informational Sciences,
Vol. 10,
Issue. 2,
p.
229.

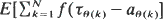 for any non-decreasing and convex function
for any non-decreasing and convex function 