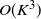1. Introduction
The following corrections need to be applied to [Reference Akbarzadeh and Mahajan1]:
-
1. On p. 11, Equation (19) is missing a term and should be updated as follows:
These formulas are derived by combining Equations (8) and (18). \begin{align*} D^{(h_{d,y})} & = D^{(h_{d})} - \dfrac{(1-\beta) \Phi^{(h_{d})} (c^{(h_d)} - c^{(h_{d, y})}) + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}D^{(h_{d})}}{1 + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}}, \\[5pt] N^{(h_{d,y})} & = N^{(h_{d})} - \dfrac{(1-\beta) \Phi^{(h_{d})} (h_d - h_{d, y}) + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}N^{(h_{d})}}{1 + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}}. \end{align*}
\begin{align*} D^{(h_{d,y})} & = D^{(h_{d})} - \dfrac{(1-\beta) \Phi^{(h_{d})} (c^{(h_d)} - c^{(h_{d, y})}) + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}D^{(h_{d})}}{1 + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}}, \\[5pt] N^{(h_{d,y})} & = N^{(h_{d})} - \dfrac{(1-\beta) \Phi^{(h_{d})} (h_d - h_{d, y}) + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}N^{(h_{d})}}{1 + \beta\rho^{\mathsf{T}}_y \Phi^{(h_{d})}_{\cdot y}}. \end{align*}
-
2. On p. 15, the numbers and indices in Part 4 are incorrect and should be updated as follows:
-
For
 $y = 2$
,
$y = 2$
,
 $h_{2,2} = [0, 0, 0]$
,
$h_{2,2} = [0, 0, 0]$
,
 $N^{(h_{2,2})} = [0, 0, 0]$
, and
$N^{(h_{2,2})} = [0, 0, 0]$
, and
 $D^{(h_{2,2})} = [\!-\!0.21, -0.22, -0.37]$
. Therefore,
$D^{(h_{2,2})} = [\!-\!0.21, -0.22, -0.37]$
. Therefore,
 $\Lambda_{2,2} = \{x \in \mathcal{X} \;:\; N^{(\bar g^{(\mathcal{W}_2)}}(x) \neq N^{(h_{2,2})}(x) \} = \{1, 2, 3\}$
. Now, for each
$\Lambda_{2,2} = \{x \in \mathcal{X} \;:\; N^{(\bar g^{(\mathcal{W}_2)}}(x) \neq N^{(h_{2,2})}(x) \} = \{1, 2, 3\}$
. Now, for each
 $x \in \Lambda_{2,2}$
, we compute
$x \in \Lambda_{2,2}$
, we compute
 $\mu_{2,2}(1) = \mu_{2,2}(2) = \mu_{2,2}(3) = 0.8$
. Therefore,
$\mu_{2,2}(1) = \mu_{2,2}(2) = \mu_{2,2}(3) = 0.8$
. Therefore,
 $\mu^*_{2,2} = 0.8$
.
$\mu^*_{2,2} = 0.8$
.
-
Now
![]() $\mu^*_{2,2} = 0.8$
. Therefore,
$\mu^*_{2,2} = 0.8$
. Therefore,
![]() $\mathcal{W}_3 = \{1, 2, 3\}$
and
$\mathcal{W}_3 = \{1, 2, 3\}$
and
![]() $w(2) = 0.8$
.
$w(2) = 0.8$
.
Some other grammatical errors and typos are highlighted below:
-
1. On p. 6, Figure 1: The lower
 $D^{(h_2)}(x)$
should be changed to
$D^{(h_2)}(x)$
should be changed to
 $D^{(h_1)}(x)$
. The updated figure is as follows:
$D^{(h_1)}(x)$
. The updated figure is as follows:
-
2. On p. 6, Lemma 1: The term ‘piecewise linear’ is repeated and should be removed from the first sentence. The updated lemma should read as follows:
Lemma 1. For any
 $x \in \mathcal{X}$
,
$x \in \mathcal{X}$
,
 $V_\lambda(x)$
is continuous, increasing, and concave in
$V_\lambda(x)$
is continuous, increasing, and concave in
 $\lambda$
. Furthermore, when
$\lambda$
. Furthermore, when
 $\mathcal{X}$
is finite,
$\mathcal{X}$
is finite,
 $V_\lambda(x)$
is piecewise linear in
$V_\lambda(x)$
is piecewise linear in
 $\lambda$
.
$\lambda$
. -
3. On p. 18, proof of Lemma 5: The statement starting with ‘Now (D5) implies that …’ should be changed to ‘The assumption that
 $N^{(g^{(\ell)})}(x)$
is non-increasing in
$N^{(g^{(\ell)})}(x)$
is non-increasing in
 $\ell$
implies that ….’
$\ell$
implies that ….’ -
4. On p. 20, line 4: The second
 $Z^{[g]}$
should be
$Z^{[g]}$
should be
 $\tilde Z^{[g]}$
. So the line after the displayed equation should read as follows: ‘… then
$\tilde Z^{[g]}$
. So the line after the displayed equation should read as follows: ‘… then
 $Z^{[g]} = \left[\begin{array}{c@{\quad}c} 6 & 8 \\[5pt] 14 & 16 \end{array}\right]$
and
$Z^{[g]} = \left[\begin{array}{c@{\quad}c} 6 & 8 \\[5pt] 14 & 16 \end{array}\right]$
and
 $\tilde{Z}^{[g]} = \left[\begin{array}{c@{\quad}c} 5 & 8 \\[5pt] 13 & 15 \end{array}\right]$
.’
$\tilde{Z}^{[g]} = \left[\begin{array}{c@{\quad}c} 5 & 8 \\[5pt] 13 & 15 \end{array}\right]$
.’ -
5. On p. 22, line 3: Where we say ‘relative (percentage) performance improvement’, we should instead say ‘relative (percentage) performance’.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.