Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Weil, Wolfgang
1983.
Convexity and Its Applications.
p.
360.
Weil, Wolfgang
1987.
Stochastic and Integral Geometry.
p.
103.
Well, Wolfgang
1987.
Point processes of cylinders, particles and flats.
Acta Applicandae Mathematicae,
Vol. 9,
Issue. 1-2,
p.
103.
Schneider, Rolf
1988.
Closed convex hypersurfaces with curvature restrictions.
Proceedings of the American Mathematical Society,
Vol. 103,
Issue. 4,
p.
1201.
SCHNEIDER, Rolf
and
WIEACKER, John A.
1993.
Handbook of Convex Geometry.
p.
1349.
Walther, Guenther
1999.
On a generalization of Blaschke's Rolling Theorem and the smoothing of surfaces.
Mathematical Methods in the Applied Sciences,
Vol. 22,
Issue. 4,
p.
301.
Chadœuf, J.
Senoussi, R.
and
Yao, J. F.
2000.
Parametric Estimation of a Boolean Segment Process with Stochastic Restoration Estimation.
Journal of Computational and Graphical Statistics,
Vol. 9,
Issue. 2,
p.
390.
2013.
Stochastic Geometry and its Applications.
p.
453.
Ayala Hoffmann, José
and
Ayala, Victor
2023.
On Disks Enclosed by Smooth Jordan Curves.
Symmetry,
Vol. 15,
Issue. 6,
p.
1140.

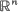 where
where 