Hostname: page-component-cb9f654ff-w5vf4 Total loading time: 0 Render date: 2025-08-09T17:41:52.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Joint temporal and contemporaneous aggregation of random-coefficient AR(1) processes with infinite variance

Part of: Limit theorems Inference from stochastic processes

Published online by Cambridge University Press:  29 April 2020

Vytautė Pilipauskaitė ,
Viktor Skorniakov  and
Donatas Surgailis
Vytautė Pilipauskaitė*
Affiliation:
Aarhus University
Viktor Skorniakov*
Affiliation:
Vilnius University
Donatas Surgailis*
Affiliation:
Vilnius University
*
*Postal address: Aarhus University, Department of Mathematics, Ny Munkegade 118, 8000Aarhus C, Denmark. Email address: vytaute.pilipauskaite@gmail.com
*Postal address: Aarhus University, Department of Mathematics, Ny Munkegade 118, 8000Aarhus C, Denmark. Email address: vytaute.pilipauskaite@gmail.com
*Postal address: Aarhus University, Department of Mathematics, Ny Munkegade 118, 8000Aarhus C, Denmark. Email address: vytaute.pilipauskaite@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss the joint temporal and contemporaneous aggregation of N independent copies of random-coefficient AR(1) processes driven by independent and identically distributed innovations in the domain of normal attraction of an $\alpha$-stable distribution, 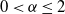$0< \alpha \le 2$, as both N and the time scale n tend to infinity, possibly at different rates. Assuming that the tail distribution function of the random autoregressive coefficient regularly varies at the unit root with exponent 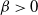$\beta > 0$, we show that, for 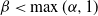$\beta < \max (\alpha, 1)$, the joint aggregate displays a variety of stable and non-stable limit behaviors with stability index depending on $\alpha$, 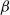$\beta$ and the mutual increase rate of N and n. The paper extends the results of Pilipauskaitė and Surgailis (2014) from 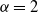$\alpha =2$ to 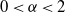$0 < \alpha < 2$.

Keywords

Autoregressive modelpanel datamixture distributioninfinite variancelong-range dependencescaling transitionPoisson random measureasymptotic self-similarity

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 62M10: Time series, auto-correlation, regression, etc.

Information

Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 1 , March 2020 , pp. 237 - 265
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barndorff-Nielsen, O. E. (2001). Superposition of Ornstein–Uhlenbeck type processes. Theory Prob. Appl. 45, 175–194.CrossRefGoogle Scholar
Beran, J., Feng, Y., Gosh, S. andKulik, R. (2013). Long-Memory Processes: Probabilistic Properties and Statistical Methods. Springer, New York.CrossRefGoogle Scholar
Beran, J., Schützner, M. andGhosh, S. (2010). From short to long memory: aggregation and estimation. Comput. Statist. Data Anal. 54, 2432–2442.CrossRefGoogle Scholar
Celov, D., Leipus, R. andPhilippe, A. (2007). Time series aggregation, disaggregation, and long memory. Lith. Math. J. 47, 379–393.CrossRefGoogle Scholar
Celov, D., Leipus, R. andPhilippe, A. (2010). Asymptotic normality of the mixture density estimator in a disaggregation scheme. J. Nonparametric Statist. 22, 425–442.CrossRefGoogle Scholar
Dombry, C. andKaj, I. (2011). The on-off network traffic under intermediate scaling. Queueing Systems 69, 29–44.CrossRefGoogle Scholar
Embrechts, P. andGoldie, C. M. (1980). On closure and factorization properties of subexponential and related distributions. J. Austral. Math. Soc. Ser. A 29, 243–256.CrossRefGoogle Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, vol. II, 2nd edn. Wiley, New York.Google Scholar
Gaigalas, R. (2006). A Poisson bridge between fractional Brownian motion and stable Lévy motion. Stoch. Process. Appl. 116, 447–462.CrossRefGoogle Scholar
Gaigalas, R. andKaj, I. (2003). Convergence of scaled renewal processes and a packet arrival model. Bernoulli 9, 671–703.CrossRefGoogle Scholar
Grahovac, D., Leonenko, N. N. andTaqqu, M. S. (2019). The multifaceted behavior of integrated supOU processes: the infinite variance case. To appear in J. Theoret. Prob. doi:10.1007/s10959-019-00935-8.CrossRefGoogle Scholar
Granger, C. W. J. (1980). Long memory relationship and the aggregation of dynamic models. J. Econometrics 14, 227–238.CrossRefGoogle Scholar
Ibragimov, I. andLinnik, Y. (1971). Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, Groningen.Google Scholar
Jirak, M. (2013). Limit theorems for aggregated linear processes. Adv. Appl. Prob. 45, 520–544.CrossRefGoogle Scholar
Kaj, I. (2005). Limiting fractal random processes in heavy-tailed systems. In Fractals in Engineering: New Trends in Theory and Applications, eds J. Lévy-Véhel and E. Lutton, pp. 199–217. Springer, London.CrossRefGoogle Scholar
Kaj, I. andTaqqu, M. S. (2008). Convergence to fractional Brownian motion and to the Telecom process: the integral representation approach. In In and Out of Equilibrium 2, eds V. Sidoravicius and M. E. Vares, pp. 383–427. Birkhäuser, Basel.CrossRefGoogle Scholar
Leipus, R., Oppenheim, G., Philippe, A. andViano, M.-C. (2006). Orthogonal series density estimation in a disaggregation scheme. J. Statist. Planning Infer. 136, 2547–2571.CrossRefGoogle Scholar
Leipus, R., Philippe, A., Puplinskaitė, D. andSurgailis, D. (2014). Aggregation and long memory: recent developments. J. Indian Statist. Assoc. 52, 71–101.Google Scholar
Leipus, R., Philippe, A., Pilipauskaitė, V. andSurgailis, D. (2017). Nonparametric estimation of the distribution of the autoregressive coefficient from panel random-coefficient AR(1) data. J. Multivariate Anal. 153, 121–135.CrossRefGoogle Scholar
Leipus, R., Philippe, A., Pilipauskaitė, V. andSurgailis, D. (2019+). Estimating long memory in panel random-coefficient AR(1) data. To appear in J. Time Ser. Anal. Available at arXiv:1710.09735v3 [math.ST].CrossRefGoogle Scholar
Leipus, R., Philippe, A., Pilipauskaitė, V. andSurgailis, D. (2019). Sample autocovariances of random-coefficient AR(1) panel model. Electron. J. Statist. 13, 4527–4572.CrossRefGoogle Scholar
Levy, J. B. andTaqqu, M. S. (2000). Renewal reward processes with heavy-tailed interrenewal times and heavy-tailed rewards. Bernoulli 6, 23–44.CrossRefGoogle Scholar
Mikosch, T. (2003). Modelling dependence and tails of financial time series. In Extreme Values in Finance, Telecommunications and the Environment, eds B. Finkenstädt and H. Rootzén, pp. 185–286. Chapman & Hall, New York.Google Scholar
Mikosch, T., Resnick, S., Rootzén, H. andStegeman, A. (2002). Is network traffic approximated by stable Lévy motion or fractional Brownian motion? Ann. Appl. Prob. 12, 23–68.CrossRefGoogle Scholar
Oppenheim, G. andViano, M.-C. (2004). Aggregation of random parameters Ornstein–Uhlenbeck or AR processes: some convergence results. J. Time Ser. Anal. 25, 335–350.CrossRefGoogle Scholar
Pilipauskaitė, V. (2017). Limit theorems for spatio-temporal models with long-range dependence. Doctoral dissertation, Vilnius University.Google Scholar
Pilipauskaitė, V. andSurgailis, D. (2014). Joint temporal and contemporaneous aggregation of random-coefficient AR(1) processes. Stoch. Process. Appl. 124, 1011–1035.CrossRefGoogle Scholar
Pilipauskaitė, V. andSurgailis, D. (2016). Anisotropic scaling of random grain model with application to network traffic. J. Appl. Prob. 53, 857–879.CrossRefGoogle Scholar
Pipiras, V., Taqqu, M. S. andLevy, L. B. (2004). Slow, fast and arbitrary growth conditions for renewal reward processes when the renewals and the rewards are heavy-tailed. Bernoulli 10, 121–163.CrossRefGoogle Scholar
Puplinskaitė, D. andSurgailis, D. (2009). Aggregation of random coefficient AR1(1) process with infinite variance and common innovations. Lith. Math. J. 49, 446–463.CrossRefGoogle Scholar
Puplinskaitė, D. andSurgailis, D. (2010). Aggregation of random coefficient AR1(1) process with infinite variance and idiosyncratic innovations. Adv. Appl. Prob. 42, 509–527.CrossRefGoogle Scholar
Rajput, B. S. andRosinski, J. (1989). Spectral representations of infinitely divisible processes. Prob. Theory Relat. Fields 82, 451–487.CrossRefGoogle Scholar
Robinson, P. M. (1978). Statistical inference for a random coefficient autoregressive model. Scand. J. Statist. 5, 163–168.Google Scholar
Samorodnitsky, G. andTaqqu, M. S. (1994). Stable Non-Gaussian Random Processes. Chapman & Hall, New York.Google Scholar
Taqqu, M. S., Willinger, W. andSherman, R. (1997). Proof of a fundamental result in self-similar traffic modeling. Comput. Commun. Rev. 27, 5–23.CrossRefGoogle Scholar
Zaffaroni, P. (2004). Contemporaneous aggregation of linear dynamic models in large economies. J. Econometrics 120, 75–102.CrossRefGoogle Scholar
Zolotarev, V. M. (1986). One-Dimensional Stable Distributions. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar