Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kersting, Götz
Pardo, Juan Carlos
and
Siri-Jégousse, Arno
2014.
Total internal and external lengths of the Bolthausen-Sznitman coalescent.
Journal of Applied Probability,
Vol. 51,
Issue. A,
p.
73.
Birkner, Matthias
Dahmer, Iulia
Diehl, Christina S.
and
Kersting, Götz
2024.
The joint fluctuations of the lengths of the Beta(2−α,α)-coalescents.
The Annals of Applied Probability,
Vol. 34,
Issue. 1A,

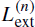 of an initial sample of
of an initial sample of 