Article contents
Study of performance of an internal strut-based thrust vectoring control system
Published online by Cambridge University Press: 12 December 2024
Abstract
In this paper the performance of an internal strut-based thrust vector control (TVC) system has been studied at different expansion conditions of propulsion nozzle. The TVC system uses a cylindrical strut inserted through the diverging wall of a supersonic nozzle. This TVC system can be construed as an alternative to secondary injection TVC method. The nozzle had an expansion ratio of 1.545 and nozzle pressure ratio (NPR) of 6.61 for optimum expansion. Numerical simulations were performed at over-expansion (NPR = 3.94) and under-expansion (NPR = 7.89) conditions for four strut locations (xs) and five strut heights (hs). The strut location from the nozzle throat corresponded to 33%, 50%, 66.7% and 80% of the diverging length (Ld) of the nozzle. The schlieren images of the nozzle exhaust and nozzle internal wall pressure distribution from experiments were compared with the results from numerical simulation and the agreement was quite good. Computational results show that introduction of the strut caused a maximum total pressure loss of 1.5% at its maximum height. The calculations also show that 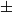 $ \pm $4
$ \pm $4 ${}^{\circ}$ thrust deflection angle could be achieved using combinations of strut location and strut height over a range of nozzle operational conditions. Thrust vectoring performance of strut insertion TVC was evaluated using a parameter called vectoring performance index (VPI) defined as thrust deflection angle per unit percentage of pressure loss. The maximum VPI was observed when xs=0.5Ld at
${}^{\circ}$ thrust deflection angle could be achieved using combinations of strut location and strut height over a range of nozzle operational conditions. Thrust vectoring performance of strut insertion TVC was evaluated using a parameter called vectoring performance index (VPI) defined as thrust deflection angle per unit percentage of pressure loss. The maximum VPI was observed when xs=0.5Ld at 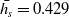 ${\bar{h_s}} = 0.429$ in both over-expansion and under-expansion conditions. The study reveals that an internal strut based TVC has a good future potential to be developed as an alternate TVC system obviating the requirement of carrying a fluid tank for a system like secondary injection TVC.
${\bar{h_s}} = 0.429$ in both over-expansion and under-expansion conditions. The study reveals that an internal strut based TVC has a good future potential to be developed as an alternate TVC system obviating the requirement of carrying a fluid tank for a system like secondary injection TVC.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Royal Aeronautical Society
References
- 1
- Cited by


