¹ See, for example, Dahl, Robert A., Who Governs? Democracy and Power in an American City (New Haven: Yale University Press, 1961)Google Scholar; Banfield, Edward C., Political Influence (New York: Free Press of Glencoe, 1961)Google Scholar; and Agger, Robert E., Goldrich, Daniel, and Swanson, Bert E., The Rulers and the Ruled: Political Power and Impotence in American Communities (New York: John Wiley & Sons, Inc., 1964).Google Scholar

² For an imaginative effort to develop a classification of generalized issue-areas relevant to different political systems, see Rosenau, James N., “Pre-theories and Theories of Foreign Policy,” in Farrell, R. Barry (ed.), Approaches to Comparative and International Politics (Evanston, Ill.: Northwestern University Press, 1966), pp. 27–96.Google Scholar See also Lowi, Theodore J., “American Business, Public Policy, Case Studies, and Political Theory,” World Politics, 16 (07 1964), 677–715.CrossRefGoogle Scholar

³ See White, Lancelot L., “Atomism, Structure and Form: A Report on the Natural Philosophy of Form,” in Kepes, Gyorgy (ed.), Structure in Art and in Science (New York: George Braziller, 1965), pp. 20–21 Google Scholar; and more generally, White, Lancelot L., Essay on Atomism: From Democritus to 1960 (New York: Harper and Row, 1963).Google Scholar

⁴ For some examples of the use of modern mathematics in the social sciences, see Kemeny, John G., “Mathematics Without Numbers,” Daedalus, 88 (Fall 1959), 577–591.Google Scholar

⁵ The Intelligence of Democracy: Decision Making through Mutual Adjustment (New York: Free Press of Glencoe, 1965), pp. 25–28.

⁶ See Copi, Irving M., Introduction to Logic (New York: Macmillan Company, 1953), pp. 100–105.Google Scholar

⁷ This verbal explanation of a mathematical theorem does not, of course, constitute a formal proof. Instead of encumbering the exposition of the analysis which follows with mathematical derivations, I have endeavored wherever possible to give references where a rigorous treatment of relevant points can be found.

⁸ For a review of some of the recent literature on “cluster seeking techniques,” see Ball, Geoffrey H., “Data Analysis in the Social Sciences: What about the Details?,” Proceedings—Fall Joint Computer Conference, 1965, pp. 533–559 Google Scholar; also, Alker, Hayward R. Jr., “Statistics and Politics: The Need for Causal Data Analysis” (Paper presented at the Annual Meeting of the American Political Science Association, Sept. 5–8, 1967, Chicago).Google Scholar

⁹ Johnson, Stephen C., “Hierarchical Clustering Schemes,” Psychometrika, 32 (09 1967), p. 242.CrossRefGoogle ScholarPubMed I am indebted to Rudolph J. Rummel for this reference.

¹⁰ A formal definition of a closed sequence and cycle in the theory of directed graphs (digraphs) is given in Harary, Frank, Norman, Robert Z., and Cartwright, Dorwin, Structural Models: An Introduction to the Theory of Directed Graphs (New York: John Wiley & Sons, Inc., 1965), pp. 40–41.Google Scholar The remainder of the analysis is devoted to showing how a digraph can be behaviorally coordinated with, or serve as a model of, a simplified political system.

¹¹ Since the construction of mutual influence sets is equivalent to the condensation of points of a digraph with respect to its strong components (with the mutual influence sets points of the condensation), the construction is unique. See ibid., p. 55, Theorem 3.2.

¹² Cf. this concept of concentration with the concept of evenness, or lack of concentration, of a nation's transaction flows in my “Trade in the North Atlantic Area: An Approach to the Analysis of Transformations in a System,” Peace Research Society: Papers, VI (1967), pp. 149–152. Another related concept is that of cosmopolitanism in my “A Note on the Cosmopolitanism of World Regions,” Journal of Peace Research, 1968, No. 1, pp 87–95.

¹³ Presumably, this condition will hold in most political systems of interest.

¹⁴ Decision-maker j's exclusion suggests that we should not count j in NT, the denominator of the PC index, because he is not directly or indirectly influenced by the minority control set, {a, m}. Accordingly, we define a revised power concentration index,

where

N_U = the number of decision-makers (not in minority control sets) uninfluenced by any minority control set.

PC′ is the same as PC for the hierarchical and mixed systems (because N_U = 0 for these systems), but PCȲ (=.83) is slightly less than PC(=.85) for the mutual adjustment system.

¹⁵ A system in which all influence relationships are asymmetrical and never flow “upward” can also be described as one in which (1) a decision-maker cannot be both the superior and subordinate of another, and (2) a subordinate of a subordinate is a subordinate. A necessary and sufficient condition for these requirements to hold is that the digraph of the system be free of cycles. See Kemeny, John G. and Snell, J. Laurie, Mathematical Models in the Social Sciences (New York: Blaisdell Publishing Company, 1962), pp. 103–104.Google Scholar

¹⁶ If there is more than one directed line be tween two mutual influence or minority control sets, which is not the case in any of the Lindblom systems, only one is preserved. Some of the consequences of this simplification for the PC index are discussed in Footnote 23, where a refinement in the index is suggested.

¹⁷ Harary, Norman, and Cartwright, op. cit., p. 270, Theorem 10.2.

¹⁸ Brams, Steven J., “DECOMP: A Computer Program for the Condensation of a Directed Graph and the Hierarchical Ordering of Its Strong Components,” Behavioral Science, forthcoming.Google Scholar A write-up and source deck of this program are available from the Syracuse University Computing Center, Syracuse, N. Y.

¹⁹ In digraph theory, the set of points with out going but no incoming directed lines at all levels (but the lowest) of the reduced digraph—the originators of influence in the system—is the unique point basis of the reduced digraph. In the original digraph (containing cycles), a point basis is not unique and will consist of one member from each of the originator mutual influence and/or minority control sets. See Harary, Norman, and Cartwright, op. cit., pp. 85–89.

²⁰ Ibid., p. 276.

²¹ Such “linking pins,” when operating at different hierarchical levels, have been found to perform a valuable integrative function in an organization. See Likert, Rensis, New Patterns of Management (New York: McGraw-Hill Book Company, Inc., 1961), ch. 8.Google Scholar In digraph theory, linkage decision-makers b and c. in Figure 5 are cut points whose removal would reduce the strength of connectedness of the digraph. See Harary, Norman, and Cartwright, op. cit., ch. 8. For a method to identify “liaison persons” in symmetric graphs, see Ross, Ian C. and Harary, Frank, “Identification of the Liaison Persons of an Organization Using the Structure Matrix,” Management Science, 1 (04-07 1955), 251–258.CrossRefGoogle Scholar

²² See French, John R. P. Jr., “A Formal Theory of Social Power,” in Cartwright, Dorwin and Zander, Alvin (eds.), Group Dynamics: Research and Theory (2nd ed.; New York: Harper and Row, 1960), pp. 727–744 Google Scholar; and Harary, Frank, “A Criterion for Unanimity in French's Theory of Social Power,” in Cartwright, Dorwin (ed.), Studies in Social Power (Ann Arbor, Michigan: Research Center for Group Dynamics, University of Michigan, 1959), pp. 168–182.Google Scholar

²³ Another elementary concept, influence relationship sets, might be usefully employed to build greater precision into the power concentration index. These sets would consist of all asymmetrical influence relationships occurring between each minority control set and the set or sets which it influences. For example, the values of the PC index for the three-actor systems pictured below are the same (.67), but the influence

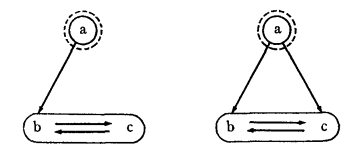
relationship set for the system on the left has one member (one directed line from the minority control set to the mutual influence set) while the influence relationships set for the system on the right has two members (two directed lines from the minority control set to the mutual influence set). Because minority control set {a} can exert direct influence on actor c in the right-hand system, a reasonable argument could be made to weight the influence of {a}, and the concentration of power in the system, by the number of members of the influence relationship sets. The more influence relationships which these sets contain, the more direct will be minority control—and, in one sense, the more concentrated power will be in the system.

²⁴ For experimental evidence on this point, see Jacob I. Hurwitz, Alvin Zander, and Bernard Hymovitch, “Some Effects of Power on the Relations Among Group Members,” in Cartwright and Zander, op. cit., pp. 800–809; Cohen, Arthur R., “Upward Communication in Experimentally Created Hierarchies,” Human Relations, 11 (Feb. 1958), 41–53 CrossRefGoogle Scholar; and Watson, David L., “Effects of Certain Social Power Structures on Communication in Task-Oriented Groups,” Sociometry, 28 (09 1965), 322–336.CrossRefGoogle ScholarPubMed

²⁵ Thibaut, John W. and Kelley, Harold H., The Social Psychology of Groups (New York: John Wiley & Sons, Inc., 1959), p. 125.Google Scholar

²⁶ Deutsch, Karl W., The Nerves of Government: Models of Political Communication and Control (New York: Free Press of Glencoe, 1963), p. 111.Google Scholar

²⁷ Brzezinski, Zbigniew K., “The Organization of the Communist Camp,” in his The Soviet Bloc: Unity and Conflict (rev. ed.; New York: Frederick A. Praeger, 1961), pp. 445–479.Google Scholar

²⁸ For an actor-oriented measure of influence in dominance situations (system representable by a complete asymmetric digraph where each actor either dominates or is dominated by—but not both—every other actor), see Kemeny, John G., Snell, J. Laurie, and Thompson, Gerald, Introduction to Finite Mathematics (2nd ed.; Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1966), pp. 390–391.Google Scholar

²⁹ For an extended treatment of this idea, see McClelland, Charles A., Theory and the International System (New York: Macmillan Company, 1966), Ch. 3Google Scholar, In a reeent paper, McClelland has used digraph theory to study international crises. See his “The Beginning, Duration, and Abatement of International Crises: Comparisons in Two Conflict Areas,” in Hermann, Charles F. (ed.) International Crises Google Scholar, forthcoming.

³⁰ A bilateral meeting represents an occasion for the meeting of one pair of countries whereas a multilateral meeting represents an occasion for several pairs of countries to meet with each other. Brzeziński did not distinguish between the meetings of pairs of delegations in bilateral and multilateral meetings.

³¹ If we assumed six meetings per pair as the cutoff point in the second period (i.e., 54 percent above the expected number), then only 5 of the 28 pairs of countries would be in influence relationships and at least two of the eight countries would therefore not be in influence relationships with any others. At the five-meeting-per-pair cutoff point, on the other hand, 9 of the 28 pairs of countries are in influence relationships, and each of the eight countries is in an influence relationship with at least one other. In the first period, one country (Rumania) is not in an influence relationship with any other, but the three-meetings-per-pair cutoff point for this period cannot be lowered without violating the criterion that the cutoff point be greater than the expected number of visits per pair for the system.

³² The eight countries, and their code abbreviations, are: Bulgaria—BUL; China—CHN; Czechoslovakia—CZE; East Germany—GME; Hungary—HUN; Poland—POL; Rumania— RUM; and Soviet Union—USR.

³³ See, for example, McNeal, Robert H. (ed.), International Relations Among Communists (Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1967), pp. 76–78.Google Scholar

³⁴ For a discussion of these points, see Brzezinski, op. cit., pp. 482–483.

³⁵ Cf. Biker's argument for n-adic, rather than dyadic, definitions of power. William H. Riker, “Some Ambiguities in the Notion of Power,” this Review, 58 (June, 1964), 341–349.

³⁶ Kluckhohn, Clyde, “Cultural Anthropology,” in White, Lynn Jr. (ed.), Frontiers of Knowledge in the Study of Man (New York: Harper and Brothers, 1956), p. 39.Google Scholar

³⁷ See Alexander, Christopher, Notes on the Synthesis of Form (Cambridge, Mass.: Harvard University Press, 1964), p. 194 Google Scholar, Footnote 12. It should be noted that the non-numerical digraph model was used to formulate the numerical PC(m,n) index.

³⁸ See Carnap, Rudolph, “Elementary and Abstract Terms,” in Danto, Arthur and Morgenbesser, Sidney (eds.), Philosophy of Science (Cleveland: World Publishing Company, 1960), p. 155.Google Scholar The above analytic (nonfactual) statement illustrates the great advantage of translating an already developed mathematical theory into a mathematical model of a political system: the model inherits from the theory a stock of proven theorems with a logically unassailable theoretical structure.

³⁹ Carl G. Hempel, “Operationism, Observaion, and Theoretical Terms,” ibid., pp. 117–120.

⁴⁰ Retroduction, which involves reasoning back from diverse phenomena to a pattern within which they appear intelligible, should be distinguished from induction, which involves the discovery of regularities (empirical correlations) in repetitive observations of details in phenomena. See Hanson, Norwood R., Patterns of Discovery: An Inquiry into the Conceptual Foundations of Science (Cambridge, Eng.: Cambridge University Press, 1958), pp. 85ff.Google Scholar I am indebted to Wayne A. Kimmel for this reference.

⁴¹ This is not to say that study of the isolated parts of systems is not useful but rather that we must also direct our attention to ways of putting the parts together into a palpable whole. This point is developed more fully in my “Transaction Flows in the International System,” this Review, 60 (Dec. 1966), 880–881. For a discussion of these contemporary approaches in biology, see Waddington, C. H., The Nature of Life (London: George Allen & Unwin Ltd., 1961), esp. pp. 21–24.Google Scholar

⁴² Bronowski, Jacob, “The Discovery of Form,” in Kepes, , op. cit., esp. pp. 56, 59–60.Google Scholar

⁴³ MeLuhan, Marshall, The Gutenberg Galaxy: The Making of Typographic Man (Toronto: University of Toronto Press, 1962), p. 252.Google Scholar

⁴⁴ On this point, see Barber, James D., Power in Committees: An Experiment in the Government Process (Chicago: Rand McNally & Company, 1966), p. 129.Google Scholar

⁴⁵ For an analysis of changes in the structure of influence relationships over time based on visits between heads-of-state and other high-level officials for all nations in the world in 1964–65, see Brams, Steven J., “The Structure of Influence Relationships in the International System,” in Rosenau, James N. (ed.), International Politics and Foreign Policy: A Reader in Research and Theory (rev. ed.; New York: Free Press, forthcoming 1969).Google Scholar In ibid., it is suggested that the kind of influence tapped by data on international visits tends to reflect the visited nation's control over broad policy areas, but not specific actions related to the vital national interests, of the visiting nation.

⁴⁶ One concept making use of interaction data that has been of particular interest in the structural analysis of organizations is status. See Katz, Leo, “A New Status Index Derived from Sociometrie Analysis,” in Moreno, J. L. (ed.), The Sociometry Reader (Glencoe, Ill.: Free Press of Glencoe, 1960), pp. 266–271 Google Scholar; and Harary, Frank, “Status and Contra-status,” Sociometry, 22 (03 1959), 23–43.CrossRefGoogle Scholar

⁴⁷ Dahl, op. cit.

⁴⁸ Banfield, op. cit.

⁴⁹ Haas, Ernst B., The Uniting of Europe: Political, Social, and Economical Forces, 1950–1957. (London: Stevens & Sons, 1958).Google Scholar

⁵⁰ Deutsch, op. cit., p. 253.

⁵¹ One kind of algebraic ordering which has been proposed as a model for the structure of cities and organizations is the semilattice. See Alexander, Christopher, “A City is Not a Tree,” Architectural Forum, 122 (2 parts; 04, May 1965), pp. 58–62, 58–61Google Scholar; and Friedell, Morris R., “Organizations as Semilattices,” American Sociological Review, 32 (Feb. 1967), 46–54.CrossRefGoogle Scholar

⁵² Bavelas, Alex, “Communication Patterns in Task-oriented Groups,” in Cartwright, and Zander, , op. cit., pp. 669–682.Google Scholar At a more theoretical level, see Hopkins, Terence K., The Exercise of Influence in Small Groups (Totowa, N. J.: Bedminister Press, 1964).Google Scholar

⁵³ For various measures of the “concentration of authority” based on asymmetric dominance relationships between all pairs of actors in a system, see Bartos, Otomar J., Simple Models of Group Behavior (New York: Columbia University Press, 1967), pp. 56–61.Google Scholar These measures, like Russett's, are algebraic in nature and do not presuppose a decomposition that depicts the geometric order in a system.