INTRODUCTION
Despite much weakening of the sovereignty norm over the last decades, there is one area where this norm remains very powerful: there is widespread consensus that foreigners should not interfere or intervene in the democratic elections of another country, unless possibly to support the democratic process. However, this norm is observed mainly in the breach. According to a new dataset, actions by outsiders to support a candidate running for elections are observed in one-third of all elections in the world.Footnote 1
In this paper, we outline the conceptual distinction between processes, the “how” of elections, and parties competing in them, the “who” of elections. We then use this distinction to develop a theory of electoral intervention. The theory is built on a formal model of elections with bias. Domestic parties compete for office using their resources and popularity; whether they win or not is a function of the institutional rules of the game. Outsiders have a choice of investing in the how, the who, or both. Outside actors care, to a degree that varies, about cleaner (more legitimate) contests and about the policy platform of the prospective leaders.
The primary contribution we make is theory building. Neither the possibility of links between processes and candidates nor the existence of such a distinction have been studied. The model produces predictions on three quantities of interest: the amount and mix of resources invested by the outsider in the election, incumbent win or loss, and the degree of fraud (or compliance with democratic rules). Some of the comparative statics can better illuminate cases that so far have been puzzling. Others represent novel testable implications. We present some preliminary evidence, illustrating the patterns predicted by the theory.
A key insight we seek to convey is that outsiders’ interest in elections of other countries can be conceived of as a mixture of two types of concerns: geopolitics and democratic liberalism. Concern with geopolitics motivates investment in candidates: this investment grows as the country’s viable candidates grow further apart. Concern with liberalism motivates investment in fair contests.
Notably, a “cleaner” contest changes the probability of specific candidates to win, feeding into the geopolitical calculations of the intervener. This makes investments in candidates and processes mutually dependent. The observation that clean contests imply a different probability of winning—for incumbent and opposition—is not new by itself.Footnote 2 We formalize it, alongside partisan concerns by the outsiders for government or opposition to win, and demonstrate a number of nontrivial implications.
For example, we can explain why nondemocratic states, such as Qatar, would invest in democracy promotion during the Arab spring.Footnote 3 Instead of viewing such behavior as an insincere aberration, we show that it may be a sensible strategy. Because investing in fair elections helps support for the friendly opposition parties to go farther, democracy promotion is an optimal strategy even for a state that attaches no intrinsic value to fair elections.
Our argument can readily explain a neglected, yet prominent aspect of foreign interventions in elections: namely that, historically, outside powers have often relied on a mix of interventions. We show why outside powers would not invest exclusively in one strategy, i.e., the “how” or the “who” in elections. If the friendly party is in opposition, investing both in a fair election and in more domestic appeal for the opposition is optimal for the foreigners. An outsider that prizes clean elections would invest in fairer rules of the game in a country governed by a friendly incumbent, while using candidate interventions to offset possible electoral losses of the incumbent.
Election interventions often entail cases where different powers are intervening on different sides: for the government or the opposition (Risse and Babayan Reference Risse and Babayan2015; Tolstrup Reference Tolstrup2009). We call these situations “election wars.” Existing studies do not distinguish between process-based and candidate-based intervention strategies. Nor do they allow for the strategic adjustment of the behavior of one power in anticipation of the response of another power. Among other things, it is not readily obvious in such cases whether a liberally inclined foreign power would respond to the entry of an illiberally minded foreign competitor (“black knight”) by increasing or by decreasing investment in the democratic process.
Our model allows the possibility to study these puzzles. Take as a starting point the case of a liberal hegemon, e.g., the United States, intervening, but consider adding a second—illiberal—intervener to the contest. As the stakes for one power increase (meaning the importance of the election), its candidate does better. When it comes to election quality, there is a twist. If the liberal power likes the opposition, increasing stakes lead to higher investment in candidates and processes, and we have cleaner elections. If the liberal power likes the incumbent, higher stakes increase candidate support, but, at first, lead to less investment in a fair contest. The same holds true for the illiberal power. In this case we might even see a deterioration of democratic standards compared to their level before the intervention.Footnote 4
Thus, contrary to what the literature suggests (Donno Reference Donno2013; Kavakli and Kuhn Reference Kavakli and Kuhn2016), rising geopolitical importance of a target state is not always bad for democracy. Whether it is or is not depends on whether the intervener is liberal, on whether it faces a challenger, and whether there is polarization in the policy positions of the government and opposition.
We extend our model in two directions of interest. In one extension, we allow outside powers the option of dispensing with democracy altogether via a coup. We show that increased domestic polarization leads outsiders to abandon election interventions in favor of coups. In another extension, we allow for parties to change their positions in order to attract support from outside patrons. We also demonstrate the conditions under which the latter occurs and the implications for policy polarization.
We contribute to work on elections and democracy. Formal models of elections have been used to try to understand the timing and role of elections as tools of accountability (Fearon Reference Fearon2011). Lately, scholars have applied them to the study of illiberal contests (Gehlbach and Simpser Reference Gehlbach and Simpser2015; Little Reference Little2012; Rundlett and Svolik Reference Rundlett and Svolik2016), including those in autocracies (Lorentzen Reference Lorentzen2013; Shih Reference Shih2013). We introduce the role of outside actors. While we model the effects of intervention on electoral integrity, our work has implications for scholarship on the diffusion of democracy (Gleditsch and Ward Reference Gleditsch and Ward2006). We help identify the power distributions in world affairs most likely to further democratization.
Our model also allows us to study issues such as how the wealthy influence elections, the role of donors for promoting policy agendas in American states, and how foundations fuel change and backlash.Footnote 5 The approach is adaptable to the study of interventions in democracy by different actors, subnationally as well as cross-nationally.
THE WHO AND THE HOW OF ELECTIONS: A THEORY WITH INTERESTED OUTSIDERS
Outsiders have a long and illustrious history of casting a “silent ballot” in other countries’ elections (Forster Reference Forster1963). This attitude was summarized in an infamous Pravda editorial. On the eve of the 1945 Finnish elections, the Soviet daily upended the conventional view of the matter when it wrote that “elections are not to be considered internal affairs” for the countries holding them. Soviet Russia, which controlled some Finnish territory, exerted considerable influence in the election. Its main objective was to remove anti-Soviet ministers—elected in 1939—who led Finland into war with Soviet Russia. The USSR accused some of the ministers of supporting fascism. It also demanded the dissolution of the Finnish veterans’ association, “Comrades in Arms,” because it believed that the 400,000-plus members would sway the outcome in favor of anti-Soviet parties. Moscow sought to bolster support for the Democratic People’s Union (SKDL), which included the Communist Party, and it publicly worried that the elections may be biased against leftist parties. Friendly relations with the Soviet Union, however, were critical at the time because Finland owed the USSR $300,000,000 in war reparations. In statements issued before the election, the Soviets made it clear that financial support for Finland, and even its territorial integrity, depended on the electoral outcome. The elections were free of fraud, and Soviet Russia’s party allies performed well.
Elsewhere in Europe, Soviet behavior showed variation. In the Polish elections of 1947, the Soviets helped the government bludgeon its way to victory. The political police recruited, for example, almost half of the electoral commission’s members. About eighty thousand people—members and suspected supporters of the noncommunist People’s party (PSL)—were arrested during the election period. Polling stations were also controlled by the militia and the army. Pro-opposition activists were intimidated and sometimes murdered; many other voters were forced to vote in public.Footnote 6
This type of election-related activism is hardly reserved to the Soviet Union, or the early Cold War. To take a more recent example, European leaders publicly urged the Bosnian electorate to vote for pro-EU candidates in the presidential and general elections in Bosnia-Herzegovina on October 3, 2010. British and German foreign ministers William Hague and Guido Westerwelle said in an open letter, “Our message to the Bosnian people is that our countries are sincere in wanting to help and support you, but for that to be successful we need leaders who choose to work with us towards the goal of EU integration.”Footnote 7
These cases show outside powers spending resources to either impede or improve the process of voting. They also show outsiders aiming to help a partisan ticket by extending resources to help the party appeal to voters. Understanding these phenomena, and what they imply for electoral integrity, is important. We proceed to outline a theory that clearly lays out the stakes, actors, and set of available choices.
A Model of Outside Interventions in Biased Elections
We start with a simple model. We conceive of elections as manipulated contests (Gandhi and Przeworski Reference Gandhi and Przeworski2009), where manipulation varies along a continuum from low to high (Hyde and Marinov Reference Hyde and Marinov2012). For simplicity, we focus on elections in which the incumbent leader (or incumbent political party) is running, the opposition is challenging the incumbent, and if the incumbent loses, the opposition assumes power.
Elections
The outcome of an election is determined by the support among the voters for a certain candidate. There is some vote share χ that the incumbent party would receive if elections were entirely free and fair. Let χ be the support of a candidate, where 0 ⩽ χ ⩽ 1. Absent any distortion such as an unfair advantage to one of the parties the outcome of the election is determined by the mapping f(χ) = χ.
Bias
In recent years, there has been an explosion of work on the various ways in which democratic elections can become less democratic (Alvarez, Hall, and Hyde Reference Alvarez, Hall and Hyde2008; Schedler Reference Schedler2002). Scholars and practitioners have introduced the concept of electoral integrity: a series of (universal) benchmarks that democratic elections must meet (Norris Reference Norris2015). These include voter registration laws, election procedures, district boundaries, how the vote count is conducted, and many others. While the collection and weighting of indicators remains a matter of debate, we borrow a simple insight from existing work. The democratic ideal is obtained when a contest is held under rules that bestow no special advantage to any candidate running in the election. Where electoral rules are without flaws, observed vote share is most likely to reflect the true support of candidates. As rules become less perfect, elections deviate more and more from the democratic paradigm. Usually this deviation has a particular beneficiary and can be represented as bias, or asymmetric advantages. These usually favor the incumbent (office-holding) candidate or party in the contest. We assume that the bias always favors incumbents. Our model, however, can be adapted to study alternative cases where the bias favors the opposition in some elections or does not benefit a particular party.
We formalize bias by uncoupling the final vote share in an election from the true support for a candidate. Let β measure the election’s bias in favor of the incumbent. We observe vote share; true incumbent support χ is unobserved. So far, outside intervention of any kind is absent.
Interventions
We define an electoral intervention as a deliberate attempt by a foreign government to change the electoral rules or the appeal of the candidates. We distinguish between pre-election interventions (e.g., which include helping with election campaigns, threatening voters with consequences, insisting on a fair vote) and postelection interventions (e.g., seeking to overturn the results of the elections, making the results stick, or altering the composition of the elected government). In this project, we focus on pre-election interventions. By pre-election, we mean everything before the aftermath of voting. We include the counting of ballots, aggregation, and announcement of results. Empirically, many interventions occur pre-election. This distinction would allow future work to study the logic of postelection decisions separately.Footnote 8
We next distinguish between two different types of interventions—candidate interventions and process interventions. We assume that incumbent vote support can be moved away from χ by offering support c for that candidate. We choose the bias β to be a function of some choice argument p, the process intervention a foreign power can undertake. We will also assume that the incumbent benefits when c > 0 (the opposition benefits when c < 0), and a fairer process results if p > 0 (bias grows if p < 0).
Examples of candidate interventions would be outsiders conditioning financial transfers to a country on who wins, or threatening to invade if the “wrong” ticket won, or threatening to expel guest workers that are citizens of the target country. Sometimes, economic sanctions amount to procandidate interventions (Marinov Reference Marinov2005, 566–7). Outsiders can also sponsor elements of a candidate’s campaign (e.g., paying for a band of singers to promote a candidate or airing procandidate messages on TV channels, as Russia did during the 2004 Ukrainian elections). Another example is the signing of agreements and trade/aid deals close to an election, thus creating the impression of support for the current incumbent. A country could also hand an incumbent government a diplomatic victory, as Portugal did for Kaunda in the Zambian presidential elections of 1968.Footnote 9
Examples of process interventions include paying for election observation and for the organization of elections, conditioning aid on the execution of free and fair elections or threatening sanctions over fraud (Galtung Reference Galtung1967), calling for the repeal of discriminatory legislative acts,Footnote 10 paying to train political parties in democratic practices. To take one example of the latter, consider a Morocco-targeted program by the National Democratic Institute (NDI) and the International Republican Institute (IRI), funded by USAID, the National Endowment for Democracy (NED), and the State Department’s Middle East Partnership Initiative (MEPI). This program comprised 17 separate projects from 2003 to 2010, with time frames ranging from three months to two years and funding from $110,000 to $2,470,000. Project activities focused on strengthening political parties, supporting election-related activities, increasing the participation of women and youth, and strengthening locally elected officials and parliament, for a total program cost of $12,255,699.Footnote 11 A different kind of process intervention occurred in 2007 in Bosnia. Under international pressure, campaign financing was regulated for the first time, by enforcing disclosure of donations and stipulating limits.
We should emphasize that a country can engage in more than one type of intervention at the same time—investing in candidates and processes. Finally, we do not require investments to be very effective at achieving their goals.Footnote 12 We say more about this later.
Formally, the election result becomes a function of the ex ante level of bias and the ex ante level of support, which are now affected by the investment in candidates and processes: f(χ(c), β(p)) = f(c, p).
(Geo)political Concerns
The foreign power cares about the position of the incumbent on the political spectrum (Agov ) and about the position of the opposition (Bopp ).Footnote 13 Since divisions between domestic factions are important for our argument, we pause to offer some examples.
According to Thucydides, democratic politics in early Hellas featured divisions on whether to ally with Sparta or Argos (Robert Stressler 1998). Both powers were keenly aware of the need for allies, and sought to influence the politics of Greek city states in order to install allies in office. Little has changed since then. Imperial Russia and the Soviet Union have always been interested in a belt of friendly states in Eastern Europe.Footnote 14 In some ways, this is the Russian version of the “Monroe” doctrine the United States implemented toward Latin America. Friendly states may permit Russian bases. Friendly neighbors are also more likely to accept Russian goods and welcome investment in key value-adding areas, such as nuclear energy.
Apart from their geostrategic objectives, sometimes what foreign powers find objectionable abroad is more closely related to nationalism and ethnic intolerance. Elections in the successor states of former Yugoslavia often placed in office candidates with questionable commitment to ethnic peace and reconciliation. Foreigners clearly worried about the ability of democracy to moderate the positions of winning candidates in the Western Balkans. Biliana Plavšić’s loss in the 1998 elections in Republika Srpska came after she had adopted very pro-U.S. positions and was characterized as the “United States’ running mate.”Footnote 15 China frets over politicians with pro-independence agendas in Taiwan.
When parties in a democracy have diverging policy positions, elections determine the relative probability these positions will result in future policy. Within the context of our model, this probability can be influenced by investment in processes and candidates.
The foreign power’s level of concern with positions may vary across countries. We define a parameter Γ ⩾ 0 that represents a country’s geopolitical importance from the perspective of an outside power. A high value would, for example, be more appropriate for former colonies, for countries hosting a military base, or for countries with ethnic diasporas the intervener cares about. Higher values of the parameter Γ indicate that the difference between party positions is more consequential.
This leads us to the first component of a foreign power’s utility function:
$$\begin{equation*}
u^\diamond = \Gamma \Big [ f(c,p) \times A_{gov} + [ 1-f(c,p)] \times B_{opp} \Big ].
\end{equation*}$$
Liberal Concerns
Research in international relations and political theory suggests that actors in world affairs may care about democracy. The possible reasons are many. They include Kantian considerations, which posit that democracies share values with each other—including pacific values (Russett Reference Russett1993). They also include considerations related to human rights (Sen Reference Sen2000) and sustained economic growth, as well as models of development (Narizny Reference Narizny2007). We do not seek to explain why some states may care about democracy. We simply allow this concern to vary.
A simple way to capture a power’s commitment to liberalism is to introduce a parameter Λ. The term Λ is a reduced-form representation of the types of institutional, long-run benefits a state may anticipate to arise from more democracy in another country.
We distinguish between liberal, aliberal, and illiberal powers.
For liberal powers, we assume Λ > 0. Such states gain from democracy in another state.
We call states with Λ = 0 aliberal actors: they take no sustained interest in the existence or lack of stronger rules for the democratic game abroad. It is a plausible conjecture to place Qatar, and possibly China, in this category.
By contrast, Λ < 0 represents illiberal states: countries that define their interests as poorly served by strong democratic institutions abroad. Putin-led Russia may be an example of such a power.
We add a word of caution. We do not assume that a country’s observed actions vis-à-vis another country’s elections will always reflect the sender country’s genuine concern with liberalism abroad. In fact, we will show that strategic considerations may elicit democracy-promotion strategies from states that are indifferent to democracy and depress such impulses in otherwise liberally inclined powers.
In our model, outside interventions in processes p affect the bias β. The outsider has an additional term in the utility function:
$$\begin{equation*}
u^{\diamond \diamond } = - \Lambda \beta (p).
\end{equation*}$$
This term basically says that any investment p > 0 in bias reduction has an (intrinsic) positive effect for the liberally minded power. We assume that investment in fairer rules of the game is an investment in institutions. Such investment will not necessarily make the target country an exemplary democracy, but it will bring the outcome closer to this ideal.
Cost Structure
When outsiders intervene, they pay a price. Fielding election observers and paying for better ballot-counting equipment, for example, are costly. Diplomatic maneuvering thus requires commitment and carries opportunity costs. In the 2010 election in Burundi, the opposition withdrew from the election due to allegations of fraud and violence in the weeks before the election. Member states of the East African Community (EAC)—Rwanda, Kenya, Uganda, and Tanzania—where Burundi is also a member, visited Burundi and urged the opposition parties not to boycott the elections in order to prevent postelection violence.Footnote 16 Aiding the campaign of a candidate is costly.
Costs can go beyond (expected) expenditure and can be defined in a very broad sense. They might entail the reduction of domestic support for the intervener, at home and in the target country—and in terms of lost support in the international community.
We assume that c and p are costly, regardless of whether they work for or against the incumbent, and whether they foster democracy or go against it. The third part of the outsider’s utility function, therefore, consists of two quadratic cost terms:
$$\begin{equation*}
u^{\diamond \diamond \diamond } = - c^2 - p^2.
\end{equation*}$$
The Intervener’s Problem
Gathering all terms, this is the utility function of the foreign power:
$$\begin{eqnarray*}
u_{int} &=& \Gamma \lbrace \ f(c,p) \times A_{gov} + [ 1-f(c,p)] \times B_{opp} \rbrace \\
&& -\, \Lambda \beta (p) - c^2 - p^2.
\end{eqnarray*}$$
We look at two broad, substantively important scenarios of interest (Figure 1): the case where one power is intervening vs. the case in which it faces an opposing actor.
FIGURE 1. The Intervention Problem
We call the one-power problem the election hegemon scenario. We speak of a “(regional) hegemon” if there is no other influencer present. U.S. intervention in Bolivia or the Philippines, or British intervention in Guyana are examples. “Hegemon” refers to a single intervener (or a coalition of similarly minded actors), whereas “regional” adds to this the regional proximity of the target of interventions. In such cases, policy in target would matter a lot to the intervener (Γ is high). We call election wars cases where two powers, such as the United States and Russia may intervene on opposing sides, as they have done in Ukraine. Interveners are typically large states with substantial resources. If not, their budget limitations would constrain behavior (cf. Appendix Formal Solution of the Constrained Optimization Problem).
Domestic Conditions
Domestic conditions in the target state are captured, in a stylized form, by incumbent support χ, the measure of bias b, and the policy positions of government Agov and opposition Bopp . These parameters enter the optimization problem of the intervener(s). We can also accommodate cost structures for the two types of electoral interventions, c and p, that differ among countries. We look at cases when investing in p is not feasible or ineffective—as would be the case in a consolidated democracy or against unwilling incumbents. We do the same for candidate investment c, which could be unwelcomed or could backfire. Our model applies primarily to recipient countries that are democratizing, but should also be relevant for countries with strong institutions.
MODEL PREDICTIONS
While the single-intervener case is only a decision-theoretic problem, its predictions merit some discussion because they illustrate the basic mechanisms at work in our model. This facilitates the transition to the election war case.
Before we begin, we further simplify our model by introducing the concept of political polarization. Maximizing uint is equivalent to the following maximization problem:
$$\begin{equation*}
\max\limits_{c,p} \pi \Gamma f(c,p) -\Lambda \beta (p) - c^2 - p^2.
\end{equation*}$$
The polarization parameter π = Agov − Bopp measures the difference between the positions of the government and the opposition from the point of view of the outsider.Footnote 17 A positive π implies the incumbent is preferable and a negative π implies the opposition is preferable.
We choose a simple linear effect of the bias β on the election result f(χ, β) = χ + β. Absent any form of foreign intervention, a parameter value of β = 0.15 indicates an increase in the vote share by 15 percentage points at any level of support χ.
We show predictions based on a workhorse model, where we use
$$\begin{equation*}
f(c,p)=\chi + c + \left(\sqrt{b}-p\right)\left(\sqrt{b}-c\right)
\end{equation*}$$
for the vote share (the election result) and
$\beta (p)=b-\sqrt{b}p$
for the resulting bias at c = 0.Footnote
18
Before we present the main predictions of our model, we offer some notes on the main assumptions built into the model and the functional form. First, we should note that investment in candidates c directly affects the odds of victory, whereas investment in p is more complex—affecting who wins, but also the rules of game. The starting point of our theoretical model is a simple premise: any reduction in the bias of an election will affect the final vote count.
Second, we argue that foreign powers will often invest in candidates and processes simultaneously. In our model this is implied by the quadratic cost functions, which produce an interior solution for suitable parameter choices. This is motivated by the empirical phenomenon of increasing marginal costs (or, alternatively, diminishing returns) for specific actions or policies. Trying to achieve a marginal increase in the vote share (e.g., by increasing the turnout of the core supporters of a candidate) might be cheap at first but trying to influence large swaths of the population will become increasingly expensive.
Third, we propose a way in which investments in processes and candidates are mutually related and assume that the cost of a reduction of the bias depends on its initial level. Formally, a decrease in the bias makes the mapping between the support for a certain candidate within the electorate and the final vote share more immediate. The cost of a reduction of the bias by a certain amount depends on the initial level of the bias. This is intuitive: starting from a high bias (e.g., irregularities in the ballot counting process), reduction is less costly since better compliance could be enforced more easily (e.g., through election observers and threats of cutting aid). If the initial bias is already quite low, further improvements are more costly. For example, reducing gerrymandering or reforming campaign finance are more difficult to achieve for an outside power.
By the same token, deterioration of the voting standards (through election fraud) that start from a fair process is assumed to be more costly than improving/deteriorating voting standards in an already biased process. An additional property of our specification is the positive effect of a bias reduction on the effectiveness of candidate support. A decrease in the bias (i.e., a positive investment in p) enhances the effect of any investment in candidate support c on the final vote share. Suppose that a foreign power promises aid to the country in case of opposition win. The voters should learn of this promise in order for it to be effective for garnering votes. It follows that the foreign power should pressure the government into providing enough freedom and media access to the opposition for the message to get across.Footnote 19
The interaction between c and p implied by the functional form gives an additional incentive to use both means of support. But even if we would use
$f(c,p)=\chi + c + \left(b-\sqrt{b}p\right)$
foreign powers would still use both—candidate and process support—if we use convex costs functions. Under alternative specifications one would find a mix between investment in c and p under a wide variety of sensible assumptions (assuming diminishing returns, some form of increasing marginal costs, etc.).Footnote
20
The Hegemon Case
For the model predictions, we solveFootnote 21 the maximization problem:
$$\begin{eqnarray*}
&&\max _{c,p} \pi \Gamma \left[\chi + c + \left(\sqrt{b}-p\right)\left(\sqrt{b}-c\right)\right]\\
&&\quad -\, \Lambda \left(b-\sqrt{b}p\right)-c^2-p^2.
\end{eqnarray*}$$
Figure 2 shows analytical solutions for a set of reasonable parameter choices. This will be our basic, or “work-horse” specification: other hegemonies change some parameters, and, in our election war cases, the power with these parameters faces off another power.
FIGURE 2. Optimal Choices c* and p* in (Liberal) Hegemony
We use an initial parametrization of Γ = 0.75 (i.e., target country is important) and Λ = 0.5 (i.e., liberalism matters to the outsiders). We assume (here and in what follows) that the true support is at χ = 0.5 and that there exists an ex ante bias of b = 0.15. Keeping those parameters in mind is important, since they provide a comparison with the nonintervention case: an incumbent win with a vote share of f = 0.65, where 0.15 is from undue advantages. Outside intervention changes this counterfactual, or status quo, outcome.Footnote 22
Figure 2 sheds light on the extent of and sources of partisan bias in democracy promotion.Footnote 23 Here, we compare our baseline case to the case where the geopolitical importance of the target country is reduced (Γ = 0.5, Figure 2b) and to the case where an outside power is aliberal (i.e., unconcerned about democracy; Λ = 0, Figure 3).
FIGURE 3. An Autocracy May Press for Election Integrity
The difference in the positions of the government and the opposition is going to predict the process/candidate mix, and the intensity of electoral interventions. This is true unless the country is geostrategically unimportant (Γ = 0). If the foreign intervener does not care about policy outcomes at all, then there will be no candidate intervention (c = 0) and democracy promotion p will be set according to the degree of liberal concerns Λ. The same outcome is observed when there is no difference in the policy positions of the government and the opposition (π = 0).
Thus, U.S. intervention in the Solomon Islands, a strategically unimportant country, would only be driven by a concern for liberalism. Also, in the Philippines, where “all five leading Presidential candidates are vying with one another to convince voters how much they love America and how much America loves them,”Footnote 24 our specification would predict that only process interventions would occur.
Predictions. As polarization increases (the intervener prefers the incumbent in power), interveners adopt less democracy promotion (lower p) and switch to progovernment candidate interventions (c > 0).Footnote 25
As the stakes for an intervener increase (i.e., an election becomes more consequential geopolitically, Figures 2b and 2a), we see more democracy promotion if its favored candidate is in opposition (π < 0) and less if it is in power (π > 0).Footnote 26 Thus, contrary to the view in the literature, geopolitical considerations do not always erode the commitment to promote free and fair elections.
A power that attaches no intrinsic value to strengthening democracy abroad would invest in strengthening or in eroding democracy conditional on what serves its candidate (Figure 3). The former occurs when the sender prefers the opposition, the latter, when the sender prefers the government. One mechanism for this result is the mutual dependence of c and p. An extra unit contributed to the campaign of a friendly party will purchase more influence if the election is cleaner. Russian concerns with clean elections in postwar Finland resonate with this concern. Soviet aid for the opposition—the Communist ticket—would buy more if the playing field was more even.
On the right-hand side of Figures 2a and 2b, we see that a liberal foreign power may choose to offset some of its investment in cleaner processes (which hurt the incumbent), by expending more money into candidate support for its favored party. For example, officials of the Mubarak regime in Egypt were consternated by the policy of the American government to aid prodemocracy groups, arguing that this undermined their control over power.Footnote 27 A policy of aiding the government via loans and aid, while investing in more democratic rules, may be an optimal mix. In fact, the regime may have received more candidate support to offset prodemocracy investments.
Budget
If we set a maximum amount of resources that could be spent on electoral interventions c 2 + p 2 ⩽ y, then this slightly alters the optimization problem of the election hegemon. A formal solution of this case can be found in the Appendix Formal Solution of the Constrained Optimization Problem. Whenever the budget constraint is binding, the election hegemon will spend her budget on c and p proportional to the desired mix of c* and p* in the absence of a budget constraint. A power with a small budget influences elections in a small way.
Vote Share and Bias as Hegemon Turns More Liberal
Arguably, over the last decades, the United States has become more committed to democracy. This motivates our next set of comparative statics. We illustrate how some quantities of interest are changed by a rise in liberal concerns from Λ = 0 to Λ = 0.5. We compare the outcomes of the scenario in Figure 2a with the scenario in Figure 3. Figure 4 demonstrates the impact on vote share and bias. We mark the nonintervention status quo outcome (SQ) as a reference point on how outsiders alter the domestic power game.
FIGURE 4. Outcomes of Election Hegemon Scenario
The changing mix of c and p interventions causes total expenditure to rise as concern with liberalism grows. This is in part a reflection of the fact that concern with liberalism justifies investment in the democratic processes. But, the effects are more subtle. In our model, investment in processes increases the payoff of investing in candidates, thereby increasing the amount spent on one’s favored party. This also means that we expect a counterintuitive effect: a rise in liberal concerns leads to more candidate interventions. An implication is that, after the end of the Cold War, we can expect more side-taking.
Predictions. Figure 4 shows that the growing importance of liberal norms reduces the vote share of the incumbent at any level of polarization (Figure 4a), primarily by reducing the unfair bias enjoyed by the government (Figure 4b). Still, if the foreign power likes the incumbent, due to offsetting candidate investment, this lower bias hardly hurts the vote tally.
Reducing the Effectiveness of Interventions
In consolidated democracies, the domestic rules of the game may be so strong that they cannot be easily undermined (or strengthened). Or, it may be the case that the target government refuses democracy promotion (as Iran would do to the United States), or accepts only a blunted, nonthreatening version (Bush Reference Bush2012). There might also be local actors that capture democratic aid, and undermine its intended effects (Jamal Reference Jamal2007). One way to model these concerns in our framework is to imagine that the investment in p becomes progressively less effective, until its impact is reduced to 0. The parameter ρ p ∈ [0, 1] captures the effectiveness of a unit investment in democracy.Footnote 28
We can do the same for candidate interventions. While the targeted candidate always wins additional votes from increased spending towards her campaign, there might be other reasons (outside the realm of our model) that prevent her from receiving support from a foreign intervener. One possibility is concern for corrupt allocation of finances or concern for nationalist backlash. Thus, the effectiveness of c may converge toward 0 (again, variation in effectiveness can be captured by a parameter ρ c ∈ [0, 1]).Footnote 29
Predictions. Figure 5a shows us the impact of reducing the effectiveness of c. Due to the missing interaction of investment in processes p and candidates c, we see that the foreign power will actually invest weakly less into democratization if candidate support is ineffective (Figure 5a). Overall, prohibiting candidate support makes electoral intervention much more costly for the election hegemon since she can only influence the result by a change in the rules.Footnote 30 This decreases the effect of polarization in the target country on the final vote share of the election.
FIGURE 5. Changing the Scope of Intervention (Liberal Hegemon)
Figure 5b is another illustration of the interaction between p and c: positive investment in p gives the electoral hegemon an incentive to invest more (in absolute value) in candidates. If we set p = 0, the liberal hegemon will invest weakly less in candidates (in absolute values), because there is no additional “boost” through candidate support.
While they might be motivated by different concerns, there is a mutually enforcing relationship between the two of them. For the election war scenarios that we introduce next, one would come to similar conclusions for a reduction of the effectiveness in spending on processes or candidates.Footnote 31
Election War
The setup so far adequately captures some empirical cases. But, it would not deal satisfactorily with the emerging problem of competition with powers that are not committed to democracy (Ambrosio Reference Ambrosio2008; Risse and Babayan Reference Risse and Babayan2015; von Soest Reference von Soest2015). Scholars have coined the term “black knights” for powers entering a conflict between an incumbent government and an outside actor in order to support the incumbent. When the conflict is an election, a black knight may alter the dynamics of the competition between government and opposition.
We next introduce a simultaneous move game, where two powers invest in elections. We call these scenarios “election wars” to emphasize the potentially conflictual nature of the interaction. The term also suggests that elections can be “proxy wars.” Much like during the Cold War, the United States and the Soviet Union would not combat each other directly, but used other arenas and players to fight indirectly. Elections can be thought of as a proxy conflict over influence. The United States could be considered to be (the liberal) power in the models that follow.
If both powers mutually support one side/party, or if the opposing side has a considerably smaller budget or smaller stake in the election, then the problem becomes a special case of the hegemony problem from the The Hegemon Case section.
We use the same formal specification for vote shares and bias as before, setting c = c − + c + and p = p − + p +. The optimization problem of the respective powers becomes
$$\begin{eqnarray*}
&&\max\limits_{c_+,p_+} \pi \Gamma _+ \left[ \chi + c_+ + c_- + \left(\sqrt{b}-(p_+ + p_-)\right)\right.\\
&&\left.\quad\times\,\left(\sqrt{b}-(c_+ + c_-)\right)\right] \\
&& -\, \Lambda _+\left(b-\sqrt{b}(p_+ + p_-)\right)-c_+^2-p_+^2, \\
&& \max\limits_{c_-,p_-} -\pi \Gamma _-\left[ \chi + c_+ + c_- + \left(\sqrt{b}-(p_+ + p_-)\right)\right.\\
&&\left.\quad\times\,\left(\sqrt{b}-(c_+ + c_-)\right) \right] \\
&& \quad- \Lambda _-\left(b-\sqrt{b}(p_+ + p_-)\right)-c_-^2-p_-^2.
\end{eqnarray*}$$
The Nash equilibrium of this simple two-player game is derived in Appendix Formal Solution of the Election War Case. Now investment c + of the power that likes the government whenever π > 0, is a response function to the choices of c − and p − by the power that likes the opposition. The same applies to investment in processes: the investment of the power that likes the government if π > 0 is denoted by p +, and it is a response function to the choices of c − and p − by the power that prefers the opposite of the political spectrum.
The Liberal Symmetric Election War
The most straightforward election war case simply adds another power with opposite political preferences that cares equally about liberalism and assigns the same geopolitical importance to the target country. We use Γ+ = 0.75, Λ+ = 0.5, Γ− = 0.75, Λ− = 0.5, and the rest of the parameters as in the election hegemon scenario.
The Nash equilibrium, derived in Appendix A.3, consists of a unique combination of c*+, c*−, p*+ and p*−, at which none of the powers has an incentive to unilaterally deviate to any alternative spending pattern. Below, we discuss informally its properties.
In a symmetric election war, powers care about liberalism and therefore have aligned interests in this regard. With respect to policies, however, their preferred platforms are on opposite sides of the political spectrum. One consistent change in all war scenarios relative to the hegemon case is that the entry of a second power improves the performance of the party the hegemon dislikes. That party now has an ally. We refer to this as the “levelling effect” of conflict.
While the effects of spending toward a certain candidate will benefit one of the powers at the expense of the other, the effects of spending on processes p are more subtle. The direct effect of a bias reduction on the vote share is comparable to the effect of spending on candidates, but at the same time spending on p has certain “public good” characteristics if both powers care about liberalism. Additionally, process spending interacts with spending on candidates, which would boost its effects whenever total net spending on candidates (c + + c −) is nonzero. Therefore, each power has the incentive to counteract spending by the other power.
Predictions. The result is a perfect standoff between the two international powers. In our baseline scenario, there is opposing investment in both candidates and processes, with c + = −c − and both p + > 0 and p − > 0 – where p + is decreasing in π and p − is increasing in π (cf. Figure 10 in Appendix The Liberal Symmetric Election War). The reasons for opposing investment in candidates are clear and have to do with opposing preferences over platforms. Investment in processes rises for one of the powers as it falls for the other because having one’s favorite candidate in opposition increases the incentive to invest in the rules, whereas having the favored candidate in government lessens that. There is positive net spending on p (p + + p − > 0), because both parties care about liberalism.
A change in polarization does not affect the overall sum of spending on candidates and processes by the two powers. Therefore, the election result does not depend on polarization and for most levels of polarization voters benefit from a lower election bias compared to the election hegemon.Footnote 32
Prior work suggests that when liberal states hold a preponderance of power in world affairs, this encourages democratization (Boix Reference Boix2011; Huntington Reference Huntington1991). This proposition rests on many causal arguments, one of which is international commitment to free elections. In the previous section, we showed that when power is commanded by a single democratic hegemon, its commitment to democracy depends on the stakes, polarization, and who is in power. However, when one liberal power is pitted against another, the result is always cleaner elections.Footnote 33 Thus, we clarify the logic of liberal preponderance that leads to democracy by showing that some conflicts among foreign powers may benefit elections.
The Asymmetric Election War
Next, we introduce two types of asymmetries, in the stakes and in commitment to liberalism. We also clarify how our propositions may be tested.
First, we consider the asymmetric election war case, in which a liberal outside power (+) competes against another power (−) with more at stake in the target country, i.e., a higher Γ. We vary this parameter to offer a sense of how this changes the results. At the same time, the second power is indifferent to, or even hostile towards, democracy. Recall that we call a power indifferent to democracy “aliberal” and a power hostile to democracy “illiberal.”
Predictions. Figure 6 illustrates the predictions.Footnote 34 For the case of a contest with a power indifferent to democracy (Λ− = 0), Figures 6a and 6b show opposing candidate investment, and opposing, but overall positive, investments in processes. Since one of the powers has more at stake in the target country, its total spending will always slightly exceed spending by the other power. Note that spending on p has no “public good”–characteristics from the perspective of the “−” power in this case. Additionally, spending by an aliberal power will be completely “opportunistic,” i.e., solely guided by the policy preferences of the power.
FIGURE 6. Equilibrium Choices in Election War Against a Higher-Stakes Power
In an election war between a liberal and an illiberal power (Λ− < 0), just as before, both investments in candidates and in processes are competing (cf. Figures 6c and 6d), but the overall bias might even increase compared to its ex ante level b through the intervention of the powers. For example, when the illiberal power likes the government in a polarized setting (the left-hand side of Figures 6e and 6f), it invests heavily against democracy and for its candidate. Because the stakes are higher for the illiberal power, its spending dominates and drives the outcome to the highest level of bias. It also leads to very good showing of the incumbent government.Footnote 35
Note that election wars continue to have a levelling effect, so that the difference between incumbent and opposition performance is less pronounced than it would be in the hegemon case.
To show how varying the stakes matters, we next consider a similar set of cases, except the power opposing the liberal one has lower stakes in the elections (Γ+ > Γ−). Figure 7 illustrates.Footnote 36 Figures 7a and 7b show opposing candidate investments, and opposing, but overall positive, process investments. Since the liberal power has more at stake in the target country, it will always spend slightly more than the opposing power.
FIGURE 7. Equilibrium Choices in Election War Against a Lower-Stakes Power
An aliberal opponent is opportunistic on democracy—sometimes spending to promote it, sometimes spending to erode it.
The picture changes for the case where the opponent is an illiberal power. Most of the time investments in candidates and processes are competing in opposite directions (cf. Figures 7c and 7d). Even though the liberal power is the stronger one, the overall bias might still increase from the intervention of the powers. Figures 7e and 7f show the implications for bias and party performance. The party liked by the liberal hegemon does better (Figure 7e), and bias is at its highest level when that party is in government (Figure 7f).
Case Studies
We recap some of the comparative statics we identify in election wars. Relative to the liberal hegemon case, the entry of an illiberal power leads to lower net investment in processes and more biased elections. The aliberal entry case is more nuanced. If the aliberal power likes the opposition, then it results in lower bias. In all the “war” cases, as the stakes for one power increase, the candidate favored by that power is doing better.
As the stakes for a power increase, there will be more investment in candidates by that power, which will only be partly counteracted by the other power. This holds in the same way for the liberal power, as well as for aliberal and illiberal powers. Investment in processes also follows the general pattern of the hegemon scenario: if the foreign power likes the opposition, there will always be cleaner elections; if the foreign power prefers the policy platform of the opposition, it will lead to lower levels of p. The implications from lower levels of p might vary across different scenarios. These implications include decreasing net positive spending on process improvements in a war against an aliberal power or further deterioration of democratic standards for the election war against an illiberal power.
Thus, we can help shed light on research on “black knights” (Risse and Babayan Reference Risse and Babayan2015), which leaves open the question of whether a liberal power may counteract the election manipulations of the (illiberal) black knight. An election war against an illiberal power makes it very costly for a liberal power to achieve its desired election outcomes. The impact also depends on the (relative) stakes for the two powers.
Consider Ukraine’s 1991, 1994, and 2004 presidential elections as illustrations of some of the “election war” scenarios. While domestic conditions are important, so are the interests of outsiders. Ukraine is an important country for both the United States and Russia. The 1991 election concluded with the election of Leonid Kravchuk, in a case where the United States preferred the opposition (more nationalist) candidate over Kravchuk.Footnote 37 Polarization was relatively low, since both candidates promised reforms and independence—the key issue at stake. During this period, the Soviet Union was facing significant financial difficulties and it was not necessarily opposed to the promotion of democracy. We can think of this case as an illiberal-aliberal war, or, due to the Soviet financial problems, as a case that fits the stylized description of a liberal (U.S.) hegemonic intervention.Footnote 38 Either way, based on the middle portion of the graph in Figure 7f, we would predict a relatively clean contest. While the election was not problem free, election observers were satisfied with its integrity.
In the 1994 elections, Leonid Kuchma, the pro-Russian opposition candidate for President of Ukraine, defeated the incumbent Kravchuk in an election that was biased but again substantially free of significant fraud.Footnote 39 In this case, both the United States and Russia invested heavily in opposing campaigns: the United States preferred the incumbent (Kuchma) to win, whereas Russia (still relatively liberal and so, not opposed to democracy) backed the opposition.Footnote 40 This result is consistent with the right-hand side (positive π) of the election liberal-aliberal bias prediction in Figure 6f. Rising stakes for the aliberal power and both powers contributing some investment for cleaner processes puts the predictions of bias low, similar to the 1991 case.
In the 2004 elections, pro-Western opposition candidate Yuschenko faced significant vote rigging. Only after mass protests that followed the second round of voting—what became known as the Orange Revolution—did he manage to win.Footnote 41 The United States pressed for democratic elections, whereas Russia helped the incumbent manipulate the electoral process. This was a case where Russia had shifted to a less liberal position in its preferences (democracy deteriorated domestically), and backed the incumbent to win. Russia had redefined its security interests in a manner that made control of Ukraine a paramount strategic objective. For the purposes of our model, bias is at the highest possible point in this context. The observed outcome—a greater degree of fraud—is consistent with the predictions from the model. This is illustrated in the left-hand side (π < 0) of Figure 6f.Footnote 42
Superpower Utility
Finally, we note that investing in the elections of others is not necessarily utility enhancing for the outside powers. In election wars against powers that do not value—or even oppose—democracy, a liberal hegemon’s utility is generally low. In fact, both intervening states may be better off jointly committing not to intervene than expending resources against each other. Thus, even where an election goes the way a superpower prefers, the victory of an election race may be of dubious value. Figure 8 illustrates this.
FIGURE 8. Utility of the Foreign Liberal Power
DISCUSSION
The comparative statics, illustrated across different scenarios and parameter values, provide testable propositions. We can use the geopolitical importance of a country, the level of domestic polarization, and the strategic setting of one or more powers intervening, together with their commitment to liberalism, to predict incumbent win and election bias.
Testing systematically the insights of the model in elections is a matter of identifying appropriate data. Such data should include a measure of policy positions, especially ideological proximity to important international powers, and differences between the government and opposition platforms. Unfortunately, available data are either simply not at this level, or are noisy empirical approximations.Footnote 43
Illustration
We construct a small dataset that tracks more closely our key variable polarization. The National Elections Across Democracy and Autocracy (NELDA) data have a number of election-level variables for more than 3300 election events (Hyde and Marinov Reference Hyde and Marinov2012). As a preliminary evaluation of our theory, we selected 63 election cases from NELDA and we coded whether the government and main opposition party were divided in their position on cooperation with the United States, as well as whether another power was active in the election.
We code the variable polarization in analogy to our model parameter π: polarization is 1 if the United States prefers the incumbent, − 1 if the United States prefers the opposition, 0 otherwise. Conditioning variable war_usa indicates that the United States faces an opponent, i.e., an election war scenario.Footnote 44 For the model’s two outcome dimensions, incumbent vote gain and bias, we use NELDA variables nelda27 Footnote 45 and nelda11,Footnote 46 respectively.
Table 1 shows the mean, standard deviation and number of observations conditional on polarization and whether an election “war” or “hegemony” case (hegemony here means a case where the United States does not face competitors). Figure 9 presents the tabular information in graphical form.
FIGURE 9. NELDA Data on Outcomes
TABLE 1. NELDA Data on Outcomes
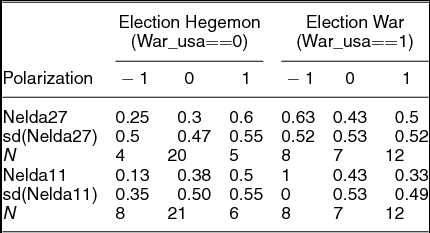
Our liberal hegemon predictions (Figure 2) lead us to expect better performance of the candidate(s) aligned with the United States and worse performance for the candidates that oppose the United States. We also expect election bias to follow the same patterns. We see in Figure 9 that, when the incumbent is friendly to the United States, i.e., the variable Polarization is coded as 1, the incumbent does better in elections. The boost is nontrivial. We also see that this is correlated with bias (in favor of the incumbent).
For election war cases we would expect a different dynamic (Figures 6 and 7). Whenever the United States is aligned with the government, the rival power is aligned with the opposition. We would expect a decrease in the effect of polarization on the vote shares (levelling effect). Figure 9a shows that “wars” level the playing field and lessen the importance of being an ally to the United States (relative to the hegemony case).
From the election war cases, we see that the fraction of biased elections decreases for non-negative values of polarization π ⩾ 0 (Figure 9b). This would be consistent with a conflict between a liberal and an aliberal power, where the stakes are higher for the opposing, aliberal power—possibly due to regional interests. If the aliberal power is aligned with the opposition (and there is a pro-U.S. incumbent; i.e., π > 0) there are cleaner elections because democracy promotion is in the interest of both powers. While if the pro-U.S. party is in opposition, the United States is the sole power with an interest in democracy. Our theory, thus, would predict spending by the aliberal power on the deterioration of democracy for π < 0.
Our predictions are more fine grained than the cases available for empirical examination. Future data collection can enable us to test more rigorously the model’s predictions.Footnote 47 The empirical exercise suggests that external alignments are consequential for who wins elections, and how they win them. Furthermore, the effects are clearly discernible simply in the raw data.
The Effect of Democratic International Organizations
International organizations, dominated by democracies, have different ways of cajoling elites into committing to reforms and sticking with them (Pevehouse Reference Pevehouse2002). Unlike states, which feel compelled to prioritize geopolitical agendas over democracy promotion (Reiter Reference Reiter2001), international organizations can delegate the enforcement of democratic norms to specialized bureaucracies and deploy impartial election observers (Hyde Reference Hyde2011).
If we add to our baseline scenario a strategic outside actor that is only committed to liberalism, we can easily incorporate international organizations into our model. Since the policy outcome (which party wins) does not matter to the international organization, it will spend a constant amount p on bias reduction, regardless of political divisions. As we show in the Online Appendix The Effect of (Democratic) International Organizations, international organizations, committed to democracy, offset partisan-driven, democracy-eroding interventions in any strategic context and are always good for democracy.
Regime Overthrow
One might think of the option to decide—ex ante—to influence a democratic regime via contributions towards candidates and processes or whether to simply attempt to overthrow the regime. In the case of Greece, for example, U.S. interventions helped nudge the political right to victory for two decades after WWII. After the left won a decisive victory in 1965, the army intervened with tacit U.S. backing (Couloumbis and Iatrides Reference Couloumbis and Iatrides1980). One easy specification for this effect would be to allow overthrow at a fixed cost r and an additional cost Λ for those international powers that care about democracy. We look at this case in the Online Appendix Regime Overthrow. We show that a high degree of candidate polarization may induce the interveners to abandon interventions in elections in order to pursue supplanting democracy. The latter is more likely for an illiberal power.
Endogenous Choice of Policy Positions
Realistically, parties may change their policy positions in order to attract outside funding. Indeed, this is a possible explanation of what occurred in post-WWII Italy. National Security Advisor McGeorge Bundy complained that the ritual of Christian Democrats petitioning for money to stave off a Communist takeover—and the United States obliging—was America’s “annual shame” (Mistry Reference Mistry2006, p. 319). Democrazia Christiana adopted consistently and rigorously pro-American stances, even volunteering that Italy should join NATO at an early stage. The Online Appendix Endogenous Choice of Policy Positions extends our model to allow for candidates choosing their platforms endogenously. This adds a first stage in which both the government and the opposition simultaneously determine their platforms. We present a simplified version of an exercise similar to Grossman and Helpman (Reference Grossman and Helpman1996). We show that positions shift to a larger extent and polarization grows more in the hegemon case. When both sides have an ally, there is a more level playing field and changing positions is less rewarding for attracting support that generates additional votes. The gap in the policy positions of the two parties shrinks when the party that is farther away from the outsider with higher stakes in the election finds it easier to compromise its position and adopt a more proforeign stance.
CONCLUSION
The conceptual distinctions we develop in this paper should help further debates on democracy promotion. Observers and scholars worry that the partisan bias in U.S. democracy assistance undermines the effort’s effectiveness.Footnote 48 We outline a distinction between candidate interventions (i.e., the “who” of elections) and process interventions (i.e., the “how” of elections). We argue that investments in processes and parties are mutually dependent. The value of additional investment in candidates will depend on the rules of the game. Policy polarization between candidates and the geopolitical importance to the intervener determine the balance of candidate and process investments in each contest.
We contribute to work on diffusion of democracy (Gleditsch and Ward Reference Gleditsch and Ward2006; Weyland Reference Weyland2009). Scholars have asked how international forces change the conduct of elections (Flores and Nooruddin Reference Flores and Nooruddin2016; Rozenas Reference Rozenas2015). We offer a more precise understanding of how the distribution of power affects electoral integrity. While interest in building institutions and in helping allies sometimes clash, we show that this is not necessarily the case. Our work on what we call election wars—conflictual investments by outsiders in different candidates—shows that outsiders sometimes bid for a paltry return and may even be better off if they could jointly commit not to intervene.
Our theoretical approach suggests avenues for further research. Empirically, we need information on how foreign actors value the opposition, not only the government. The gap in preferences for a government or opposition win has bearing on election interventions, and, via this channel, on democracy itself. Who holds power, how close relations are between states, and what is the state of democracy domestically all depend on the strategic incentives of outside powers.
Theoretically, our model can be extended to cover the different manners in which foreigners “make votes count” (Cox Reference Cox1997). One could allow for more than one round to see the effects of the differing persistence of investment in candidates and processes—incorporating a quintessential feature of democratic elections: that they repeat over time. The possibility of corruption is another natural avenue for further research. Finally, our model can be applied to domestic elections, where we can have, in a federal system, powerful lobbies square off against each other in investing in better rules or in their candidates. These and other areas of study can benefit from the theory we propose.
APPENDIX
Solution of the Election Hegemon Problem
We can solve the first of the FOCs for c and plug into the second FOC:
$$\begin{equation*}
p^* = \frac{\sqrt{b}\left(\pi \Gamma -\Lambda \right)+\frac{\Gamma ^2\pi ^2}{2}\left(\sqrt{b}-1\right)}{\frac{\pi ^2 \Gamma ^2}{2}-2},
\end{equation*}$$
and for c* we get
$$\begin{eqnarray*}
c^* &=&\frac{\pi \Gamma }{2} \left(p^* - \sqrt{b} + 1\right)\\
& = &\frac{\pi \Gamma }{2} \left(\frac{\sqrt{b}\left(\pi \Gamma -\Lambda \right)+\frac{\Gamma ^2\pi ^2}{2}\left(\sqrt{b}-1\right)}{\frac{\pi ^2 \Gamma ^2}{2}-2}-\sqrt{b}+1\right).
\end{eqnarray*}$$
From our FOCs it also follows that the Hessian is
$$\begin{equation*}
H = \left( \arraycolsep5pt\begin{array}{cc}-2 & \pi \Gamma \\
\pi \Gamma & -2 \end{array} \right).
\end{equation*}$$
The second order sufficient condition for a critical point to be a maximum is that the Hessian be negative definite at the critical point. Therefore, we need the principal minors |H 11| = −2 < 0 and
$$\begin{equation*}
\left| \arraycolsep5pt\begin{array}{cc}H_{11} & H_{12} \\
H_{21} & H_{22} \end{array} \right| = 4-\pi ^2\Gamma ^2 > 0.
\end{equation*}$$
This holds if |πΓ| < 2.
Formal Solution of the Constrained Optimization Problem
$$\begin{equation*}
\arraycolsep5pt\begin{array}{cl}\max _{c,p} & \pi \Gamma \left(\chi + (1-\sqrt{b}+p)c + b - \sqrt{b}p\right)\\
&\quad - \Lambda \left(b-\sqrt{b}p\right)-c^2-p^2 \\
& s.t. \quad c^2+p^2 \le y. \end{array}
\end{equation*}$$
We have
$$\begin{eqnarray*}
\mathcal {L}_\lambda (c,p) &=& \pi \Gamma \left(\chi + (1-\sqrt{b}+p)c + b - \sqrt{b}p\right) \\
&&-\, \Lambda \left(b-\sqrt{b}p\right)-c^2-p^2-\lambda (c^2+p^2-y).
\end{eqnarray*}$$
This yields the following first order necessary conditions for a maximum:
$$\begin{equation*}
\arraycolsep5pt\begin{array}{rcll}\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c}\hspace{0.0pt}}}} & = & \pi \Gamma \left( 1 -\sqrt{b}+p \right)-2c -2\lambda c & {\buildrel!\over=}0, \\[10pt]
\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p}\hspace{0.0pt}}}} & = & \pi \Gamma \left( c-\sqrt{b} \right)+\Lambda \sqrt{b}-2p - 2 \lambda p & {\buildrel!\over=}0,\\
& & c^2 + p^2 - y & \le 0,\\
& & \lambda & \ge 0,\\
& & \lambda (c^2+p^2-y) & {\buildrel!\over=}0. \end{array}
\end{equation*}$$
If λ = 0 then the problem is the same as in the unconstrained optimization problem. If λ ⩾ 0 then we can use the binding budget constraint to solve for c:
$$\begin{equation*}
c=\pm \sqrt{y-p^2},
\end{equation*}$$
and from the first two FOCs we get
$$\begin{equation*}
\frac{\pi \Gamma }{2c} \left(1-\sqrt{b}+p\right) - 1 = \lambda
\end{equation*}$$
and
$$\begin{equation*}
\frac{\pi \Gamma }{2p} \left(c-\sqrt{b}\right) + \frac{\Lambda \sqrt{b}}{2p}- 1 = \lambda .
\end{equation*}$$
Setting these equal leads to
$$\begin{equation*}
p\left(1-\sqrt{b}+p\right) = c \left(c-\sqrt{b}\right) + c \frac{\Lambda \sqrt{b}}{\pi \Gamma }.
\end{equation*}$$
We plug in the two possible solutions for c (i.e.,
$\pm \sqrt{}$
) we obtained from the binding budget constraint and solve both,
$$\begin{equation*}
p_+^*\left(1-\sqrt{b}+p_+^*\right) = \sqrt{y-{p_+^*}^2} \left(\sqrt{y-{p_+^*}^2}-\sqrt{b}+ \frac{\Lambda \sqrt{b}}{\pi \Gamma } \right),
\end{equation*}$$
for p*+ such that
$c_+^*=\sqrt{y-{p_+^*}^2}$
and
$\lambda _+^*=\frac{\pi \Gamma }{2c_+^*} \left(1-\sqrt{b}+p_+^*\right) - 1$
and
$$\begin{eqnarray*}
&&p_-^*\left(1-\sqrt{b}+ p_-^*\right)\\
&&\quad = -\sqrt{y-{p_-^*}^2} \left(-\sqrt{y-{p_-^*}^2}-\sqrt{b}+ \frac{\Lambda \sqrt{b}}{\pi \Gamma } \right)
\end{eqnarray*}$$
for p*− such that
$c_-^*=-\sqrt{y-{p_-^*}^2}$
and
$\lambda _-^*=\frac{\pi \Gamma }{2c_-^*} (1-\sqrt{b}+p_-^*) - 1$
. The utility maximum for a binding budget constraint is at the solution to these FOCs for which λ ⩾ 0 holds unless the solution is a corner solution. We omit the second order constraints we could derive from a bordered Hessian here. If there is a solution with λ = 0 and c*2 + p*2 ⩽ y, this solution points to the optimal composition of spending.
Formal Solution of the Election War Case
There are two ways to approach this problem in general: One is to solve a system of four linear equations in four variables, namely c +, c −, p +, p −,
$$\begin{equation*}
\arraycolsep5pt\begin{array}{rcll}\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}} & = & \pi \Gamma _+ \left(p_- +p_+ - \sqrt{b} + 1\right) - 2 c_+ & {\buildrel!\over=}0, \\
\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}} & = & \Lambda _+ \sqrt{b} - 2p_+ + \pi \Gamma _+ \left(c_-+c_+-\sqrt{b}\right) & {\buildrel!\over=}0, \\
\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_-}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_-}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_-}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_-}\hspace{0.0pt}}}} & = & -\pi \Gamma _- \left(p_- +p_+ - \sqrt{b} + 1\right) - 2 c_- & {\buildrel!\over=}0, \\
\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_-}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_-}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_-}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_-}\hspace{0.0pt}}}} & = & \Lambda _- \sqrt{b} - 2p_- - \pi \Gamma _- \left(c_-+c_+-\sqrt{b}\right) & {\buildrel!\over=}0. \\
\end{array}
\end{equation*}$$
This is equivalent to the more intuitive way of plugging in the best response of the “−” power into the FOCs of the “+” power and thereby deriving a best response of the one power to the best response of the other power. The necessary steps will be shown in the following:
First we derive the best responses of the “−” player,
{\fontsize{7}{9}\selectfont{$$\begin{eqnarray*}
&&c_-^*(c_+,p_+)\\
&&\quad = \frac{\pi \, \Gamma _-\, \left(2\, p_+ + \Lambda _-\, \sqrt{b} - 2\, \sqrt{b} - \Gamma _-\, c_+\, \pi + \Gamma _-\, \sqrt{b}\, \pi + 2\right)}{ {\pi }^2\Gamma _-^2\, - 4},\\
&& p_-^*(c_+,p_+)\\
&&\quad = - \frac{2\, \Lambda _-\, \sqrt{b} + \Gamma _-^2\, {\pi }^2 + \Gamma _-^2\, {\pi }^2\, p_+ - 2\, \Gamma _-\, c_+\, \pi - {\Gamma _-}^2\, \sqrt{b}\, {\pi }^2 + 2\, \Gamma _-\, \sqrt{b}\, \pi }{\Gamma _-^2\, {\pi }^2 - 4}.
\end{eqnarray*}$$}}
Subsequently we plug in
{\fontsize{6}{8}\selectfont{$$\begin{eqnarray*}
&&\mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}c_+}\hspace{0.0pt}}}} \\
&&\quad = \pi \Gamma _+ \left(- \frac{2\, \Lambda _-\, \sqrt{b} + \Gamma _-^2\, {\pi }^2 + \Gamma _-^2\, {\pi }^2\, p_+ - 2\, \Gamma _-\, c_+\, \pi - {\Gamma _-}^2\, \sqrt{b}\, {\pi }^2 + 2\, \Gamma _-\, \sqrt{b}\, \pi }{\Gamma _-^2\, {\pi }^2 - 4} \right.\\
&&\left.\qquad+\,p_+ - \sqrt{b} + 1\right) - 2 c_+ \, {\buildrel!\over=}\, 0, \\
&& \mathchoice{\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}{\displaystyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}}{\scriptstyle {\frac{\partial \hspace{0.0pt}\cdot }{{\partial \hspace{0.0pt}p_+}\hspace{0.0pt}}}} \\
&&\quad = \Lambda _+ \sqrt{b} - 2p_+ + \pi \Gamma _+\\
&&\quad\times\, \left(\frac{\pi \, \Gamma _-\, \left(2\, p_+ + \Lambda _-\, \sqrt{b} - 2\, \sqrt{b} - \Gamma _-\, c_+\, \pi + \Gamma _-\, \sqrt{b}\, \pi + 2\right)}{ {\pi }^2\Gamma _-^2\, - 4}+c_+-\sqrt{b}\right) \, {\buildrel!\over=}\,0.
\end{eqnarray*}$$}}
Both solution methods lead to
{\fontsize{6}{8}\selectfont{$$\begin{eqnarray*}
c_+^* & = & - \frac{2 \pi \Gamma _+ - {\Gamma _+}^2 {\pi }^2 \sqrt{b} - 2 \pi \Gamma _+ \sqrt{b} + \pi \Gamma _+ \Lambda _+ \sqrt{b} + \pi \Gamma _+ \Lambda _- \sqrt{b} + \Gamma _+ \Gamma _- {\pi }^2 \sqrt{b}}{{\pi }^2 {\Gamma _+}^2 - {\pi }^2 \Gamma _+ \Gamma _- 2 + {\pi }^2 {\Gamma _-}^2 - 4}, \\
p_+^* & = & - \frac{\begin{array}{l}
\left(4 \Lambda _+ \sqrt{b} + 2 {\Gamma _+}^2 {\pi }^2 - 2 {\Gamma _+}^2 {\pi }^2 \sqrt{b} - 2 \Gamma _+ \Gamma _- {\pi }^2 - 4 \pi \Gamma _+ \sqrt{b} + 2 \Gamma _+ \Gamma _- {\pi }^2 \sqrt{b} \right.\\
\left.\quad+\, {\Gamma _+}^2 \Lambda _- {\pi }^2 \sqrt{b} - {\Gamma _-}^2 \Lambda _+ {\pi }^2 \sqrt{b} + \Gamma _+ \Gamma _- \Lambda _+ {\pi }^2 \sqrt{b} - \Gamma _+ \Gamma _- \Lambda _- {\pi }^2 \sqrt{b}\right)
\end{array}}{2 \left({\pi }^2 {\Gamma _+}^2 - {\pi }^2 \Gamma _+ \Gamma _- 2 + {\pi }^2 {\Gamma _-}^2 - 4\right)}, \\
c_-^* & = & \frac{2 \pi \Gamma _- + {\Gamma _-}^2 {\pi }^2 \sqrt{b} - 2 \pi \Gamma _- \sqrt{b} + \pi \Gamma _- \Lambda _+ \sqrt{b} + \pi \Gamma _- \Lambda _- \sqrt{b} - \Gamma _+ \Gamma _- {\pi }^2 \sqrt{b}}{{\pi }^2 {\Gamma _+}^2 - {\pi }^2 \Gamma _+ \Gamma _- 2 + {\pi }^2 {\Gamma _-}^2 - 4}, \\
p_-^* & = & - \frac{\begin{array}{l}
\left(4 \Lambda _- \sqrt{b} + 2 {\Gamma _-}^2 {\pi }^2 - 2 {\Gamma _-}^2 {\pi }^2 \sqrt{b} - 2 \Gamma _+ \Gamma _- {\pi }^2 + 4 \pi \Gamma _- \sqrt{b} + 2 \Gamma _+ \Gamma _- {\pi }^2 \sqrt{b}\right.\\
\left.\quad -\, {\Gamma _+}^2 \Lambda _- {\pi }^2 \sqrt{b} + {\Gamma _-}^2 \Lambda _+ {\pi }^2 \sqrt{b} - \Gamma _+ \Gamma _- \Lambda _+ {\pi }^2 \sqrt{b} + \Gamma _+ \Gamma _- \Lambda _- {\pi }^2 \sqrt{b}\right)
\end{array}}{2 \left({\pi }^2 {\Gamma _+}^2 - {\pi }^2 \Gamma _+ \Gamma _- 2 + {\pi }^2 {\Gamma _-}^2 - 4\right)}.
\end{eqnarray*}$$}}
The Liberal Symmetric Election War
The Liberal Symmetric Election War adds another power with opposite political preferences that cares equally about liberalism and assigns the same geopolitical importance to the target country (see Fig. 10).Footnote 49
FIGURE 10. Equilibrium Choices and Outcomes in Liberal Symmetric Election War
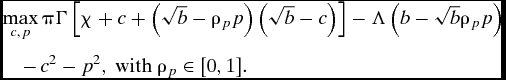
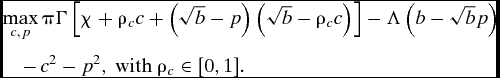
Comments
No Comments have been published for this article.