Introduction
The aggregate rheology of sea ice depends ultimately on the geometry and the failure strength of the interactions between individual ice floes. Attempts to estimate the aggregate rheology have either made use of treatments of the sea-ice ridging process (Reference CoonCoon, 1974; Reference RothrockRothrock, 1975) or made use of deformation-induced collision theory for rapid granular flow (Reference Shen, Hibler, III, and Leppäranta.Shen and others, 1987; Reference BratchieBratchie, 1984). Both of these methods have their limitations, In the ridging approach, whereas the ice strength may be deduced from the nature of the ridging process, assumptions must be made to define the shape of the yield curve and the plastic flow rule. In the collision theory, the failure stresses arise from consistent calculations, but the theory cannot treat a very dense collection of floes, where the contacts between floes are relatively continuous.
As a first step toward modeling a very compact system of ice floes, a series of numerical experiments is performed using an explicit particle simulation. In the simulation, a large number of random-diameter interacting disks represent the floes. The idea behind the experiments is to determine the large-scale aggregate failure stresses as a function of the ratio of the strain-rate invariants for a dense system, in which the interactions between floes in contact are viscous-plastic.
The Particle Simulation
A particle simulation is a computer program which models the Newtonian dynamics of a large system of discrete particles which are confined to a domain or control volume. The simulation stores the instantaneous position and velocity of each particle. The particles which overlap at any given moment are considered to be in contact. In the present model, the forces between contacting pairs of disks are related to the relative velocity between the disks at their point of contact (including rotational components).
The two-dimensional control area (CA) used in these experiments is rectangular and periodic. It contains N disk-shaped particles of non-uniform diameter. As a disk crosses a boundary of the CA, it simultaneously re-enters the CA through the opposite boundary. A disk near one boundary may interact with disks near the opposite boundary. In order to model the inter-particle contact forces, a list of neighboring pairs of disks is compiled periodically. The strategy used to compile the list begins by overlaying the CA with a square grid. Each cell of the grid is small enough that, at most, one disk center may lie in a cell at a time. An array is dimensioned to correspond with the grid and the index of each disk is assigned to the array element corresponding to the cell in which its center lies. In addition, two inverse address arrays are defined. One holds the i location of a disk and the other j location, where i denotes a column and j a row in the grid. These arrays enable the program to find the disk located at (i,j) in the CA and the address of a given disk. With this information, it is a straightfoward matter to find the close neighbors of each of the N disks. The pairs of disks which are discovered less than some arbitrarily small distance apart are placed in an array of near neighbors, which is refreshed periodically. At each time step, each pair of disks in the array of near neighbors is checked for contact.
Deformation of the CA is accomplished by distorting
space in a manner analogous (at least in the case of isotropic compression) to the deflation of a balloon with the disks constrained to its surface. This type of simulation technique was developed by Reference Cundall and StrackCundall and Strack (1979) to create a mean deformation field in a material, without the use of boundaries which create inhomogeneities in the material. The equations of motion which define disk motions in the deformed space are standard difference equations, with an additional term which models the uniform deformation of the CA.
At each time step, ΔΔ, the change in the position, x, of each disk has a component due to the velocity of the disk, u, and to the simultaneous deformation of space

In Equation (1) the subscripts i and j denote directions in Cartesian space, the superscript n denotes the current time step, and


where F is the resultant of the contact forces on the disk and m is the mass of the disk. The relative velocity between two disks, designated disk 1 and disk 2, is a function of their velocities and the strain rate of space

Contact between a pair of disks exists when the disks overlap. If a pair of disks is found to overlap, a local orthogonal coordinate system (n,t) is established with its origin at the point of contact. The normal axis, n, is perpendicular and the tangential axis, t, is tangential to the surface of the disks. The normal component of the inter-particle force is linear viscous

where kv is the viscous damping coefficient. The magnitude of the viscous normal force has a plastic limit, P* such that
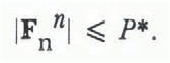
Tensile forces are not allowed. The tangential, frictional component of the inter-particle force, which opposes the relative velocity at the contact point, is

where ks is a spring constant and μ is the coefficient of friction. The magnitude of the frictional force also has a limit
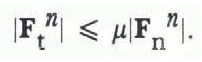
A sample experimental configuration is shown in Figure 1. Each short bar in the figure, centered at a point of contact, represents the instantaneous value of the contact force between that pair of disks. The width of the bar corresponds to the magnitude of the force and its

Fig. 1. The periodic control area with contact force vectors.
orientation shows the relative magnitudes of the normal and tangential components. This method of illustrating the lines of force is taken from Reference Cundall and StrackCundall and Strack (1979). The instantaneous value of the stress tensor in the CA is computed using the equation given by Reference Cundall, Satake and JenkinsCundall (1988)

where A is the area of the CA, ΣP is the summation over all particles, r P is the radius of particle P, Σc is the summation over all contacts on particle p, and ni is the unit normal and F j the force vector at contact c. The instantaneous value of the stress tensor in the CA is averaged over successive time steps in a given interval to determine the average stress tensor.
Description of the Experiment
Experimental samples or collections of disks were generated by loosely filling the CA with disks. The diameter d of each disk was randomly chosen according to the formula
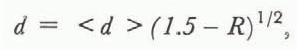
where <d> is the average diameter and R is a random number between 0 and 1. The disks are placed loosely in the CA, given a random velocity, and the CA is slowly and isotropically contracted. A linear elastic normal contact force is used in this phase of sample preparation. As the sample reaches maximum concentration, the stresses rise rapidly. At maximum concentration, the convergence is stopped, the elastic normal force is turned off, the viscous-plastic force (Equation 4) is turned on, and the system is allowed to relax. Three different samples were prepared in this manner for each coefficient of friction.
A series of experiments, with a given value of μ and kν , were performed on each sample, in which the convergent (ė > 0) principal strain ratė1 was held constant while ė2
was varied from isotropic convergence (ė2=ė1) through pure shear (ė2=ė1). The roles of the principal strain rates were then exchanged and the experiments were repeated. All of the results obtained with a given ratio of principal strain rates were averaged to eliminate bias in the initial samples. Experiments with strain rates between isotropic convergence and pure shear create no net divergence and are essentially deformation independent because the network of contacts among the disks remains constant. The results of these experiments define an equilibrium yield curve, which is incomplete, because it does not specify the stress state for all possible strain rates. In order to close the yield curve, additional experiments with strain rates which create net divergence were performed. With net divergence, the results are deformation dependent because of the increasing void area in the material and the accompanying reduction in the number of contacts between disks. The complete yield curve is valid for small incremental deformations from a very dense initial state.
Discussion of the Results
Experiments were performed to assess the effects of different coefficients of friction and viscous damping on the shape of the yield curve in principal-stress space. The values of the following parameters were held constant throughout the experiments:
<d>0.05 m,
P*0.00625 N,
ė(constant) 0.02 s−1 (convergence positive),
ė(variable) 0.02, 0.01, 0.005, 0, −0.01, −0.02 s−1
k s 2.5 × 105 Ν m−1,
ρ(disk density) 1.0 kg m−3.
The values of the coefficients of friction and viscous damping which were used in the experiments are
μ0.1, 0.5, 1.0,
kv 25, 100, 2000Nsm−1.
The time step used in the experiments, which is derived from the equation for damped linear oscillation, is given by

The duration of experiments with k = 25 and 100 Ν s m −1 was 0.1 s, with stress averages calculated over sub-intervals of 0.02 s. The duration of experiments with kv = 2000 Ν s m−1 was 0.03 s, with stress averages calculated over sub-intervals of 0.002 s. Each experiment at kv =2000 required 5 h on an Alliant FX-40. In the figures, positive values of stress and strain denote compression and convergence, respectively. The dimensions of the plotted stresses are force (in units of P*) per unit area.
Figure 2 shows the results of experiments with different values of the coefficient of friction, μ. The strain-rate vectors associated with the principal stresses for μ = 1.0 are shown with their tails at the data points. The first points on the curves for μ = 0.1 and μ = 0.5 have the same values of the principal strain rates as the first point on the μ = 1.0 curve, and so on. As the strain-rate vectors are not perpendicular to the yield curves, the results violate the normal flow rule.

Fig. 2. Yield curves in principal-stress space for different values of the friction coefficient μ(kv = 100 Ν s m−1).
Whereas the shapes of the yield curves for the three values of μ are similar, the size, especially the breadth, increases with friction. The breadth of the yield curve (perpendicular to the axis of symmetry) is a function of the deviatoric stress. The components of the deviatoric principal stress, σ 1′ due to the normal and tangential components of the contact force, are shown in Table 1. The values correspond to the state of pure shear (the points nearest the origin on the yield curves in Figure 2). It is interesting to note that the normal component, as well as the tangential component, increases with friction.
Dimensional analysis yields the non-dimensional parameter,
Table 1. Normal, tangential and total deviatoric stresses in pure shear (ė1 = -ė2 = 0.02). Numbers are given in units of P*.


Fig. 3. Changes in the yield curves caused by increasing values of the viscous damping coifficient kv (μ = 0.5).
Experiments With Net Divergence
In a granular material, experiments with strain rates which create net divergence in the system are deformation dependent because of the increasing void area in the material and the accompanying reduction in the number of contacts between disks. In such deformation states, there is no equilibrium yield curve. However, experiments were performed with varying amounts of net divergence to obtain closed yield curves valid for small increments of deformation. The strain rates used in these experiments (in addition to those listed above) were
ė (constant) 0.02 s−1 (convergence positive),
ė (variable) −0.03, −0.04, −0.05, −0.076, −0.10 s−1.

Fig. 4. A complete deformation-dependent yield curve for small incremental deformation (μ = 0.5, kv = 2000 Nsm−1).
The viscous damping coefficient kv = 2000 Ν s m−1 and the duration of the experiments was 0.03 s with stress averages calculated in sub-intervals of 0.002 s. The results are presented in Figure 4. The three curves plotted in the figure show the yield curve at intervals of 0.01 s from the start of the experiment. (Note: for the first and third intervals only half of the yield curve is plotted.) The differences between stresses at given strain rates measured at the three times vary qualitatively with the amount of net divergence in the system. The stresses associated with strain rates approaching uniaxial divergence (the points nearest the origin) show rapid initial convergence toward the zero stress state where all three curves appear to be headed.
A final series of experiments was performed to test the effects of the size of the periodic CA on the results. In these experiments, the area of the CA and the number of disks were doubled, whereas all other parameters remained constant. The results were within the range of variation of the experiments performed in the smaller CA.
Conclusions
The numerical experiments described in this work provide the first estimate of the shape of the yield curve for a granular viscous-plastic material based on experimental data. Qualitatively, the shape of the yield curves described by the experiments lies somewhere between the tear drop and the lenticular yield curves (suggested by Reference RothrockRothrock (1975)) and is remarkably close to the 2:1 aspect ratio ellipse used by Reference Hibler,III.Hibler (1979).
The effects of the coefficients of friction and viscous damping on the shape of the yield curves were discussed. Increasing values of the friction coefficient increase the breadth of the yield curve (Fig. 2). This increase in
breadth, which is equivalent to an increase in the shear strength of the material, is the result of an increase in the parts of the deviatoric stress due to both the normal and tangential components of the inter-particle contact force. Increases in the viscous damping coefficient affect the shape of the yield curve (Fig. 3), probably by increasing the fraction of failing contacts, that is, the contacts with normal forces at the plastic limit. It was also observed that the strain-rate vectors associated with points on the yield curve in principal-stress space are not exactly perpendicular to the yield curves, violating the normal flow rule.
In granular systems, combinations of principal strain rates which produce net divergence weaken the material by increasing the open area and reducing the number of contacts between disks. Weakening of the material with increased divergence is manifest in the progressive reduction of the principal stresses for a given ratio of principal strain rates. In these deformation states there is no equilibrium yield surface. In the experiments with net divergence reported here, for small incremental deformation from an initially dense state, the yield curves (Fig. 4) appear to terminate at the origin in principal-stress space. This result is significant because, for the formation of an arch at a point where flow is constricted, a material must be capable of supporting a uniaxial-stress state. The yield curve for such a material would terminate on (or cross) the principal-stress axes. The fact that the yield curves terminate at the origin without crossing the stress axes suggests that the disk-shaped granular material used in the experiments is not capable of forming arches.
Acknowledgement
We would like to thank the Office of Naval Research for their long-term support through the University Research Initiative, contract number N00014-86-K-069.






