Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-21T16:06:20.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Collocation methods for two dimensional weakly singular integral equations

Published online by Cambridge University Press:  17 February 2009

Ivan G. Graham
Ivan G. Graham
Affiliation:
School of Mathematics, University of New South Wales, Kensington, NSW 2033
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

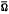Given a Fredhoim integral equation of the second kind, which is defined over a certain region ⊆ R2, we define 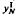and 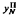, two different numerical approximations to its solution, using the collocation and iterated collocation methods respectively. We describe without proof some known results concerning the general convergence properties of 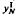and 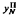when the kernel and solution of the integral equation are smooth. Then, we prove rigorously order of convergence estimates for 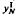and 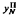which are applicable in the practically siginificant case when 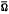is a rectangle, and the kernel of the integral equation is weakly singular. These estimates are illustrated by the numerical solution of a two dimensional weakly singular equation which arises in electrical engineering.

Type
Research Article
Information
The ANZIAM Journal , Volume 22 , Issue 4 , April 1981 , pp. 456 - 473
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Chandler, G. A., “Product integration methods for weakly singular second kind integral equations”, submitted for publication.Google Scholar
[2]Dewar, F. A., Solution of Fredholm integral equations by the Galerkin and iterated Galerkin methods (M. Sc. Thesis, University of New South Wales, 1980).Google Scholar
[3]Graham, I. G. and Sloan, I. H., “On the compactness of certain integral operators”, J. Math. Anal. Appl. 68 (1979), 580–594.CrossRefGoogle Scholar
[4]Graham, I. G., ”, in The application and numerical solution of integral equations (eds. Anderssen, R. S., de Hoog, F. R., and Lukas, M. A.) (Alphen aan den Rijn: Sijthoff and Noordhoff, 1980).Google Scholar
[5]Graham, I. G., The numerical solution of Fredholm integral equations of the second kind (Ph. D. Thesis, University of New South Wales, 1980).CrossRefGoogle Scholar
[6]Kantorovich, L. V. and Akilov, G. P., Functional analysis in normed spaces (London/New York: Pergamon, 1964).Google Scholar
[7]Kufner, A., John, O., and Fucik, S., Function spaces (Leyden: Noordhoff International, 1977).Google Scholar
[8]Munteanu, M. J. and Schumaker, L. L., “Direct and inverse theorems for multidimensional spline approximation”, Indiana Univ. Math. J. 23 (1973), 461–470.CrossRefGoogle Scholar
[9]Schneider, C., “Product integration for weakly singular integral equations”, Math. of Comp., to appear.Google Scholar
[10]Sloan, I. H., Noussair, E. and Burn, B. J., “Projection methods for equations of the second kind”, J. Math. Anal. Appl. 69 (1979), 84–103.CrossRefGoogle Scholar