Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sidi, Avram
1985.
Asymptotic Expansions of Mellin Transforms and Analogues of Watson’s Lemma.
SIAM Journal on Mathematical Analysis,
Vol. 16,
Issue. 4,
p.
896.
Sidi, Avram
1986.
Borel Summability and Converging Factors for Some Everywhere Divergent Series.
SIAM Journal on Mathematical Analysis,
Vol. 17,
Issue. 5,
p.
1222.
Weniger, Ernst Joachim
1994.
Nonlinear Numerical Methods and Rational Approximation II.
p.
269.
Lubinsky, D.S.
and
Sidi, A.
2022.
Some biorthogonal polynomials arising in numerical analysis and approximation theory.
Journal of Computational and Applied Mathematics,
Vol. 403,
Issue. ,
p.
113842.

 , where μ
, where μ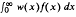 with
with 