Hostname: page-component-6766d58669-h8lrw Total loading time: 0 Render date: 2026-05-21T14:30:56.516Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPLICIT NORDSIECK SECOND DERIVATIVE GENERAL LINEAR METHODS FOR ODES

Part of: Numerical analysis: Ordinary differential equations

Published online by Cambridge University Press:  25 April 2022

P. RAMAZANI Open the ORCID record for P. RAMAZANI [Opens in a new window] ,
A. ABDI Open the ORCID record for A. ABDI [Opens in a new window] ,
G. HOJJATI Open the ORCID record for G. HOJJATI [Opens in a new window]  and
A. MORADI Open the ORCID record for A. MORADI [Opens in a new window]
P. RAMAZANI
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: p.ramazanii@tabrizu.ac.ir, ghojjati@tabrizu.ac.ir, a_moradi@tabrizu.ac.ir
A. ABDI*
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: p.ramazanii@tabrizu.ac.ir, ghojjati@tabrizu.ac.ir, a_moradi@tabrizu.ac.ir
G. HOJJATI
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: p.ramazanii@tabrizu.ac.ir, ghojjati@tabrizu.ac.ir, a_moradi@tabrizu.ac.ir
A. MORADI
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: p.ramazanii@tabrizu.ac.ir, ghojjati@tabrizu.ac.ir, a_moradi@tabrizu.ac.ir
*
e-mail: a_abdi@tabrizu.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with the construction of explicit Nordsieck second derivative general linear methods with s stages of order p with 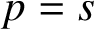$p=s$ and high stage order 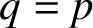$q=p$ with inherent Runge–Kutta or quadratic stability properties. Satisfying the order and stage order conditions together with inherent stability conditions leads to methods with some free parameters, which will be used to obtain methods with a large region of absolute stability. Examples of methods with r external stages and 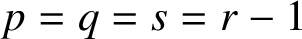$p=q=s=r-1$ up to order five are given, and numerical experiments in a fixed stepsize environment are presented.

Keywords

Nordsieck methodssecond derivative methodsgeneral linear methodsinherent Runge–Kutta stabilityinherent quadratic stability

MSC classification

Primary: 65L05: Initial value problems

Information

Type
Research Article
Information
The ANZIAM Journal , Volume 64 , Issue 1 , January 2022 , pp. 69 - 88
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdi, A., “Construction of high-order quadratically stable second-derivative general linear methods for the numerical integration of stiff ODEs”, J. Comput. Appl. Math. 303 (2016) 218–228; doi:10.1016/j.cam.2016.02.054.CrossRefGoogle Scholar
Abdi, A., Braś, M. and Hojjati, G., “On the construction of second derivative diagonally implicit multistage integration methods”, Appl. Numer. Math. 76 (2014) 1–18; doi:10.1016/j.apnum.2013.08.006.CrossRefGoogle Scholar
Abdi, A. and Butcher, J. C., “Order bounds for second derivative approximations”, BIT 52 (2012) 273–281; doi:10.1007/s10543-011-0361-1.CrossRefGoogle Scholar
Abdi, A. and Conte, C., “Implementation of second derivative general linear methods”, Calcolo 57 (2020) 1–29; doi:10.1007/s10092-020-00370-w.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “An extension of general linear methods”, Numer. Algorithms 57 (2011) 149–167; doi:10.1007/s11075-010-9420-y.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “Maximal order for second derivative general linear methods with Runge–Kutta stability”, Appl. Numer. Math. 61 (2011) 1046–1058; doi:10.1016/j.apnum.2011.06.004.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “Implementation of Nordsieck second derivative methods for stiff ODEs”, Appl. Numer. Math. 94 (2015) 241–253; doi:10.1016/j.apnum.2015.04.002.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “Second derivative backward differentiation formulae for ODEs based on barycentric rational interpolants”, Numer. Algorithms 87 (2021) 1577–1591; doi:10.1007/s11075-020-01020-6.CrossRefGoogle Scholar
Abdi, A., Hojjati, G., Izzo, G. and Jackiewicz, Z., “Global error estimation for explicit general linear methods”, Numer. Algorithms 89 (2022) 1075–1093; doi:10.1007/s11075-021-01146-1.CrossRefGoogle Scholar
Abdi, A. and Jackiewicz, Z., “Towards a code for nonstiff differential systems based on general linear methods with inherent Runge–Kutta stability”, Appl. Numer. Math. 136 (2019) 103–121; doi:10.1016/j.apnum.2018.10.001.CrossRefGoogle Scholar
Barghi Oskouie, N., Hojjati, G. and Abdi, A., “Efficient second derivative methods with extended stability regions for non-stiff IVPs”, Comput. Appl. Math. 37 (2018) 2001–2016; doi:10.1007/s40314-018-0619-1.CrossRefGoogle Scholar
Bartoszewski, Z. and Jackiewicz, Z., “Nordsieck representation of two-step Runge–Kutta methods for ordinary differential equations”, Appl. Numer. Math. 53 (2005) 149–163; doi:10.1016/j.apnum.2004.08.010.CrossRefGoogle Scholar
Braś, M. and Cardone, A., “Construction of efficient general linear methods for non-stiff differential systems”, Math. Model. Anal. 17 (2012) 171–189; doi:10.3846/13926292.2012.655789.CrossRefGoogle Scholar
Butcher, J. C., “On the convergence of numerical solutions to ordinary differential equations”, Math. Comp. 20 (1966) 1–10; doi:10.2307/2004263.CrossRefGoogle Scholar
Butcher, J. C., Numerical methods for ordinary differential equations (Wiley, New York, 2016).CrossRefGoogle Scholar
Butcher, J. C., Chartier, P. and Jackiewicz, Z., “Experiments with a variable-order type 1 DIMSIM code”, Numer. Algorithms 22 (1999) 237–261; doi:10.1023/A:1019135630307.CrossRefGoogle Scholar
Butcher, J. C. and Hojjati, G., “Second derivative methods with RK stability”, Numer. Algorithms 40 (2005) 415–429; doi:10.1007/s11075-005-0413-1.CrossRefGoogle Scholar
Butcher, J. C. and Jackiewicz, Z., “Construction of general linear methods with Runge–Kutta stability properties”, Numer. Algorithms 36 (2004) 53–72; doi:10.1023/B:NUMA.0000027738.54515.50.CrossRefGoogle Scholar
Butcher, J. C. and Wright, W. M., “The construction of practical general linear methods”, BIT 43 (2003) 695–721; doi:10.1023/B:BITN.0000009952.71388.23.CrossRefGoogle Scholar
Cardone, A. and Jackiewicz, Z., “Explicit Nordsieck methods with quadratic stability”, Numer. Algorithms 60 (2012) 1–25; doi:10.1007/s11075-011-9509-y.CrossRefGoogle Scholar
Cash, J. R., “Second derivative extended backward differentiation formulas for the numerical integration of stiff systems”, SIAM J. Numer. Anal. 18 (1981) 21–36; doi:10.1137/0718003.CrossRefGoogle Scholar
Chan, R. P. K. and Tsai, A. Y. J., “On explicit two-derivative Runge–Kutta methods”, Numer. Algorithms 53 (2010) 171–194; doi:10.1007/s11075-009-9349-1.CrossRefGoogle Scholar
Chollom, J. and Jackiewicz, Z., “Construction of two-step Runge–Kutta methods with large regions of absolute stability”, J. Comput. Appl. Math. 157 (2003) 125–137; doi:10.1016/S0377-0427(03)00382-0.CrossRefGoogle Scholar
Constantinescu, E. M., “Generalizing global error estimation for ordinary differential equations by using coupled time-stepping methods”, J. Comput. Appl. Math. 332 (2018) 140–158; doi:10.1016/j.cam.2017.05.012.CrossRefGoogle Scholar
Conte, D., D’Ambrosio, R. and Jackiewicz, Z., “Two-step Runge–Kutta methods with quadratic stability functions”, J. Sci. Comput. 2 (2010) 191–218; doi:10.1007/s10915-010-9378-x.CrossRefGoogle Scholar
Dahlquist, G., “A special stability problem for linear multistep methods”, BIT 3 (1963) 27–43; doi:10.1007/BF01963532.CrossRefGoogle Scholar
Enright, W. H., “Second derivative multistep methods for stiff ordinary differential equations”, SIAM J. Numer. Anal. 11 (1974) 321–331; https://www.jstor.org/stable/2156073.CrossRefGoogle Scholar
Hojjati, G., Rahimi Ardabili, M. Y. and Hosseini, S. M., “New second derivative multistep methods for stiff systems”, Appl. Math. Model. 30 (2006) 466–476; doi:10.1016/j.apm.2005.06.007.CrossRefGoogle Scholar
Jackiewicz, Z., General linear methods for ordinary differential equations (Wiley, New Jersey, 2009).CrossRefGoogle Scholar
Jackiewicz, Z. and Tracogna, S., “A general class of two-step Runge–Kutta methods for ordinary differential equations”, SIAM J. Numer. Anal. 32 (1995) 1390–1427; doi:10.1137/0732064.CrossRefGoogle Scholar
Jackiewicz, Z. and Tracogna, S., “Variable stepsize continuous two-step Runge–Kutta methods for ordinary differential equations”, Numer. Algorithms 12 (1996) 347–368; doi:10.1007/BF02142812.CrossRefGoogle Scholar
Jackiewicz, Z. and Verner, J. H., “Derivation and implementation of two-step Runge–Kutta pairs”, Jpn. J. Ind. Appl. Math. 19 (2002) 227–248; doi:10.1007/BF03167454.CrossRefGoogle Scholar
Kulikov, G., “Cheap global error estimation in some Runge–Kutta pairs”, IMA J. Numer. Anal. 33 (2013) 136–163; doi:10.1093/imanum/drr060.CrossRefGoogle Scholar
Movahedinejad, A., Hojjati, G. and Abdi, A., “Second derivative general linear methods with inherent Runge–Kutta stability”, Numer. Algorithms 73 (2016) 371–389; doi:10.1007/s11075-016-0099-6.CrossRefGoogle Scholar
Movahedinejad, A., Hojjati, G. and Abdi, A., “Construction of Nordsieck second derivative general linear methods with inherent quadratic stability”, Math. Model. Anal. 22 (2017) 60–77; doi:10.3846/13926292.2017.1269024.CrossRefGoogle Scholar
Prothero, A. and Robinson, A., “On the stability and accuracy of one-step methods for solving stiff systems of ordinary differential equations”, Math. Comput. 28 (1974) 145–162; doi:10.2307/2005822.CrossRefGoogle Scholar
Wright, W. M., “Explicit general linear methods with inherent Runge–Kutta stability”, Numer. Algorithms 31 (2002) 381–399; doi:10.1023/A:1021195804379.CrossRefGoogle Scholar
Wright, W. M., “General linear methods with inherent Runge–Kutta stability”, Doctoral Thesis, The University of Auckland, New Zealand, 2002.Google Scholar