Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-05-08T23:01:26.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical Methodology for Large Claims

Published online by Cambridge University Press:  29 August 2014

J. Tiago de Oliveira
J. Tiago de Oliveira*
Affiliation:
Center of Applied Mathematics (I.A.C.) Faculty of Sciences, Lisbon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The question of large claims in insurance is, evidently, a very important one, chiefly if we consider it in relation with reinsurance. To a statistician it seems that it can be approached, essentially, in two different ways.

The first one can be the study of overpassing of a large bound, considered to be a critical one. If N(t) is the Poisson process of events (claims) of intensity v, each claim having amounts Yi, independent and identically distributed with distribution function F(x), the compound Poisson process

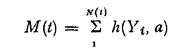
where a denotes the critical level, can describe the behaviour of some problems connected with the overpassing of the critical level. For instance, if h(Y, a) = H(Y − a), where H(x) denotes the Heavside jump function (H(x) = o if x < o, H(x) = 1 if x ≥ o), M(t) is then the number of claims overpassing a; if h(Y, a) = Y H(Y − a), M(t) denotes the total amount of claims exceeding the critical level; if h(Y, a) = (Y − a) H(Y − a), M(t) denotes the total claims reinsured for some reinsurance policy, etc.

Taking the year as unit of time, the random variables M(1), M(2) − M(1), … are evidently independent and identically distributed; its distribution function is easy to obtain through the computation of the characteristic function of M(1). For details see Parzen (1964) and the papers on The ASTIN Bulletin on compound processes; for the use of distribution functions F(x), it seems that the ones developed recently by Pickands III (1975) can be useful, as they are, in some way, pre-asymptotic forms associated with tails, leading easily to the asymptotic distributions of extremes.

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 9 , Issue 1-2 , January 1977 , pp. 1 - 9
Copyright
Copyright © International Actuarial Association 1977

References

Refekences

Beard, R. E., (1963). Some notes on the statistical theory of extreme values, The ASTIN Bull., Vol. III.Google Scholar
Finetti, Bruno de, (1964). La théorie des plus grands valeurs et son application aux problèmes de l'assurance, The ASTIN Bull., Vol. III.Google Scholar
Gnedenko, B. V., (1943). Sur la distribution limite du terme maximum d'une série aléatoire, Ann. Math., Vol. 44.CrossRefGoogle Scholar
Gumbel, E. J., (1935). Les valeurs extrêmes des distributions statistiqucs, Ann. Inst. H. Poincaré, Vol. 4.Google Scholar
Gumbel, E. J., (1958). Statistics of extremes, Columbia University Press.CrossRefGoogle Scholar
Leadbetter, M. R., (1972). Extreme value theory and stochastic processes, Int. Conf. on Structural Safety and Reliability, Pergamon Press.Google Scholar
Lindgren, Georg, (1975). Prediction of catastrophes and high level crossings, presented at Warsow 40th meeting of the International Statistical Institute.Google Scholar
Parzen, E., (1964). Stochastic Processes, Holden-Day Inc.Google Scholar
Pickands, James III, (1975). Statistical inference using extreme order statistics, Ann. Stat., Vol. 3.Google Scholar
Ramachandran, G., (1974). Extreme value theory and large fire losses. The ASTIN Bull., Vol. VII.Google Scholar
Ramachandran, G., (1975). Extreme order statistics in large samples from exponential type distributions and their applications to fire losses, Statistical Distributions in Scientific Work, 2, D. Reidel Publ. Cy.Google Scholar
Tiago de Oliveira, J., (1972). Statistics for Gumbel and Fréchet distributions, Int. Conf. on Structural Safety and Reliability, Pergamon Press.Google Scholar
Tiago de Ouveira, J., (1975). Statistical decision for univariate extremes, to be publ. in Trab. Estad. y Invest. Oper.Google Scholar