Article contents
THE COLLAPSE OF THE HILBERT PROGRAM: A VARIATION ON THE GÖDELIAN THEME
Published online by Cambridge University Press: 23 March 2022
Abstract
The Hilbert program was actually a specific approach for proving consistency, a kind of constructive model theory. Quantifiers were supposed to be replaced by ε-terms. εxA(x) was supposed to denote a witness to 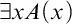 $\exists xA(x)$, or something arbitrary if there is none. The Hilbertians claimed that in any proof in a number-theoretic system S, each ε-term can be replaced by a numeral, making each line provable and true. This implies that S must not only be consistent, but also 1-consistent (
$\exists xA(x)$, or something arbitrary if there is none. The Hilbertians claimed that in any proof in a number-theoretic system S, each ε-term can be replaced by a numeral, making each line provable and true. This implies that S must not only be consistent, but also 1-consistent (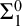 ${\Sigma}_1^0$-correct). Here we show that if the result is supposed to be provable within S, a statement about all
${\Sigma}_1^0$-correct). Here we show that if the result is supposed to be provable within S, a statement about all 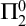 ${\Pi}_2^0$ statements that subsumes itself within its own scope must be provable, yielding a contradiction. The result resembles Gödel’s but arises naturally out of the Hilbert program itself.
${\Pi}_2^0$ statements that subsumes itself within its own scope must be provable, yielding a contradiction. The result resembles Gödel’s but arises naturally out of the Hilbert program itself.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
Footnotes
This paper is based on a transcript of a lecture given at Indiana University on October 15, 2007 in honor of the inauguration of President Michael A. McRobbie. An abstract of another version of this talk (given at the 2008 Winter Meeting of the Association for Symbolic Logic on December 30, 2008) was published in The Bulletin of Symbolic Logic, vol. 15 (2009), no. 2, pp. 229–231.
References
- 1
- Cited by


