Computability theoretic aspects of Polish metric spaces are studied by adapting notions and methods of computable structure theory. In this dissertation, we mainly investigate index sets and classification problems for computably presentable Polish metric spaces. We find the complexity of a number of index sets, isomorphism problems, and embedding problems for computably presentable metric spaces. We also provide several computable structure theory results related to some classical Polish metric spaces such as the Urysohn space 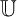$\mathbb {U}$, the Cantor space 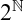$2^{\mathbb {N}}$, the Baire space 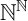$\mathbb {N}^{\mathbb {N}}$, and spaces of continuous functions.

Abstract prepared by Teerawat Thewmorakot.

E-mail: teerawat.thew@hotmail.com