Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-12T21:58:16.715Z Has data issue: false hasContentIssue false
  • English
  • Français

A RECONSTRUCTION OF STEEL’S MULTIVERSE PROJECT

Part of: Set theory Philosophical aspects of logic and foundations General and miscellaneous specific topics

Published online by Cambridge University Press:  11 June 2020

PENELOPE MADDY  and
TOBY MEADOWS
PENELOPE MADDY
Affiliation:
DEPARTMENT OF LOGIC AND PHILOSOPHY OF SCIENCE UNIVERSITY OF CALIFORNIA, IRVINEIRVINE, CA, USA E-mail: pjmaddy@uci.edu E-mail: meadowst@uci.edu
TOBY MEADOWS
Affiliation:
DEPARTMENT OF LOGIC AND PHILOSOPHY OF SCIENCE UNIVERSITY OF CALIFORNIA, IRVINEIRVINE, CA, USA E-mail: pjmaddy@uci.edu E-mail: meadowst@uci.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper reconstructs Steel’s multiverse project in his ‘Gödel’s program’ (Steel, 2014), first by comparing it to those of Hamkins (2012) and Woodin (2011), then by detailed analysis what’s presented in Steel’s brief text. In particular, we reconstruct his notion of a ‘natural’ theory, describe his multiverse axioms and his translation function, and assess the resulting status of the Continuum Hypothesis. In the end, we reconceptualize the defect that Steel thinks 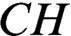$CH$ might suffer from and isolate what it would take to remove it while working within his framework. As our goal is to present as coherent and compelling a philosophical and mathematical story as we can, we allow ourselves to augment Steel’s story in places (e.g., in the treatment of Amalgamation) and to depart from it in others (e.g., the removal of ‘meaning’ from the account). The relevant mathematics is laid out in the appendices.

Keywords

philosophy of mathematicsfoundations of mathematicsset theorycontinuum hypothesislarge cardinalsforcinggeneric multiverse

MSC classification

Primary: 00A30: Philosophy of mathematics
Secondary: 00A35: Methodology of mathematics, didactics 03A05: Philosophical and critical 03E50: Continuum hypothesis and Martin's axiom 03E55: Large cardinals 03E65: Other hypotheses and axioms
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 26 , Issue 2 , June 2020 , pp. 118 - 169
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

REFERENCES

Balaguer, M., Platonism and Anti-Platonism in Mathematics , Oxford University Press, New York, 1998.Google Scholar
Cantor, G., Contributions to the Founding of the Theory of Transfinite Numbers. LaSalle, IL: Open Court 1952. Translated by Philip Jourdain.Google Scholar
Corazza, P., Forcing with non-wellfounded models . The Australasian Journal of Logic , vol. 5 (2007), pp. 20–58.CrossRefGoogle Scholar
Feferman, S., Why the programs for new axioms need to be questioned , this Journal, vol. 4 (2000), pp. 401–413.Google Scholar
Foreman, M. and Kanamori, A., Handbook of Set Theory , Springer, Netherlands, 2009.Google Scholar
Friedman, S. D., Fine Structure and Class Forcing . De Gruyter Series in Logic and Its Applications, Walter de Gruyter, Berlin, 2000.CrossRefGoogle Scholar
Fuchs, G., Hamkins, J. D., and Reitz, J., Set-theoretic geology . Annals of Pure and Applied Logic , vol. 166 (2015), no. 4, pp. 464–501.CrossRefGoogle Scholar
Gödel, K., What is cantor’s continuum problem? , Collected Papers, vol. II (Feferman, S., et al., editors), Oxford University Press, Oxford, 1990, pp. 176–187, 254–270.Google Scholar
Hamkins, J. D., The set-theoretic multiverse . Review of Symbolic Logic , vol. 5 (2012), no. 3, pp. 416–449.CrossRefGoogle Scholar
Hamkins, J. D., Upward closure and amalgamation in the generic multiverse of a countable model of set theory, 2015, arXiv e-prints.Google Scholar
Hilbert, D., On the infinite , From Frege to Gödel (van Heijenoort, J., editor), Harvard University Press, Cambridge, 1967, pp. 369–392.Google Scholar
Jech, T., Set Theory , Springer, Heidelberg, 2003.Google Scholar
Jech, T., Magidor, M., Mitchell, W., and Prikry, K., Precipitous ideals . The Journal of Symbolic Logic , vol. 45 (1980), no. 1, pp. 1–8.CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings , Springer, New York, 2003.Google Scholar
Koellner, P., Large cardinals and determinacy , The Stanford Encyclopedia of Philosophy (Zalta, E. N., editor), Springer, New York, 2014. Available at https://plato.stanford.edu/archives/spr2014/entries/large-cardinals-determinacy/.Google Scholar
Kunen, K., Set Theory: An Introduction to Independence Proofs , Elsevier, Amsterdam, 2006.Google Scholar
Kunen, K., Set Theory , second ed., College Publications, London, 2011.Google Scholar
Levy, A. and Solovay, R., Measurable cardinals and the continuum hypothesis . Israel Journal of Mathematics , vol. 5 (1967), pp. 234–248.CrossRefGoogle Scholar
Maddy, P., Defending the Axioms , Oxford University Press, Oxford, 2011.CrossRefGoogle Scholar
Maddy, P., Set-theoretic foundations , Foundations of Mathematics (Caicedo, A., et al., editors), American Mathematical Society, Providence, 2017, pp. 289–322.CrossRefGoogle Scholar
Magidor, M., Some set theories are more equal, 2019. Available at http://logic.harvard.edu/efi.php#multimedia.Google Scholar
Martin, D. A., Completeness or incompleteness of basic mathematical concepts, 2019. Available at http://www.math.ucla.edu/dam/booketc/efi.pdf.Google Scholar
Martin, D. A., Hilbert’s first problem: The continuum hypothesis , Mathematical Developments from Hilbert’s Problems (Browder, F., editor), Proceedings of Symposia in Pure Mathematics, vol. 28, American Mathematical Society, Providence, RI, 1976, pp. 81–92.CrossRefGoogle Scholar
Meadows, T., Two arguments against the generic multiverse . Review of Symbolic Logic (2020), forthcoming.Google Scholar
Moore, G. Towards a history of cantor’s continuum problem , The History of Modern Mathematics, vol. I (Rowe, D. and McCleary, J., editors), Academic Press, Cambridge, 1989, pp. 79–121.Google Scholar
Moschovakis, Y., Descriptive Set Theory , second ed., American Mathematical Society, Providence, RI, 2009.CrossRefGoogle Scholar
Reitz, J., The ground axiom . Journal of Symbolic Logic , vol. 72 (2007), no. 4, pp. 1299–1317.CrossRefGoogle Scholar
Schatz, J., Axiom Selection and Maximize: Forcing Axioms vs. V=Ultimate-L , UCI Ph.D. dissertation, 2019.Google Scholar
Shelah, S., Can you take solovay’s inaccessible away? Israel Journal of Mathematics , vol. 48 (1984), no. 1, pp. 1–47.CrossRefGoogle Scholar
Solovay, R. M., A model of set-theory in which every set of reals is Lebesgue measurable . Annals of Mathematics , vol. 92 (1970), no. 1, pp. 1–56.CrossRefGoogle Scholar
Steel, J., Mathematics needs new axioms, this Journal, vol. 6 (2000), pp. 422–433.Google Scholar
Steel, J., Gödel’s program , Interpreting Gödel: Critical Essays (Kennedy, J., editor), Cambridge University Press, Cambridge, 2014, pp. 153–179.CrossRefGoogle Scholar
Steel, J., Ordinal definability in models of determinacy , Ordinal Definability and Recursion Theory (Kechris, B. L. A. and Steel, J., editors), Cambridge University Press, Cambridge, 2016, pp. 3–48.CrossRefGoogle Scholar
Todorcevic, S., The power set of omega-1 and the continuum problem, 2019. Available at http://logic.harvard.edu/efi.php#multimedia.Google Scholar
Usuba, T., The downward directed grounds hypothesis and very large cardinals . Journal of Mathematical Logic , vol. 17 (2017), p. 2.CrossRefGoogle Scholar
Weaver, N., Forcing for Mathematicians , World Scientific, Singapore, 2014.CrossRefGoogle Scholar
Woodin, H., In search of ultimate-l, this Journal, vol. 23 (2017), pp. 1–109.Google Scholar
Woodin, H., The continuum hypothesis, the generic-multiverse of sets, and the omega conjecture , Set Theory, Arithmetic, and the Foundations of Mathematics (Kennedy, J. and Kossak, R., editors), Cambridge University Press, Cambridge, 2011, pp. 13–42.CrossRefGoogle Scholar