No CrossRef data available.
Towards Finding a Lattice that Characterizes the 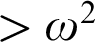 ${>}\ \omega ^2$-Fickle Recursively Enumerable Turing Degrees
${>}\ \omega ^2$-Fickle Recursively Enumerable Turing Degrees
Published online by Cambridge University Press: 28 February 2022
Abstract
Given a finite lattice L that can be embedded in the recursively enumerable (r.e.) Turing degrees  $\langle \mathcal {R}_{\mathrm {T}},\leq _{\mathrm {T}}\rangle $, we do not in general know how to characterize the degrees
$\langle \mathcal {R}_{\mathrm {T}},\leq _{\mathrm {T}}\rangle $, we do not in general know how to characterize the degrees 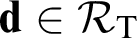 $\mathbf {d}\in \mathcal {R}_{\mathrm {T}}$ below which L can be bounded. The important characterizations known are of the
$\mathbf {d}\in \mathcal {R}_{\mathrm {T}}$ below which L can be bounded. The important characterizations known are of the 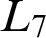 $L_7$ and
$L_7$ and 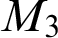 $M_3$ lattices, where the lattices are bounded below
$M_3$ lattices, where the lattices are bounded below 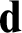 $\mathbf {d}$ if and only if
$\mathbf {d}$ if and only if 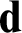 $\mathbf {d}$ contains sets of “fickleness”
$\mathbf {d}$ contains sets of “fickleness”  $>\omega $ and
$>\omega $ and 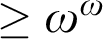 $\geq \omega ^\omega $ respectively. We work towards finding a lattice that characterizes the levels above
$\geq \omega ^\omega $ respectively. We work towards finding a lattice that characterizes the levels above 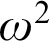 $\omega ^2$, the first non-trivial level after
$\omega ^2$, the first non-trivial level after  $\omega $. We introduced a lattice-theoretic property called “
$\omega $. We introduced a lattice-theoretic property called “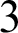 $3$-directness” to describe lattices that are no “wider” or “taller” than
$3$-directness” to describe lattices that are no “wider” or “taller” than 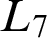 $L_7$ and
$L_7$ and 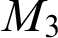 $M_3$. We exhaust the 3-direct lattices L, but they turn out to also characterize the
$M_3$. We exhaust the 3-direct lattices L, but they turn out to also characterize the 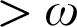 $>\omega $ or
$>\omega $ or 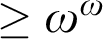 $\geq \omega ^\omega $ levels, if L is not already embeddable below all non-zero r.e. degrees. We also considered upper semilattices (USLs) by removing the bottom meet(s) of some 3-direct lattices, but the removals did not change the levels characterized. This leads us to conjecture that a USL characterizes the same r.e. degrees as the lattice on which the USL is based. We discovered three 3-direct lattices besides
$\geq \omega ^\omega $ levels, if L is not already embeddable below all non-zero r.e. degrees. We also considered upper semilattices (USLs) by removing the bottom meet(s) of some 3-direct lattices, but the removals did not change the levels characterized. This leads us to conjecture that a USL characterizes the same r.e. degrees as the lattice on which the USL is based. We discovered three 3-direct lattices besides 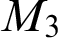 $M_3$ that also characterize the
$M_3$ that also characterize the 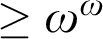 $\geq \omega ^\omega $-levels. Our search for a
$\geq \omega ^\omega $-levels. Our search for a 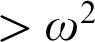 $>\omega ^2$-candidate therefore involves the lattice-theoretic problem of finding lattices that do not contain any of the four
$>\omega ^2$-candidate therefore involves the lattice-theoretic problem of finding lattices that do not contain any of the four 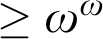 $\geq \omega ^\omega $-lattices as sublattices.
$\geq \omega ^\omega $-lattices as sublattices.
Abstract prepared by Liling Ko.
E-mail: ko.390@osu.edu
MSC classification
Information
- Type
- Thesis Abstracts
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Association for Symbolic Logic
Footnotes
Supervised by Peter Cholak.


