Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-11T06:55:11.498Z Has data issue: false hasContentIssue false
  • English
  • Français

AN UPPER BOUND ON THE LENGTH OF AN ALGEBRA AND ITS APPLICATION TO THE GROUP ALGEBRA OF THE DIHEDRAL GROUP

Part of: Rings and algebras arising under various constructions Representation theory of groups

Published online by Cambridge University Press:  10 February 2025

M. A. KHRYSTIK Open the ORCID record for M. A. KHRYSTIK [Opens in a new window]
M. A. KHRYSTIK*
Affiliation:
Faculty of Computer Science, HSE University, Moscow 101000, Russia and Moscow Center of Fundamental and Applied Mathematics, Moscow 119991, Russia
*
e-mail: good_michael@mail.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 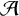${\mathcal {A}}$ be a unital 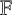${\mathbb {F}}$-algebra and let 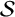${\mathcal {S}}$ be a generating set of 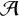${\mathcal {A}}$. The length of 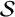${\mathcal {S}}$ is the smallest number k such that 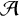${\mathcal {A}}$ equals the 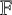${\mathbb {F}}$-linear span of all products of length at most k of elements from 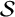${\mathcal {S}}$. The length of 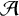${\mathcal {A}}$, denoted by 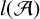$l({\mathcal {A}})$, is defined to be the maximal length of its generating sets. We show that 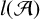$l({\mathcal {A}})$ does not exceed the maximum of 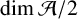$\dim {\mathcal {A}} / 2$ and 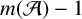$m({\mathcal {A}})-1$, where 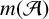$m({\mathcal {A}})$ is the largest degree of the minimal polynomial among all elements of the algebra 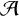${\mathcal {A}}$. As an application, we show that for arbitrary odd n, the length of the group algebra of the dihedral group of order 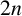$2n$ equals n.

Keywords

finite-dimensional algebraslength of an algebragroup algebrasdihedral grouprepresentations of dihedral groups

MSC classification

Primary: 16S34: Group rings , Laurent polynomial rings
Secondary: 20C05: Group rings of finite groups and their modules 20C30: Representations of finite symmetric groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by Russian Science Foundation, grant 20-11-20203.

References

Guterman, A. E., Khrystik, M. A. and Markova, O. V., ‘On the lengths of group algebras of finite abelian groups in the modular case’, J. Algebra Appl. 21(6) (2022), 2250117–2250130.CrossRefGoogle Scholar
Guterman, A. E. and Markova, O. V., ‘The length of group algebras of small-order groups’, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. 472 (2018), 76–87; English transl. in J. Math. Sci. 240(6) (2019), 754–761.Google Scholar
Guterman, A. E. and Markova, O. V., ‘The length of the group algebra of the group ${\mathbf{Q}}_8$ ’, in: New Trends in Algebra and Combinatorics. Proceedings of the 3rd International Congress in Algebra and Combinatorics (eds. Shum, K. P., Zelmanov, E., Kolesnikov, P. and Wong, A.) (World Scientific, Singapore, 2019), 106–134.Google Scholar
Guterman, A. E., Markova, O. V. and Khrystik, M. A., ‘On the lengths of group algebras of finite abelian groups in the semi-simple case’, J. Algebra Appl. 21(7) (2022), 2250140–2250153.CrossRefGoogle Scholar
Khrystik, M. A., ‘Length of the group algebra of the direct product of a cyclic group and a cyclic $p$ -group in the modular case’, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 524 (2023), 166–176; English transl. in J. Math. Sci. 281(2) (2024), 334–341.Google Scholar
Khrystik, M. A. and Markova, O. V., ‘The length of the group algebra of the dihedral group of order ${2}^k$ ’, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 496 (2020), 169–181; English transl. in J. Math. Sci. (N. Y.) 255(3) (2021), 324–331.Google Scholar
Khrystik, M. A. and Markova, O. V., ‘On the length of the group algebra of the dihedral group in the semi-simple case’, Commun Algebra 50(5) (2022), 2223–2232.CrossRefGoogle Scholar
Markova, O. V., ‘The length function and matrix algebras’, Fundam. Prikl. Mat. 17(6) (2012), 65–173; English transl. in J. Math. Sci. 193(5) (2013), 687–768.Google Scholar
Markova, O. V., ‘An example of length computation for a group algebra of a noncyclic abelian group in the modular case’, Fundam. Prikl. Mat. 23(2) (2020), 217–229; English transl. in J. Math. Sci. 262(5) (2022), 740–748.Google Scholar
Pappacena, C. J., ‘An upper bound for the length of a finite-dimensional algebra’, J. Algebra 197 (1997), 535–545.CrossRefGoogle Scholar
Paz, A., ‘An application of the Cayley–Hamilton theorem to matrix polynomials in several variables’, Linear Multilinear Algebra 15 (1984), 161–170.CrossRefGoogle Scholar