Hostname: page-component-5d84bcc8dc-qqc7b Total loading time: 0 Render date: 2026-09-08T17:20:24.016Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON AN ASYMPTOTIC VERSION OF A PROBLEM OF MAHLER

Part of: Series expansions Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  15 September 2022

RICARDO FRANCISCO Open the ORCID record for RICARDO FRANCISCO [Opens in a new window]  and
DIEGO MARQUES Open the ORCID record for DIEGO MARQUES [Opens in a new window]
RICARDO FRANCISCO
Affiliation:
Departamento de Matemática, Universidade de Brasília, Brasília, DF, Brazil e-mail: r.f.d.silva@mat.unb.br
DIEGO MARQUES*
Affiliation:
Departamento de Matemática, Universidade de Brasília, Brasília, DF, Brazil
*
e-mail: diego@mat.unb.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for any infinite sets of nonnegative integers 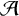$\mathcal {A}$ and 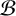$\mathcal {B}$, there exist transcendental analytic functions $f\in \mathbb {Z}\{z\}$ whose coefficients vanish for any indexes 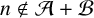$n\not \in \mathcal {A}+\mathcal {B}$ and for which 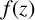$f(z)$ is algebraic whenever z is algebraic and 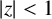$|z|<1$. As a consequence, we provide an affirmative answer for an asymptotic version of Mahler’s problem A.

Keywords

Mahler problemtranscendental functionnatural asymptotic density

MSC classification

Primary: 11J81: Transcendence (general theory)
Secondary: 30B10: Power series (including lacunary series)

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 3 , June 2023 , pp. 398 - 402
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The authors are supported by National Council for Scientific and Technological Development, CNPq.

References

Iwaniec, H. and Kowalski, E., Analytic Number Theory, Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2021).Google Scholar
Mahler, K., Lectures on Transcendental Numbers, Lecture Notes in Mathematics, 546 (Springer-Verlag, Berlin, 1976).CrossRefGoogle Scholar
Marques, D. and Moreira, C. G., ‘A positive answer for a question proposed by K. Mahler’, Math. Ann. 367 (2017), 1059–1062.CrossRefGoogle Scholar
Marques, D. and Moreira, C. G., ‘A note on a complete solution of a problem posed by K. Mahler’, Bull. Aust. Math. Soc. 98 (2018), 60–63.CrossRefGoogle Scholar
Marques, D. and Moreira, C. G., ‘On the exceptional set of transcendental functions with integer coefficients in a prescribed set: the problems $A$ and $C$ of Mahler’, J. Number Theory 218 (2021), 272–287.CrossRefGoogle Scholar
Moreira, J., Richter, F. and Robertson, D., ‘A proof of a sumset conjecture of Erdős’, Ann. of Math. (2) 189 (2019), 605–652.CrossRefGoogle Scholar
Waldschmidt, M., ‘Algebraic values of analytic functions’, Proceedings of the International Conference on Special Functions and their Applications (Chennai, 2002) (eds. Jagannathan, R., Kanemitsu, S., Vanden Berghe, G. and Van Assche, W.). J. Comput. Appl. Math. 160 (2003), 323–333.CrossRefGoogle Scholar