Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T15:18:31.850Z Has data issue: false hasContentIssue false
  • English
  • Français

PARTITIONS OF 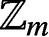$\mathbb {Z}_m$ WITH IDENTICAL REPRESENTATION FUNCTION

Part of: Sequences and sets

Published online by Cambridge University Press:  22 September 2020

SHI-QIANG CHEN Open the ORCID record for SHI-QIANG CHEN [Opens in a new window]  and
XIAO-HUI YAN Open the ORCID record for XIAO-HUI YAN [Opens in a new window]
SHI-QIANG CHEN*
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing210023, P. R. China
XIAO-HUI YAN
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu210023, P. R. China e-mail: yanxiaohui_1992@163.com
*
e-mail: csq20180327@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For a given set 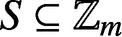$S\subseteq \mathbb {Z}_m$ and 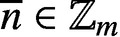$\overline {n}\in \mathbb {Z}_m$ , let 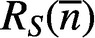$R_S(\overline {n})$ denote the number of solutions of the equation 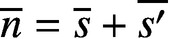$\overline {n}=\overline {s}+\overline {s'}$ with ordered pairs 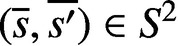$(\overline {s},\overline {s'})\in S^2$ . We determine the structure of 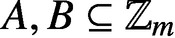$A,B\subseteq \mathbb {Z}_m$ with 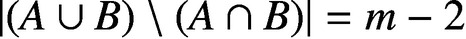$|(A\cup B)\setminus (A\cap B)|=m-2$ such that 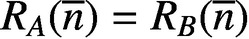$R_{A}(\overline {n})=R_{B}(\overline {n})$ for all 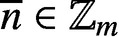$\overline {n}\in \mathbb {Z}_m$ , where m is an even integer.

Keywords

partitionrepresentation function

MSC classification

Primary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 204 - 209
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the National Natural Science Foundation of China, Grant No. 11771211. The first author is also supported by the Project of Graduate Education Innovation of Jiangsu Province, Grant No. KYCX20_1167.

References

Chen, Y. G. and Lev, V. F., ‘Integer sets with identical representation functions’, Integers 16 (2016), Article ID A36, 4 pages.Google Scholar
Chen, Y. G. and Tang, M., ‘Partitions of natural numbers with the same representation functions’, J. Number Theory 129 (2009), 2689–2695.CrossRefGoogle Scholar
Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103 (2002), 137–146.CrossRefGoogle Scholar
Kiss, S. Z. and Sándor, C., ‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161.CrossRefGoogle Scholar
Lev, V. F., ‘Reconstructing integer sets from their representation functions’, Electron. J. Combin. 11 (2004), Article ID R78, 6 pages.CrossRefGoogle Scholar
Li, J. W. and Tang, M., ‘Partitions of the set of nonnegative integers with the same representation functions’, Bull. Aust. Math. Soc. 97 (2018), 200–206.CrossRefGoogle Scholar
Sándor, C., ‘Partitions of natural numbers and their representation functions’, Integers 4 (2004), Article ID A18, 5 pages.Google Scholar
Tang, M., ‘Partitions of the set of natural numbers and their representation functions’, Discrete Math. 308 (2008), 2614–2616.CrossRefGoogle Scholar
Tang, M., ‘Partitions of natural numbers and their representation functions’, Chinese Ann. Math. Ser A 37 (2016), 41–46; English translation, Chinese J. Contemp. Math. 37 (2016), 39–44.Google Scholar
Yang, Q. H. and Chen, F. J. ‘Partitions of ${\mathbb{Z}}_m$with the same representation functions’, Austral. J. Combin. 53 (2012), 257–262.Google Scholar
Yang, Q. H. and Tang, M., ‘Representation functions on finite sets with extreme symmetric differences’, J. Number Theory 180 (2017), 73–85.CrossRefGoogle Scholar