Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T10:30:54.375Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVELY AMENABLE ACTIONS OF THOMPSON’S GROUPS

Part of: Abstract harmonic analysis Selfadjoint operator algebras

Published online by Cambridge University Press:  03 November 2021

EDUARDO SCARPARO Open the ORCID record for EDUARDO SCARPARO [Opens in a new window]
EDUARDO SCARPARO*
Affiliation:
Department of Mathematics, Federal University of Santa Catarina, Florianópolis, Santa Catarina 88040-900, Brazil
*
e-mail: eduardo.scarparo@posgrad.ufsc.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the notion of relatively amenable topological action and show that the action of Thompson’s group T on 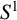$S^1$ is relatively amenable with respect to Thompson’s group F. We use this to conclude that F is exact if and only if T is exact. Moreover, we prove that the groupoid of germs of the action of T on 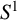$S^1$ is Borel amenable.

Keywords

relatively amenable actionsThompson’s groupsKirchberg algebrauniversal coefficient theoremgroupoid of germs

MSC classification

Primary: 43A07: Means on groups, semigroups, etc.; amenable groups
Secondary: 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 1 , August 2022 , pp. 144 - 150
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C. and Renault, J., Amenable Groupoids, L’Enseignement Mathématique, 36 (Université de Genève, Genève, 2000).Google Scholar
Barlak, S. and Li, X., ‘Cartan subalgebras and the UCT problem’, Adv. Math. 316 (2017), 748–769.Google Scholar
Brix, K. A. and Scarparo, E., ‘C*-simplicity and representations of topological full groups of groupoids’, J. Funct. Anal. 277(9) (2019), 2981–2996.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., C*-Algebras and Finite-Dimensional Approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R., ‘Introductory notes on Richard Thompson’s groups’, Enseign. Math. (2) 42(3–4) (1996), 215–256.Google Scholar
Caprace, P.-E. and Monod, N., ‘Relative amenability’, Groups Geom. Dyn. 8(3) (2014), 747–774.CrossRefGoogle Scholar
Kalantar, M. and Scarparo, E., ‘Boundary maps, germs and quasi-regular representations’, Preprint, 2021, arXiv:2010.02536.CrossRefGoogle Scholar
Kwaśniewski, B. K. and Meyer, R., ‘Essential crossed products for inverse semigroup actions: simplicity and pure infiniteness’, Doc. Math. 26 (2021), 271–335.CrossRefGoogle Scholar
Monod, N., ‘An invitation to bounded cohomology’, Proc. Int. Congress Math., Madrid, Spain, 22–30 August 2006, Vol. II (European Mathematical Society, Zurich, 2006), 1183–1211.Google Scholar
Nyland, P. and Ortega, E., ‘Topological full groups of ample groupoids with applications to graph algebras’, Int. J. Math. 30(4) (2019), Article no. 1950018, 66 pages.CrossRefGoogle Scholar
Ozawa, N., ‘Boundary amenability of relatively hyperbolic groups’, Topology Appl. 153(14) (2006), 2624–2630.CrossRefGoogle Scholar
Renault, J., A Groupoid Approach to C*-Algebras, Lecture Notes in Mathematics, 793 (Springer, Cham, 1980).CrossRefGoogle Scholar
Renault, J., ‘Topological amenability is a Borel property’, Math. Scand. 117(1) (2015), 5–30.CrossRefGoogle Scholar
Spielberg, J., ‘Graph-based models for Kirchberg algebras’, J. Operator Theory 57(2) (2007), 347–374.Google Scholar