Article contents
SOME CRITERIA FOR SOLVABILITY AND NILPOTENCY OF FINITE GROUPS BY STRONGLY MONOLITHIC CHARACTERS
Published online by Cambridge University Press: 22 September 2022
Abstract
Gagola and Lewis [‘A character theoretic condition characterizing nilpotent groups’, Comm. Algebra 27 (1999), 1053–1056] proved that a finite group G is nilpotent if and only if 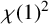 $\chi (1)^{2}$ divides
$\chi (1)^{2}$ divides 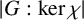 $\lvert G:\textrm {ker}\,\chi \rvert $ for every irreducible character
$\lvert G:\textrm {ker}\,\chi \rvert $ for every irreducible character 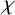 $\chi $ of G. The theorem was later generalised by using monolithic characters. We generalise the theorem further considering only strongly monolithic characters. We also give some criteria for solvability and nilpotency of finite groups by their strongly monolithic characters.
$\chi $ of G. The theorem was later generalised by using monolithic characters. We generalise the theorem further considering only strongly monolithic characters. We also give some criteria for solvability and nilpotency of finite groups by their strongly monolithic characters.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 120 - 124
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The work of the authors was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK), project number 119F295.
References
- 2
- Cited by


