Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T16:49:37.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Circular colouring and graph homomorphism

Published online by Cambridge University Press:  17 April 2009

Xuding zhu
Xuding zhu
Affiliation:
Department of Applied Mathematics, National Sun Yat-sen University, Kaohsiung, Taiwan 80424 e-mail: zhu@math.nsysu.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any pair of integers p, q such that (p, q) = 1 and p ≥ 2q, the graph 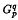has vertices {0, 1, …, p − 1} and edges {ij: q ≤ |i − j| ≤ p − q}. These graphs play the same role in the study of circular chromatic number as that played by the complete graphs in the study of chromatic number. The graphs 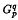share many properties of the complete graphs. However, there are also striking differences between the graphs 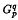and the complete graphs. We shall prove in this paper that for many pairs of integers p, q, one may delete most of the edges of 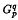so that the resulting graph still has circular chromatic number p/q. To be precise, we shall prove that for any number r < 2, there exists a rational number p/q (where (p, q) = 1) which is less than r but arbitrarily close to r, such that 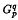contains a subgraph H with 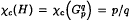and 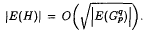. This is in sharp contrast to the fact that the complete graphs are edge critical, that is, the deletion of any edge will decrease its chromatic number and its circular chromatic number.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 59 , Issue 1 , February 1999 , pp. 83 - 97
Copyright
Copyright © Australian Mathematical Society 1999

References

[1]Abbott, H.L. and Zhou, B., ‘The star chromatic number of a graph’, J. Graph Theory 17 (1993), 349–360.CrossRefGoogle Scholar
[2]Bondy, J.A. and Hell, P., ‘A note on the star chromatic number’, J. Graph Theory 14 (1990), 479–482.CrossRefGoogle Scholar
[3]Duffus, D. and Sauer, N., ‘Lattice arising in categorical investigations of Hedetniemi's conjecture’, Discrete Math. 152 (1996), 125–139.CrossRefGoogle Scholar
[4]Guichard, D.R., ‘Acyclic graph coloring and the complexity of the star chromatic number’, J. Graph Theory 17 (1993), 129–134.CrossRefGoogle Scholar
[5]Moser, D., ‘The star-chromatic number of planar graphs’, J. Graph Theory 24 (1997), 33–43.3.0.CO;2-K>CrossRefGoogle Scholar
[6]Neˇsetřil, J. and Zhu, X., ‘Path homomorphisms’, Math. Proc. Cambridge Philos. Soc. 120 (1996), 207–220.CrossRefGoogle Scholar
[7]Steffen, E. and Zhu, X., ‘On the star chromatic numbers of graphs’, Combinatorica 16 (1996), 439–448.CrossRefGoogle Scholar
[8]Tardif, C., ‘Fractional multiples of graphs and the density of vertex-transitive graphs’, (preprint).Google Scholar
[9]Vince, A., ‘Star chromatic number’, J. Graph Theory 12 (1988), 551–559.CrossRefGoogle Scholar
[10]Welzl, E., ‘Color-families are dense’, J. Theoret. Comput. Sci. 17 (1982), 29–41.CrossRefGoogle Scholar
[11]Welzl, E., ‘Symmetric graphs and interpretations’, J. Combin. Theory Ser. B 37 (1984), 235–244.CrossRefGoogle Scholar
[12]Zhu, X., ‘Star chromatic numbers and products of graphs’, J. Graph Theory 16 (1992), 557–569.CrossRefGoogle Scholar
[13]Zhu, X., ‘Uniquely H-colorable graphs with large girth’, J. Graph Theory 23 (1996), 33–41.3.0.CO;2-L>CrossRefGoogle Scholar
[14]Zhu, X., ‘Construction of uniquely H-colorable graphs’, J. Graph Theory (to appear).Google Scholar
[15]Zhu, X., ‘Planar graphs with circular chromatic numbers between 3 and 4’, (preprint).Google Scholar
[16]Zhu, X., ‘Circular chromatic number, a survey’, (preprint).Google Scholar