Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-30T18:09:37.287Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREE OF THE 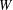$W$-OPERATOR AND NONCROSSING PARTITIONS

Part of: Combinatorics Algebraic combinatorics

Published online by Cambridge University Press:  23 October 2019

HAO SUN Open the ORCID record for HAO SUN [Opens in a new window]
HAO SUN*
Affiliation:
Department of Mathematics, Sun Yat-Sen University, 135 Xingang W Rd, BinJiang Lu, Haizhu Qu, Guangzhou Shi, Guangdong Sheng, China email sunh66@mail.sysu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The 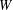$W$-operator, 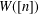$W([n])$, generalises the cut-and-join operator. We prove that 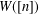$W([n])$ can be written as the sum of 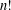$n!$ terms, each term corresponding uniquely to a permutation in 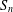$S_{\!n}$. We also prove that there is a correspondence between the terms of 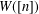$W([n])$ with maximal degree and noncrossing partitions.

Keywords

W-operatorcut-and-join operatorpermutationnoncrossing partition

MSC classification

Primary: 05E15: Combinatorial aspects of groups and algebras
Secondary: 05A18: Partitions of sets

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 186 - 200
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

References

Goulden, I. P., ‘A differential operator for symmetric functions and the combinatorics of multiplying transpositions’, Trans. Amer. Math. Soc. 344(1) (1994), 421–440.Google Scholar
Goulden, I. P. and Jackson, D. M., ‘Transitive factorisations into transpositions and holomorphic mappings on the sphere’, Proc. Amer. Math. Soc. 125(1) (1997), 51–60.Google Scholar
Goulden, I. P. and Jackson, D. M., ‘A proof of a conjecture for the number of ramified coverings of the sphere by the torus’, J. Combin. Theory Ser. A 88(2) (1999), 246–258.Google Scholar
Goulden, I. P. and Jackson, D. M., ‘The number of ramified coverings of the sphere by the double torus, and a general form for higher genera’, J. Combin. Theory Ser. A 88(2) (1999), 259–275.Google Scholar
Goulden, I. P. and Jackson, D. M., ‘Transitive factorizations in the symmetric group, and combinatorial aspects of singularity theory’, Eur. J. Combin. 21(8) (2000), 1001–1016.Google Scholar
Goulden, I. P., Jackson, D. M. and Vainshtein, A., ‘The number of ramified coverings of the sphere by the torus and surfaces of higher genera’, Ann. Combin. 4(1) (2000), 27–46.Google Scholar
Goulden, I. P., Jackson, D. M. and Vakil, R., ‘Towards the geometry of double Hurwitz numbers’, Adv. Math. 198(1) (2005), 43–92.Google Scholar
Lando, S. K. and Zvonkin, A. K., Graphs on Surfaces and Their Applications, Encyclopedia of Mathematical Sciences, 141 (Springer, Berlin–Heidelberg, 2004).Google Scholar
Mironov, A. D., Morozov, A. Y. and Natanzon, S. M., ‘Complete set of cut-and-join operators in the Hurwitz–Kontsevich theory’, Theoret. Math. Phys. 166(1) (2011), 1–22.Google Scholar
Mironov, A. D., Morozov, A. Y. and Natanzon, S. M., ‘Algebra of differential operators associated with Young diagrams’, J. Geom. Phys. 62(2) (2012), 148–155.Google Scholar
Simion, R., ‘Noncrossing partitions’, Discrete Math. 217(1–3) (2000), 367–409.Google Scholar
Sun, H., ‘A formula about W-operator and its application to Hurwitz number’, Discrete Math. 342(3) (2019), 715–722.Google Scholar