Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-21T18:38:28.904Z Has data issue: false hasContentIssue false
  • English
  • Français

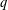DOUBLING TROPICAL $q$-DIFFERENCE ANALOGUE OF THE LEMMA ON THE LOGARITHMIC DERIVATIVE

Part of: Difference and functional equations Difference equations Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  12 September 2018

SI-QI CHENG Open the ORCID record for SI-QI CHENG [Opens in a new window]
SI-QI CHENG*
Affiliation:
Department of Mathematics, Taiyuan University of Technology, Shanxi 030024, China email chengsiqi0781@link.tyut.edu.cn, 1356992134@qq.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a tropical 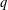$q$-difference analogue of the lemma on the logarithmic derivative for doubling tropical meromorphic functions.

Keywords

tropical q-difference meromorphic functionthe lemma on the logarithmic derivativedoubling property

MSC classification

Primary: 39A12: Discrete version of topics in analysis
Secondary: 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 474 - 480
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Barnett, D. C., Halburd, R. G., Morgan, W. and Korhonen, R. J., ‘Nevanlinna theory for the q-difference operator and meromorphic solutions of q-difference equations’, Proc. Roy. Soc. Edinburgh Sect. A 137(3) (2007), 457–474.Google Scholar
Halburd, R. G. and Southall, N. J., ‘Tropical Nevanlinna theory and ultradiscrete equations’, Int. Math. Res. Not. IMRN 39 (2009), 887–911.Google Scholar
Hayman, W. K., ‘On the characteristic of functions meromorphic in the plane and of their integrals’, Proc. Lond. Math. Soc. 14A (1965), 93–128.Google Scholar
Korhonen, R. J., Laine, I. and Tohge, K., Tropical Value Distribution Theory and Ultra-Discrete Equations (World Scientific, Singapore, 2015).Google Scholar
Laine, I., Liu, K. and Tohge, K., ‘Tropical variants of some complex analysis results’, Ann. Acad. Sci. Fenn. Math. Diss. 41 (2016), 923–946.Google Scholar
Laine, I. and Tohge, K., ‘Tropical Nevanlinna theory and second main theorem’, Proc. Lond. Math. Soc. 102(5) (2011), 883–922.Google Scholar
Tan, C. Q. and Li, J., ‘Some characterizations of upper doubling conditions on metric measure spaces’, Math. Nachr. 290 (2017), 142–158.Google Scholar
Tsai, Y.-L., ‘Working with tropical meromorphic functions of one variable’, Taiwanese J. Math. 16 (2012), 691–712.Google Scholar