Hostname: page-component-7479d7b7d-t6hkb Total loading time: 0 Render date: 2024-07-14T00:12:53.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and multiplicity results for quasilinear elliptic equations

Published online by Cambridge University Press:  17 April 2009

Wei Dong
Wei Dong
Affiliation:
Hebei University of Engineering, Handan, Hebei 056038, China and Department of Mathematics, School of Physical Sciences, University of Queensland, Brisbane Qld 4072, Australia, e-mail: wdong@maths.uq.edu.au
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The goal of this paper is to study the multiplicity of positive solutions of a class of quasilinear elliptic equations. Based on the mountain pass theorems and sub-and supersolutions argument for p-Laplacian operators, under suitable conditions on nonlinearity f(x, s), we show the follwing problem: 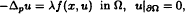, where Ω is a bounded open subset of RN, N ≥ 2, with smooth boundary, λ is a positive parameter and ∆p is the p-Laplacian operator with p > 1, possesses at least two positive solutions for large λ.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 71 , Issue 3 , June 2005 , pp. 377 - 386
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Azorero, J.P Garcia, Manfredi, J.J. and Alonso, I. Peral, Sobolev versus Hölder local minimisers and global multiplicity for some quasilinear elliptic equations, Comm.um Contemp. Math. 2 (2000), 385–404.CrossRefGoogle Scholar
[2]Diaz, J., Nonlinear partial differential equation and free boundary problems, Elliptic equations Vol. 1, Pitman Research Notes in Math. 106 (Pitman, Boston, M.A., 1985).Google Scholar
[3]Du, Y. and Guo, Z.M., ‘Liouville type results and eventual flatness of positive solutions for p-Laplacian equations’, Adv. Differential Equations 7 (2002), 1479–1512.CrossRefGoogle Scholar
[4]Du, Y. and Guo, Z.M., ‘Boundary blow-up solutions and their applications in quasilinear elliptic equations’, J. Analyse Math. 89 (2003), 277–302.CrossRefGoogle Scholar
[5]Dinca, G., Jebelean, P. and Mawhin, J., ‘A result of Ambrosetti-Rabinowitz type for p-Laplacian’, in Qualitative problems for differential equations and control theory (World Sci. Punlishing, Rever Edge, 1995), pp. 231–242.Google Scholar
[6]Guo, Z.M., ‘Some existence and multiplicity results for a class of quasilinear elliptic eigenvalue problem’, Nonlinear Anal. 18 (1992), 957–971.CrossRefGoogle Scholar
[7]Guo, D., Sun, J. and Qi, G., ‘Some extensions of the mountain pass lemma’, Diffential Integral Equations 1 (1988), 351–358.Google Scholar
[8]Rabinowitz, P.H., ‘Pairs of positive solutions of nonlinear elliptic partial differential equations’, Indiana Univ. Math. J. 23 (1973), 173–186.CrossRefGoogle Scholar
[9]Rabinowitz, P.H., Minimax methods in critical point theory with applications to differential equations, CBMS Regional Conf. Ser. in Math. 65 (Amer. Math. Soc., Province, R.I., 1986).CrossRefGoogle Scholar
[10]Takeuchi, S., ‘Positive solutions of a degenerate elliptic equation with logistic reaction’, Proc. Amer. Math. Soc. 129 (2000), 433–441.CrossRefGoogle Scholar
[11]Serrin, J. and Zou, H., ‘Cauchy-Liouville and universal boundedness theorems for quasilinear elliptic equations and inequalities’, Acta. Math. 189 (2002), 79–142.CrossRefGoogle Scholar
[12]Tolksdorf, P., ‘On the Dirichlet problem for quasilinear equations in domains with conial boundary points,’, Comm. Partial Differential Equations 8 (1983), 773–817.CrossRefGoogle Scholar
[13]Tolksdorf, P., ‘Regularity for more general class of quasilinear elliptic equations’, J. Differential Equations 51 (1984), 126–150.CrossRefGoogle Scholar
[14]Vazquez, J.L., ‘A strong maximum principle for some quasilinear elliptic equations’, Appl. Math. Optim. 12 (1984), 191–202.CrossRefGoogle Scholar