1. Introduction
In 1914, Ramanujan [Reference Ramanujan11] mysteriously stated some representations of
![]() $1/\pi $
, such as
$1/\pi $
, such as
 $$ \begin{align*} \sum_{k=0}^{\infty}(6k+1)\frac{(\frac{1}{2})_k^3}{k!^3 4^k} =\frac{4}{\pi}, \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{\infty}(6k+1)\frac{(\frac{1}{2})_k^3}{k!^3 4^k} =\frac{4}{\pi}, \end{align*} $$
where
![]() $(a)_n=a(a+1)\cdots (a+n-1)$
denotes the rising factorial. In 1997, Van Hamme [Reference Van Hamme13] conjectured 13 interesting p-adic analogues of Ramanujan-type formulas. For example,
$(a)_n=a(a+1)\cdots (a+n-1)$
denotes the rising factorial. In 1997, Van Hamme [Reference Van Hamme13] conjectured 13 interesting p-adic analogues of Ramanujan-type formulas. For example,
 $$ \begin{align} \sum_{k=0}^{(p-1)/2}(6k+1)\frac{(\frac{1}{2})_k^3}{k!^3 4^k} &\equiv p(-1)^{(p-1)/2}\pmod{p^4}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2}(6k+1)\frac{(\frac{1}{2})_k^3}{k!^3 4^k} &\equiv p(-1)^{(p-1)/2}\pmod{p^4}, \end{align} $$
where
![]() $p>3$
is a prime. Van Hamme himself gave proofs for three of them. Supercongruences of the form (1.1) are now called Ramanujan-type supercongruences (see [Reference Zudilin16]). The proof of (1.1) was first provided by Long [Reference Long9]. See [Reference Osburn and Zudilin10] for historical remarks on Van Hamme’s 13 supercongruences.
$p>3$
is a prime. Van Hamme himself gave proofs for three of them. Supercongruences of the form (1.1) are now called Ramanujan-type supercongruences (see [Reference Zudilin16]). The proof of (1.1) was first provided by Long [Reference Long9]. See [Reference Osburn and Zudilin10] for historical remarks on Van Hamme’s 13 supercongruences.
Recently, q-supercongruences have been investigated by several authors (see, for example, [Reference Guo and Schlosser3–Reference Liu and Petrov8, Reference Wang and Yue14, Reference Wei15]). In particular, in [Reference Guo and Schlosser3], the present authors proved that, for odd integers
![]() $d\geqslant 5$
,
$d\geqslant 5$
,
 $$ \begin{align} \sum_{k=0}^{n-1}[2dk+1]\frac{(q;q^d)_k^d}{(q^d;q^d)_k^d}q^{d(d-3)k/2} \equiv \begin{cases} 0\pmod{\Phi_n(q)^2} &\text{if } n\equiv -1\pmod{d},\\[2pt] 0\pmod{\Phi_n(q)^3} &\text{if } n\equiv -1/2\pmod{d}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{n-1}[2dk+1]\frac{(q;q^d)_k^d}{(q^d;q^d)_k^d}q^{d(d-3)k/2} \equiv \begin{cases} 0\pmod{\Phi_n(q)^2} &\text{if } n\equiv -1\pmod{d},\\[2pt] 0\pmod{\Phi_n(q)^3} &\text{if } n\equiv -1/2\pmod{d}. \end{cases} \end{align} $$
Here, we adopt the standard q-notation:
![]() $[n]=1+q+\cdots +q^{n-1}$
is the q-integer;
$[n]=1+q+\cdots +q^{n-1}$
is the q-integer;
![]() $(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
is the q-shifted factorial, with the abbreviated notation
$(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
is the q-shifted factorial, with the abbreviated notation
![]() $(a_1,a_2,\ldots ,a_m;q)_n=(a_1;q)_n (a_2;q)_n\cdots (a_m;q)_n$
, and
$(a_1,a_2,\ldots ,a_m;q)_n=(a_1;q)_n (a_2;q)_n\cdots (a_m;q)_n$
, and
![]() $\Phi _n(q)$
stands for the nth cyclotomic polynomial in q, which may be defined as
$\Phi _n(q)$
stands for the nth cyclotomic polynomial in q, which may be defined as
 $$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(k,n)=1}}(q-\zeta^k), \end{align*} $$
$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(k,n)=1}}(q-\zeta^k), \end{align*} $$
where
![]() $\zeta $
is a primitive nth root of unity.
$\zeta $
is a primitive nth root of unity.
It is worth mentioning that the q-congruence (1.2) is not true for
![]() $d=3$
. In [Reference Guo and Schlosser3], the present authors also gave the following companion of (1.2): for odd integers
$d=3$
. In [Reference Guo and Schlosser3], the present authors also gave the following companion of (1.2): for odd integers
![]() $d\geqslant 3$
and integers
$d\geqslant 3$
and integers
![]() $n>1$
,
$n>1$
,
 $$ \begin{align} \sum_{k=0}^{n-1}[2dk-1]\frac{(q^{-1};q^d)_k^d}{(q^d;q^d)_k^d} q^{d(d-1)k/2} \equiv \begin{cases} 0\pmod{\Phi_n(q)^2} &\text{if } n\equiv 1\pmod{d},\\[2pt] 0\pmod{\Phi_n(q)^3} &\text{if } n\equiv 1/2\pmod{d}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{n-1}[2dk-1]\frac{(q^{-1};q^d)_k^d}{(q^d;q^d)_k^d} q^{d(d-1)k/2} \equiv \begin{cases} 0\pmod{\Phi_n(q)^2} &\text{if } n\equiv 1\pmod{d},\\[2pt] 0\pmod{\Phi_n(q)^3} &\text{if } n\equiv 1/2\pmod{d}. \end{cases} \end{align} $$
In this paper, we prove the following q-supercongruence, which is a generalisation of the respective second cases of (1.2) and (1.3).
Theorem 1.1. Let d and r be odd integers satisfying
![]() $d\geqslant 3$
,
$d\geqslant 3$
,
![]() $r\leqslant d-4$
(in particular, r may be negative) and
$r\leqslant d-4$
(in particular, r may be negative) and
![]() $\gcd (d,r)=1$
. Let n be an integer such that
$\gcd (d,r)=1$
. Let n be an integer such that
![]() $n\geqslant (d-r)/2$
and
$n\geqslant (d-r)/2$
and
![]() $n\equiv -r/2\pmod {d}$
. Then
$n\equiv -r/2\pmod {d}$
. Then
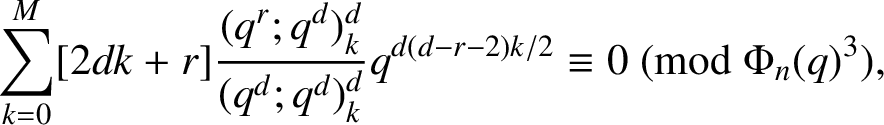 $$ \begin{align} \sum_{k=0}^{M}[2dk+r]\frac{(q^r;q^d)_k^d}{(q^d;q^d)_k^d}q^{d(d-r-2)k/2} \equiv 0 \pmod{\Phi_{n}(q)^3}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{M}[2dk+r]\frac{(q^r;q^d)_k^d}{(q^d;q^d)_k^d}q^{d(d-r-2)k/2} \equiv 0 \pmod{\Phi_{n}(q)^3}, \end{align} $$
where
![]() $M=(dn-2n-r)/d$
or
$M=(dn-2n-r)/d$
or
![]() $n-1$
.
$n-1$
.
Note that, in [Reference Guo and Schlosser5, Theorem 2], the present authors have already proved that (1.4) is true modulo
![]() $\Phi _n(q)^2$
and, further, conjectured that it is also true modulo
$\Phi _n(q)^2$
and, further, conjectured that it is also true modulo
![]() $\Phi _n(q)^4$
for
$\Phi _n(q)^4$
for
![]() $d\geqslant 5$
(see [Reference Guo and Schlosser5, Conjecture 3]). We believe that the full conjecture will be rather difficult to prove.
$d\geqslant 5$
(see [Reference Guo and Schlosser5, Conjecture 3]). We believe that the full conjecture will be rather difficult to prove.
We apply the method of creative microscoping, recently introduced in a paper by the first author with Zudilin [Reference Guo and Zudilin6], to prove Theorem 1.1. In our application of this method here, we suitably introduce the parameter a (such that the series satisfies the symmetry
![]() $a\leftrightarrow a^{-1}$
) into the terms of the series and prove that the congruence holds modulo
$a\leftrightarrow a^{-1}$
) into the terms of the series and prove that the congruence holds modulo
![]() $\Phi _n(q)$
, modulo
$\Phi _n(q)$
, modulo
![]() $1-aq^n$
and modulo
$1-aq^n$
and modulo
![]() $a-q^n$
. Thus, by the Chinese remainder theorem for coprime polynomials, the congruence holds modulo the product
$a-q^n$
. Thus, by the Chinese remainder theorem for coprime polynomials, the congruence holds modulo the product
![]() ${\Phi _n(q)(1-aq^n)(a-q^n)}$
. By letting
${\Phi _n(q)(1-aq^n)(a-q^n)}$
. By letting
![]() $a= 1$
, the congruence is established modulo
$a= 1$
, the congruence is established modulo
![]() $\Phi _n(q)^3$
.
$\Phi _n(q)^3$
.
Our paper is organised as follows. In Section 2, we list some tools that we require in our proof of Theorem 1.1. These consist of a lemma about an elementary q-congruence modulo a cyclotomic polynomial
![]() $\Phi _n(q)$
, and a very-well-poised Karlsson–Minton type summation by Gasper of which we need a special case. In Section 3, we first prove Theorem 3.1, which is a parametric generalisation of Theorem 1.1 that involves the insertion of different powers of the parameter a, appearing in geometric sequences, in the respective q-shifted factorials. Afterwards, we show how Theorem 1.1 follows from Theorem 3.1. We conclude with Section 4, where we elaborate on the merits and limits of the method of creative microscoping employed here in the quest of proving [Reference Guo and Schlosser5, Conjecture 3] (which remains open).
$\Phi _n(q)$
, and a very-well-poised Karlsson–Minton type summation by Gasper of which we need a special case. In Section 3, we first prove Theorem 3.1, which is a parametric generalisation of Theorem 1.1 that involves the insertion of different powers of the parameter a, appearing in geometric sequences, in the respective q-shifted factorials. Afterwards, we show how Theorem 1.1 follows from Theorem 3.1. We conclude with Section 4, where we elaborate on the merits and limits of the method of creative microscoping employed here in the quest of proving [Reference Guo and Schlosser5, Conjecture 3] (which remains open).
2. Preliminaries
We need the following result, which is due to the present authors [Reference Guo and Schlosser4, Lemma 2.1]. In order to make the paper self-contained, we include its short proof here.
Lemma 2.1. Let d, m and n be positive integers with
![]() $m\leqslant n-1$
. Let r be an integer satisfying
$m\leqslant n-1$
. Let r be an integer satisfying
![]() $dm\equiv -r\pmod {n}$
. Then, for
$dm\equiv -r\pmod {n}$
. Then, for
![]() $0\leqslant k\leqslant m$
and any indeterminate a,
$0\leqslant k\leqslant m$
and any indeterminate a,
 $$ \begin{align*} \frac{(aq^r;q^d)_{m-k}}{(q^d/a;q^d)_{m-k}} \equiv (-a)^{m-2k}\frac{(aq^r;q^d)_k}{(q^d/a;q^d)_k} q^{m(dm-d+2r)/2+(d-r)k} \pmod{\Phi_n(q)}. \end{align*} $$
$$ \begin{align*} \frac{(aq^r;q^d)_{m-k}}{(q^d/a;q^d)_{m-k}} \equiv (-a)^{m-2k}\frac{(aq^r;q^d)_k}{(q^d/a;q^d)_k} q^{m(dm-d+2r)/2+(d-r)k} \pmod{\Phi_n(q)}. \end{align*} $$
If
![]() $\gcd (d,n)=1$
, then the above q-congruence also holds for
$\gcd (d,n)=1$
, then the above q-congruence also holds for
![]() $a=1$
.
$a=1$
.
Proof. We first assume that a is an indeterminate. Since
![]() $q^{dm+r}\equiv q^n\equiv 1\pmod {\Phi _n(q)}$
,
$q^{dm+r}\equiv q^n\equiv 1\pmod {\Phi _n(q)}$
,
 $$ \begin{align} \frac{(aq^r;q^d)_{m} }{(q^d/a;q^d)_{m}} &=\frac{(1-aq^r)(1-aq^{d+r})\cdots (1-aq^{dm-d+r})} {(1-q^d/a)(1-q^{2d}/a)\cdots (1-q^{dm}/a)} \notag\\[5pt] &\equiv \frac{(1-aq^r)(1-aq^{d+r})\cdots (1-aq^{dm-d+r})} {(1-q^{d-dm-r}/a)(1-q^{2d-dm-r}/a)\cdots (1-q^{-r}/a)}\notag\\[5pt] &=(-a)^{m}q^{m(dm-d+2r)/2} \pmod{\Phi_n(q)}. \end{align} $$
$$ \begin{align} \frac{(aq^r;q^d)_{m} }{(q^d/a;q^d)_{m}} &=\frac{(1-aq^r)(1-aq^{d+r})\cdots (1-aq^{dm-d+r})} {(1-q^d/a)(1-q^{2d}/a)\cdots (1-q^{dm}/a)} \notag\\[5pt] &\equiv \frac{(1-aq^r)(1-aq^{d+r})\cdots (1-aq^{dm-d+r})} {(1-q^{d-dm-r}/a)(1-q^{2d-dm-r}/a)\cdots (1-q^{-r}/a)}\notag\\[5pt] &=(-a)^{m}q^{m(dm-d+2r)/2} \pmod{\Phi_n(q)}. \end{align} $$
Moreover, modulo
![]() $\Phi _n(q)$
,
$\Phi _n(q)$
,
 $$ \begin{align*} \frac{(aq^r;q^d)_{m-k}}{(q^d/a;q^d)_{m-k}} &=\frac{(aq^r;q^d)_{m}}{(q^d/a;q^d)_{m}} \frac{(1-q^{dm-dk+d}/a)(1-q^{dm-dk+2d}/a)\cdots (1-q^{dm}/a)} {(1-aq^{dm-dk+r})(1-aq^{dm-dk+d+r})\cdots (1-aq^{dm-d+r})} \\[5pt] &\equiv \frac{(aq^r;q^d)_{m}}{(q^d/a;q^d)_{m}} \frac{(1-q^{d-dk-r}/a)(1-q^{2d-dk-r}/a)\cdots (1-q^{-r}/a)} {(1-aq^{-dk})(1-aq^{d-dk})\cdots (1-aq^{-d})} \\[5pt] &=\frac{(aq^r;q^d)_{m}}{(q^d/a;q^d)_{m}} \frac{(aq^r;q^d)_k}{(q^d/a;q^d)_k} a^{-2k} q^{(d-r)k}. \end{align*} $$
$$ \begin{align*} \frac{(aq^r;q^d)_{m-k}}{(q^d/a;q^d)_{m-k}} &=\frac{(aq^r;q^d)_{m}}{(q^d/a;q^d)_{m}} \frac{(1-q^{dm-dk+d}/a)(1-q^{dm-dk+2d}/a)\cdots (1-q^{dm}/a)} {(1-aq^{dm-dk+r})(1-aq^{dm-dk+d+r})\cdots (1-aq^{dm-d+r})} \\[5pt] &\equiv \frac{(aq^r;q^d)_{m}}{(q^d/a;q^d)_{m}} \frac{(1-q^{d-dk-r}/a)(1-q^{2d-dk-r}/a)\cdots (1-q^{-r}/a)} {(1-aq^{-dk})(1-aq^{d-dk})\cdots (1-aq^{-d})} \\[5pt] &=\frac{(aq^r;q^d)_{m}}{(q^d/a;q^d)_{m}} \frac{(aq^r;q^d)_k}{(q^d/a;q^d)_k} a^{-2k} q^{(d-r)k}. \end{align*} $$
Substituting (2.1) into this q-congruence, we obtain the q-congruence in the lemma.
We now assume that
![]() $\gcd (d,n)=1$
and
$\gcd (d,n)=1$
and
![]() $a=1$
. Then the desired result follows from the same argument.
$a=1$
. Then the desired result follows from the same argument.
We will further utilise a very-well-poised Karlsson–Minton type summation due to Gasper [Reference Gasper, Ismail, Masson and Rahman1, Equation (5.13)] (see also [Reference Gasper and Rahman2, Example 2.33(i)]): that is,
 $$ \begin{align} &\sum_{k=0}^\infty\frac{(a,q\sqrt{a},-q\sqrt{a},b,a/b,d,e_1,aq^{n_1+1}/e_1,\dots, e_m,aq^{n_m+1}/e_m;q)_k}{(q,\sqrt{a},-\sqrt{a},aq/b,bq,aq/d,aq/e_1,e_1q^{-n_1}, \dots,aq/e_m,e_mq^{-n_m};q)_k}\bigg(\frac{q^{1-\nu}}d\bigg)^k\notag\\ &\quad=\frac{(q,aq,aq/bd,bq/d;q)_\infty}{(bq,aq/b,aq/d,q/d;q)_\infty} \prod_{j=1}^m\frac{(aq/be_j,bq/e_j;q)_{n_j}}{(aq/e_j,q/e_j;q)_{n_j}}, \end{align} $$
$$ \begin{align} &\sum_{k=0}^\infty\frac{(a,q\sqrt{a},-q\sqrt{a},b,a/b,d,e_1,aq^{n_1+1}/e_1,\dots, e_m,aq^{n_m+1}/e_m;q)_k}{(q,\sqrt{a},-\sqrt{a},aq/b,bq,aq/d,aq/e_1,e_1q^{-n_1}, \dots,aq/e_m,e_mq^{-n_m};q)_k}\bigg(\frac{q^{1-\nu}}d\bigg)^k\notag\\ &\quad=\frac{(q,aq,aq/bd,bq/d;q)_\infty}{(bq,aq/b,aq/d,q/d;q)_\infty} \prod_{j=1}^m\frac{(aq/be_j,bq/e_j;q)_{n_j}}{(aq/e_j,q/e_j;q)_{n_j}}, \end{align} $$
where
![]() $n_1,\dots ,n_m$
are nonnegative integers,
$n_1,\dots ,n_m$
are nonnegative integers,
![]() $\nu =n_1+\cdots +n_m$
and the convergence condition
$\nu =n_1+\cdots +n_m$
and the convergence condition
![]() $|q^{1-\nu }/d|<1$
is needed when the series does not terminate. We point out that an elliptic extension of the terminating
$|q^{1-\nu }/d|<1$
is needed when the series does not terminate. We point out that an elliptic extension of the terminating
![]() $d=q^{-\nu }$
case of (2.2) was given by Rosengren and the second author in [Reference Rosengren and Schlosser12, Equation (1.7)].
$d=q^{-\nu }$
case of (2.2) was given by Rosengren and the second author in [Reference Rosengren and Schlosser12, Equation (1.7)].
In particular, we notice that the right-hand side of (2.2) vanishes for
![]() $d=bq$
. Further, taking
$d=bq$
. Further, taking
![]() $b=q^{-N}$
, we get the summation formula
$b=q^{-N}$
, we get the summation formula
 $$ \begin{align} \sum_{k=0}^N\frac{(a,q\sqrt{a},-q\sqrt{a},e_1,aq^{n_1+1}/e_1,\dots, e_m,aq^{n_m+1}/e_m,q^{-N};q)_k}{(q,\sqrt{a},-\sqrt{a},aq/e_1,e_1q^{-n_1}, \dots,aq/e_m,e_mq^{-n_m},aq^{N+1};q)_k}q^{(N-\nu)k}=0, \end{align} $$
$$ \begin{align} \sum_{k=0}^N\frac{(a,q\sqrt{a},-q\sqrt{a},e_1,aq^{n_1+1}/e_1,\dots, e_m,aq^{n_m+1}/e_m,q^{-N};q)_k}{(q,\sqrt{a},-\sqrt{a},aq/e_1,e_1q^{-n_1}, \dots,aq/e_m,e_mq^{-n_m},aq^{N+1};q)_k}q^{(N-\nu)k}=0, \end{align} $$
provided that
![]() $N>\nu =n_1+\cdots +n_m$
.
$N>\nu =n_1+\cdots +n_m$
.
3. A parametric generalisation and proof of Theorem 1.1
We now give a parametric generalisation of Theorem 1.1.
Theorem 3.1. Let d and r be odd integers satisfying
![]() $d\geqslant 3$
,
$d\geqslant 3$
,
![]() $r\leqslant d-4$
(in particular, r may be negative) and
$r\leqslant d-4$
(in particular, r may be negative) and
![]() $\gcd (d,r)=1$
. Let n be an integer such that
$\gcd (d,r)=1$
. Let n be an integer such that
![]() $n\geqslant (d-r)/2$
and
$n\geqslant (d-r)/2$
and
![]() $n\equiv -r/2\pmod {d}$
. Then, modulo
$n\equiv -r/2\pmod {d}$
. Then, modulo
![]() $\Phi _n(q)(1-aq^n)(a-q^n)$
,
$\Phi _n(q)(1-aq^n)(a-q^n)$
,
 $$ \begin{align} \sum_{k=0}^{M}&[2dk+r]\frac{(a^{d-2}q^r, a^{d-4}q^r,\ldots, aq^r;q^d)_k} {(a^{d-2}q^d, a^{d-4}q^d,\ldots,aq^d;q^d)_k}\notag\\ &\times \frac{(a^{2-d}q^r, a^{4-d}q^r,\ldots, a^{-1}q^r;q^d)_k (q^r;q^d)_k} {(a^{2-d}q^d, a^{4-d}q^d,\ldots, a^{-1}q^d;q^d)_k (q^d;q^d)_k } q^{d(d-r-2)k/2} \equiv 0, \end{align} $$
$$ \begin{align} \sum_{k=0}^{M}&[2dk+r]\frac{(a^{d-2}q^r, a^{d-4}q^r,\ldots, aq^r;q^d)_k} {(a^{d-2}q^d, a^{d-4}q^d,\ldots,aq^d;q^d)_k}\notag\\ &\times \frac{(a^{2-d}q^r, a^{4-d}q^r,\ldots, a^{-1}q^r;q^d)_k (q^r;q^d)_k} {(a^{2-d}q^d, a^{4-d}q^d,\ldots, a^{-1}q^d;q^d)_k (q^d;q^d)_k } q^{d(d-r-2)k/2} \equiv 0, \end{align} $$
where
![]() $(dn-2n-r)/d\leqslant M\leqslant n-1$
.
$(dn-2n-r)/d\leqslant M\leqslant n-1$
.
Proof. It is easy to see that
![]() $\gcd (d,n)=1$
and, thereby, none of the numbers
$\gcd (d,n)=1$
and, thereby, none of the numbers
![]() $d,2d,\ldots , (n-1)d$
are multiples of n. This means that the denominators of the left-hand side of (3.1) contain neither the factor
$d,2d,\ldots , (n-1)d$
are multiples of n. This means that the denominators of the left-hand side of (3.1) contain neither the factor
![]() $1-aq^n$
nor
$1-aq^n$
nor
![]() $1-a^{-1}q^n$
. Thus, for
$1-a^{-1}q^n$
. Thus, for
![]() $a=q^{-n}$
or
$a=q^{-n}$
or
![]() $a=q^n$
, the left-hand side of (3.1) can be written as
$a=q^n$
, the left-hand side of (3.1) can be written as
 $$ \begin{align} &\sum_{k=0}^{(dn-2n-r)/d}[2dk+r]\frac{(q^{r-(d-2)n}, q^{r-(d-4)n},\ldots, q^{r-n};q^d)_k } {(q^{d-(d-2)n}, q^{d-(d-4)n},\ldots, q^{d-n};q^d)_k } \notag\\ &\qquad\quad\times \frac{(q^{(d-2)n+r}, q^{(d-4)n+r},\ldots,q^{n+r};q^d)_k (q^r;q^d)_k} {(q^{(d-2)n+d}, q^{(d-4)n+d},\ldots, q^{n+d};q^d)_k (q^d;q^d)_k } q^{d(d-r-2)k/2}, \end{align} $$
$$ \begin{align} &\sum_{k=0}^{(dn-2n-r)/d}[2dk+r]\frac{(q^{r-(d-2)n}, q^{r-(d-4)n},\ldots, q^{r-n};q^d)_k } {(q^{d-(d-2)n}, q^{d-(d-4)n},\ldots, q^{d-n};q^d)_k } \notag\\ &\qquad\quad\times \frac{(q^{(d-2)n+r}, q^{(d-4)n+r},\ldots,q^{n+r};q^d)_k (q^r;q^d)_k} {(q^{(d-2)n+d}, q^{(d-4)n+d},\ldots, q^{n+d};q^d)_k (q^d;q^d)_k } q^{d(d-r-2)k/2}, \end{align} $$
where we have used
![]() $(q^{r-(d-2)n};q^d)_k=0$
for
$(q^{r-(d-2)n};q^d)_k=0$
for
![]() $k>(dn-2n-r)/d$
. Specialising the parameters in (2.3) by
$k>(dn-2n-r)/d$
. Specialising the parameters in (2.3) by
![]() $N=(dn-2n-r)/d$
,
$N=(dn-2n-r)/d$
,
![]() $a=q^r$
,
$a=q^r$
,
![]() $q\mapsto q^d$
,
$q\mapsto q^d$
,
![]() $m=(d-1)/2$
,
$m=(d-1)/2$
,
![]() $e_i=q^{r-(d-2i-2)n}$
(
$e_i=q^{r-(d-2i-2)n}$
(
![]() $1\leqslant i\leqslant m-1$
),
$1\leqslant i\leqslant m-1$
),
![]() $e_m=q^{(d+r)/2}$
,
$e_m=q^{(d+r)/2}$
,
![]() $n_1=\cdots =n_{m-1}=(2n+r-d)/d$
and
$n_1=\cdots =n_{m-1}=(2n+r-d)/d$
and
![]() $n_m=(2n+r-d)/(2d)$
and noticing
$n_m=(2n+r-d)/(2d)$
and noticing
![]() $N-(n_1+\cdots +n_m)=(d-r-2)/2>0$
, we see that (3.2) is equal to
$N-(n_1+\cdots +n_m)=(d-r-2)/2>0$
, we see that (3.2) is equal to
![]() $0$
. This proves that (3.1) holds modulo
$0$
. This proves that (3.1) holds modulo
![]() $(1-aq^n)(a-q^n)$
.
$(1-aq^n)(a-q^n)$
.
For
![]() $M=(dn-2n-r)/d$
, by Lemma 2.1, we can easily check that
$M=(dn-2n-r)/d$
, by Lemma 2.1, we can easily check that
 $$ \begin{align*} &[2d(M-k)+r]\frac{(a^{d-2}q^r, a^{d-4}q^r,\ldots, aq^r;q^d)_{M-k}} {(a^{d-2}q^d, a^{d-4}q^d,\ldots,aq^d;q^d)_{M-k}}\notag\\ &\qquad \times \frac{(a^{2-d}q^r, a^{4-d}q^r,\ldots, a^{-1}q^r;q^d)_{M-k} (q^r;q^d)_{M-k}} {(a^{2-d}q^d, a^{4-d}q^d,\ldots, a^{-1}q^d;q^d)_{M-k} (q^d;q^d)_{M-k} } q^{d(d-r-2)(M-k)/2} \\ &\quad\equiv -[2dk+r]\frac{(a^{d-2}q^r, a^{d-4}q^r,\ldots, aq^r;q^d)_k} {(a^{d-2}q^d, a^{d-4}q^d,\ldots,aq^d;q^d)_k}\notag\\ &\qquad\times \frac{(a^{2-d}q^r, a^{4-d}q^r,\ldots, a^{-1}q^r;q^d)_k (q^r;q^d)_k} {(a^{2-d}q^d, a^{4-d}q^d,\ldots, a^{-1}q^d;q^d)_k (q^d;q^d)_k } q^{d(d-r-2)k/2} \pmod{\Phi_n(q)}. \end{align*} $$
$$ \begin{align*} &[2d(M-k)+r]\frac{(a^{d-2}q^r, a^{d-4}q^r,\ldots, aq^r;q^d)_{M-k}} {(a^{d-2}q^d, a^{d-4}q^d,\ldots,aq^d;q^d)_{M-k}}\notag\\ &\qquad \times \frac{(a^{2-d}q^r, a^{4-d}q^r,\ldots, a^{-1}q^r;q^d)_{M-k} (q^r;q^d)_{M-k}} {(a^{2-d}q^d, a^{4-d}q^d,\ldots, a^{-1}q^d;q^d)_{M-k} (q^d;q^d)_{M-k} } q^{d(d-r-2)(M-k)/2} \\ &\quad\equiv -[2dk+r]\frac{(a^{d-2}q^r, a^{d-4}q^r,\ldots, aq^r;q^d)_k} {(a^{d-2}q^d, a^{d-4}q^d,\ldots,aq^d;q^d)_k}\notag\\ &\qquad\times \frac{(a^{2-d}q^r, a^{4-d}q^r,\ldots, a^{-1}q^r;q^d)_k (q^r;q^d)_k} {(a^{2-d}q^d, a^{4-d}q^d,\ldots, a^{-1}q^d;q^d)_k (q^d;q^d)_k } q^{d(d-r-2)k/2} \pmod{\Phi_n(q)}. \end{align*} $$
It now becomes evident that the kth and
![]() $(M-k)$
th summands on the left-hand side of (3.1) cancel each other modulo
$(M-k)$
th summands on the left-hand side of (3.1) cancel each other modulo
![]() $\Phi _n(q)$
. Therefore, the left-hand side of (3.1) is congruent to
$\Phi _n(q)$
. Therefore, the left-hand side of (3.1) is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)$
for
$\Phi _n(q)$
for
![]() $M=(dn-2n-r)/d$
. Furthermore, for any k in the range
$M=(dn-2n-r)/d$
. Furthermore, for any k in the range
![]() $(dn-2n-r)/d<k\leqslant n-1$
, we have
$(dn-2n-r)/d<k\leqslant n-1$
, we have
![]() $(q^r;q^d)_k/(q^d;q^d)_k\equiv 0\pmod {\Phi _n(q)}$
. Hence, the q-congruence (3.1) also holds modulo
$(q^r;q^d)_k/(q^d;q^d)_k\equiv 0\pmod {\Phi _n(q)}$
. Hence, the q-congruence (3.1) also holds modulo
![]() $\Phi _n(q)$
for
$\Phi _n(q)$
for
![]() $(dn-2n-r)/d<M\leqslant n-1$
.
$(dn-2n-r)/d<M\leqslant n-1$
.
Proof of Theorem 1.1
Since
![]() $\gcd (n,d)=1$
and
$\gcd (n,d)=1$
and
![]() $0\leqslant k\leqslant n-1$
, the factors related to a in the denominators of the left-hand side of (3.1) are relatively prime to
$0\leqslant k\leqslant n-1$
, the factors related to a in the denominators of the left-hand side of (3.1) are relatively prime to
![]() $\Phi _n(q)$
when
$\Phi _n(q)$
when
![]() $a=1$
. On the other hand, the polynomial
$a=1$
. On the other hand, the polynomial
![]() $(1-aq^n)(a-q^n)$
has the factor
$(1-aq^n)(a-q^n)$
has the factor
![]() $\Phi _n(q)^2$
when
$\Phi _n(q)^2$
when
![]() $a=1$
. Thus, letting
$a=1$
. Thus, letting
![]() $a=1$
in (3.1), we see that (1.4) holds modulo
$a=1$
in (3.1), we see that (1.4) holds modulo
![]() $\Phi _n(q)^3$
.
$\Phi _n(q)^3$
.
4. Concluding remarks
We have inserted different powers of the parameter a, appearing in geometric sequences, in the respective q-shifted factorials on the left-hand side of (1.4), in order to establish the desired generalised congruence modulo
![]() $(1-aq^n)(a-q^n)$
. The proof of Theorem 1.1 is similar to the proofs in [Reference Guo and Schlosser3] but is quite different from those in [Reference Guo and Zudilin6], where the parameter a is inserted in a more standard way (without higher powers of a).
$(1-aq^n)(a-q^n)$
. The proof of Theorem 1.1 is similar to the proofs in [Reference Guo and Schlosser3] but is quite different from those in [Reference Guo and Zudilin6], where the parameter a is inserted in a more standard way (without higher powers of a).
While the method of creative microscoping enabled us to strengthen [Reference Guo and Schlosser5, Theorem 2] to the congruence modulo
![]() $\Phi _n(q)^3$
in Theorem 1.1, we believe that it is rather unlikely that the validity of (1.4) modulo
$\Phi _n(q)^3$
in Theorem 1.1, we believe that it is rather unlikely that the validity of (1.4) modulo
![]() $\Phi _n(q)^4$
for
$\Phi _n(q)^4$
for
![]() $d\geqslant 5$
[Reference Guo and Schlosser5, Conjecture 3] can be proved by the method of creative microscoping, since the parametric generalisation in (3.1) does not hold modulo
$d\geqslant 5$
[Reference Guo and Schlosser5, Conjecture 3] can be proved by the method of creative microscoping, since the parametric generalisation in (3.1) does not hold modulo
![]() $\Phi _n(q)^2(1-aq^n)(a-q^n)$
, in general. For this reason, the proof of (1.4) modulo
$\Phi _n(q)^2(1-aq^n)(a-q^n)$
, in general. For this reason, the proof of (1.4) modulo
![]() $\Phi _n(q)^2$
given in [Reference Guo and Schlosser5] still has its virtue. Recall that the present authors, in [Reference Guo and Schlosser5], wrote the left-hand side of (1.4) as a product of two rational functions X and Y, and showed that X is congruent to
$\Phi _n(q)^2$
given in [Reference Guo and Schlosser5] still has its virtue. Recall that the present authors, in [Reference Guo and Schlosser5], wrote the left-hand side of (1.4) as a product of two rational functions X and Y, and showed that X is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)^2$
. Hence, to prove [Reference Guo and Schlosser5, Conjecture 3], it remains to prove that Y is also congruent to
$\Phi _n(q)^2$
. Hence, to prove [Reference Guo and Schlosser5, Conjecture 3], it remains to prove that Y is also congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)^2$
. We hope that an interested reader can shed light on this problem and settle the conjecture.
$\Phi _n(q)^2$
. We hope that an interested reader can shed light on this problem and settle the conjecture.