Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T07:06:07.904Z Has data issue: false hasContentIssue false
  • English
  • Français

FORMAL GROUPS AND INVARIANT DIFFERENTIALS OF ELLIPTIC CURVES

Part of: Curves

Published online by Cambridge University Press:  04 May 2015

MOHAMMAD SADEK
MOHAMMAD SADEK*
Affiliation:
Department of Mathematics and Actuarial Science, American University in Cairo, Egypt email mmsadek@aucegypt.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we find a power series expansion of the invariant differential 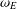${\it\omega}_{E}$ of an elliptic curve 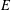$E$ defined over 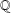$\mathbb{Q}$, where 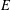$E$ is described by certain families of Weierstrass equations. In addition, we derive several congruence relations satisfied by the trace of the Frobenius endomorphism of 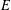$E$.

Keywords

elliptic curvesformal groupsinvariant differentials

MSC classification

Primary: 14H52: Elliptic curves
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 44 - 51
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bluher, A., ‘A leisurely introduction to formal groups and elliptic curves’, 1997, available on-line at http://www.math.uiuc.edu/Algebraic-Number-Theory/0076/.Google Scholar
Coster, M., ‘Generalisation of a congruence of Gauss’, J. Number Theory 29(3) (1988), 300–310.CrossRefGoogle Scholar
Coster, M. J. and Van Hamme, L., ‘Supercongruences of Atkin and Swinnerton-Dyer type for Legendre polynomials’, J. Number Theory 38 (1991), 265–286.CrossRefGoogle Scholar
Hazewinkel, M., ‘Three lectures on formal groups’, Canad. Math. Soc. Conf. Proc. 5 (1986), 51–67.Google Scholar
Honda, T., ‘Formal groups and zeta-functions’, Osaka J. Math. 5(2) (1968), 199–213.Google Scholar
Kubert, D. S., ‘Universal bounds on the torsion of elliptic curves’, Proc. Lond. Math. Soc. (3) 33(2) (1976), 193–237.CrossRefGoogle Scholar
Silverman, J., The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 106 (Springer, New York, 1986).CrossRefGoogle Scholar
Stienstra, J., ‘Formal groups and congruences for L-functions’, Amer. J. Math. 109(6) (1987), 1111–1127.CrossRefGoogle Scholar
Stienstra, J. and Beukers, F., ‘On the Picard–Fuchs equation and the formal Brauer group of certain elliptic K3-surfaces’, Math. Ann. 271 (1985), 269–304.CrossRefGoogle Scholar
Wolfram Research, Mathematica, ver. 5.0.Google Scholar
Yasuda, S., ‘Explicit t-expansions for the elliptic curve E : y 2 = 4(x 3 + Ax + B)’, Proc. Japan Acad. Ser. A Math. Sci. 89(9) (2013), 123–127.CrossRefGoogle Scholar