Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frappier, Clément
2001.
A Unified Calculus Using the Generalized Bernoulli Polynomials.
Journal of Approximation Theory,
Vol. 109,
Issue. 2,
p.
279.
Frappier, Clément
2005.
New results of α-calculus.
Integral Transforms and Special Functions,
Vol. 16,
Issue. 3,
p.
199.
Costabile, F.
and
Napoli, A.
2009.
A special class of polynomials related to non-classic general interpolatory problems.
Integral Transforms and Special Functions,
Vol. 20,
Issue. 7,
p.
539.
Costabile, F.
and
Napoli, A.
2010.
Special even polynomials and related interpolatory problems.
Integral Transforms and Special Functions,
Vol. 21,
Issue. 3,
p.
183.
Eweis, S. Z. H.
and
Mansour, Z. S. I.
2022.
Generalized q-Bernoulli Polynomials Generated by Jackson q-Bessel Functions.
Results in Mathematics,
Vol. 77,
Issue. 3,
Kuş, Semra
and
Tuglu, Naim
2025.
Orthogonalizing q-Bernoulli polynomials.
Demonstratio Mathematica,
Vol. 58,
Issue. 1,

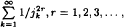 , where
, where 