Hostname: page-component-7bb8b95d7b-fmk2r Total loading time: 0 Render date: 2024-09-12T22:21:31.892Z Has data issue: false hasContentIssue false
  • English
  • Français

A Hilbert algebra of Hilbert-Schmidt quadratic operators

Published online by Cambridge University Press:  17 April 2009

J.C. Amson  and
N. Gopal Reddy
J.C. Amson
Affiliation:
Department of Mathematical Sciences, The Mathematical Institute, University of St Andrews, St Andrews Fife Ky16 9SS, Scotland, United Kingdom
N. Gopal Reddy
Affiliation:
Department of Mathematics, Osmania University, H No 9–29 Ravindar Nagar Colony, Habisguda, Hyderabad 500 007, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A quadratic operator Q of Hilbert-Schmidt class on a real separable Hilbert space H is shown to be uniquely representable as a sequence 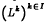of self-adjoint linear operators of Hilbert-Schmidt class on H, such that Q(x) = Σk〈Lkx, x〉uk with respect to a Hilbert basis 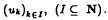. It is shown that with the norm | ‖Q‖ | = (Σk ‖Lk‖2)½ and inner-product 〈〈〈Q, P〉〉〉 = Σk 〈〈Lk, Mk〉〉, together with a multiplication defined componentwise through the composition of the linear components, the vector space of all Hilbert-Schmidt quadratic operators Q on H becomes a linear H*-algebra containing an ideal of nuclear (trace class) quadratic operators. In the finite dimensional case, each Q is also shown to have another representation as a block-diagonal matrix of Hilbert-Schmidt class which simplifies the practical computation and manipulation of quadratic operators.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 41 , Issue 1 , February 1990 , pp. 123 - 134
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Ambrose, W., ‘Structure theorems for a special class of Banach Algebras’, Trans. Amer. Math. Soc 57 (1945), 364–386.CrossRefGoogle Scholar
[2]Amson, J.C., ‘Multimatrix polynomial representations of the polar composition of polynomial operations’, Proc. London Math. Soc. (3) XXV (1972), 465–485.CrossRefGoogle Scholar
[3]Amson, J.C., ‘Representations of multilinear and polynomial operations on vector spaces’, J. London Math Soc. (2) 4 (1972), 394–400.CrossRefGoogle Scholar
[4]Bochnak, J. and Siciak, J., ‘Polynomials and multilinear mappings in topological vector spaces’, Studia Math. 39 (1971), 59–76.CrossRefGoogle Scholar
[5]Dunford, N. and Schwartz, J.T., Linear Operators, Part II: Spectral Theory (Interscience, London, 1963).Google Scholar
[6]Gel'fand, I.M. and Vilenkin, N. Ya., Generalized functions, volume 4, Applications of harmonic analysis (Academic Press, London, 1964). (Translated from the Russian edition 1961).Google Scholar
[7]Greub, W.H., Multilinear Algebra (Springer-Verlag, Berlin, Heidelberg, New York, 1967). (2nd Edition 1978).Google Scholar
[8]Prenter, P.M., ‘On polynomial operators and equations’, in Nonlinear functional analysis and applications, (Mathematics Center, University of Wisconsin, Madison) Editor Rall, L.B. (Academic Press, London, 1971).Google Scholar
[9]Schatten, R., Norm ideals of completely continuous operators: Erg. d. Math. 27 (Springer-Verlag, Berlin, Heidelberg, New York (2nd printing), 1970).CrossRefGoogle Scholar
[10]Weidman, J., Linear operators in Hilbert space (Springer-Verlag, Berlin, Heidelberg, New York, 1980).Google Scholar