Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Anh, V.V.
1989.
Starlike functions with a fixed coefficient.
Bulletin of the Australian Mathematical Society,
Vol. 39,
Issue. 1,
p.
145.
Patel, J.
and
Sahoo, P.
2003.
Properties of a class of multivalent analytic functions.
Computers & Mathematics with Applications,
Vol. 46,
Issue. 10-11,
p.
1633.
Aghalary, Rasoul
2008.
Some properties of a Certain family of Meromorphically Univalent Functions defined by an Integral Operator.
Kyungpook mathematical journal,
Vol. 48,
Issue. 3,
p.
379.
ALI, MD FIROZ
and
VASUDEVARAO, A.
2015.
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS.
Journal of the Australian Mathematical Society,
Vol. 99,
Issue. 3,
p.
315.
Niu, Xiaomeng
Tang, Huo
and
Ma, Lina
2020.
The logarithmic coefficients and the successive coefficients of Bazilevič functions of order α + iμ.
Complex Variables and Elliptic Equations,
Vol. 65,
Issue. 11,
p.
1962.
Srivastava, H. M.
Prajapati, A.
and
Gochhayat, P.
2022.
Integral means and Yamashita’s conjecture associated with the Janowski type (j, k)-symmetric starlike functions.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 4,

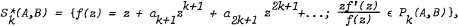
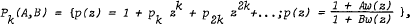
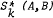 are also derived.
are also derived.