Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-29T22:48:16.890Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL-GLOBAL PRINCIPLE FOR THE FINITENESS AND ARTINIANNESS OF GENERALISED LOCAL COHOMOLOGY MODULES

Part of: Commutative algebra: Homological methods Chain conditions, finiteness conditions

Published online by Cambridge University Press:  20 August 2012

ALI FATHI
ALI FATHI*
Affiliation:
Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran (email: alif1387@gmail.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

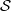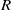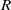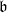Let $\mathcal S$ be a Serre subcategory of the category of $R$-modules, where $R$ is a commutative Noetherian ring. Let $\mathfrak a$ and $\mathfrak b$ be ideals of 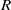$R$ and let 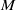$M$ and 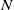$N$ be finite 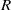$R$-modules. We prove that if 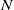$N$ and 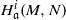$H^i_{\mathfrak a}(M,N)$ belong to 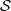$\mathcal S$ for all 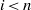$i\lt n$ and if 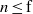$n\leq \mathrm {f}$-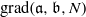$\mathrm {grad}({\mathfrak a},{\mathfrak b},N )$, then 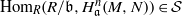$\mathrm {Hom}_{R}(R/{\mathfrak b},H^n_{{\mathfrak a}}(M,N))\in \mathcal S$. We deduce that if either 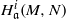$H^i_{\mathfrak a}(M,N)$ is finite or 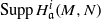$\mathrm {Supp}\,H^i_{\mathfrak a}(M,N)$ is finite for all 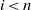$i\lt n$, then 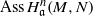$\mathrm {Ass}\,H^n_{\mathfrak a}(M,N)$ is finite. Next we give an affirmative answer, in certain cases, to the following question. 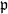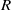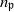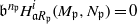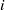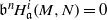If, for each prime ideal ${\mathfrak {p}}$ of $R$, there exists an integer $n_{\mathfrak {p}}$ such that $\mathfrak b^{n_{\mathfrak {p}}} H^i_{\mathfrak a R_{\mathfrak {p}}}({M_{\mathfrak {p}}},{N_{\mathfrak {p}}})=0$ for every $i$ less than a fixed integer $t$, then does there exist an integer $n$ such that $\mathfrak b^nH^i_{\mathfrak a}(M,N)=0$ for all 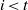$i\lt t$? A formulation of this question is referred to as the local-global principle for the annihilation of generalised local cohomology modules. Finally, we prove that there are local-global principles for the finiteness and Artinianness of generalised local cohomology modules.

Keywords

(generalised) local cohomology modulefinitenessArtiniannesslocal-global principlefilter regular sequence

MSC classification

Secondary: 13D45: Local cohomology 13E10: Artinian rings and modules, finite-dimensional algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 3 , June 2013 , pp. 480 - 492
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Bijan-Zadeh, M. H., ‘A common generalization of local cohomology theories’, Glasg. Math. J. 21(2) (1980), 173–181.CrossRefGoogle Scholar
[2]Bruns, W. & Herzog, J., Cohen–Macaulay Rings (Cambridge University Press, Cambridge, 1993).Google Scholar
[3]Brodmann, M. P., Rotthaus, C. & Sharp, R. Y., ‘On annihilators and associated primes of local cohomology modules’, J. Pure Appl. Algebra 153 (2000), 197–227.CrossRefGoogle Scholar
[4]Brodmann, M. P. & Sharp, R. Y., Local Cohomology: An Algebraic Introduction with Geometric Applications (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
[5]Chu, L., ‘Cofiniteness and finiteness of generalized local cohomology modules’, Bull. Aust. Math. Soc. 80(2) (2009), 244–250.CrossRefGoogle Scholar
[6]Faltings, G., ‘Über die Annulatoren lokaler Kohomologiegruppen’, Arch. Math. 30 (1978), 473–476.CrossRefGoogle Scholar
[7]Faltings, G., ‘Der Endlichkeitssatz in der lokalen Kohomologie’, Math. Ann. 255 (1981), 45–56.CrossRefGoogle Scholar
[8]Fathi, A., Tehranian, A. & Zakeri, H., ‘Filter regular sequences and generalized local cohomology modules’, arXiv:1207.1296v1.Google Scholar
[9]Herzog, J., ‘Komplexe Auflösungen und Dualität in der lokalen Algebra’, Habilitationsschrift, Universität Regensburg, 1970.Google Scholar
[10]Katzman, M., ‘An example of an infinite set of associated primes of a local cohomology module’, J. Algebra (1) 252 (2002), 161–166.CrossRefGoogle Scholar
[11]Lü, R. & Tang, Z., ‘The $f$-depth of an ideal on a module’, Proc. Amer. Math. Soc. 130(7) (2002), 1905–1912.CrossRefGoogle Scholar
[12]Nagel, N. & Schenzel, P., ‘Cohomological annihilators and Castelnovo–Mamford regularity’, in: Commutative Algebra: Syzygies, Multiplicities, and Bi-rational Algebra (South Hadley, MA, 1992) (American Mathematical Society, Providence, RI, 1994), pp. 307–328.CrossRefGoogle Scholar
[13]Quy, P. H., ‘On the finiteness of associated primes of local cohomology modules’, Proc. Amer. Math. Soc. 138(6) (2010), 1965–1968.CrossRefGoogle Scholar
[14]Raghavan, K. N., ‘Local-global principle for annihilation of local cohomology’, Contemp. Math. 159 (1994), 329–331.CrossRefGoogle Scholar
[15]Schenzel, P., Trung, N. V. & Cuong, N. T., ‘Verallgemeinerte Cohen–Macaulay-Moduln’, Math. Nachr. 85 (1978), 57–73.CrossRefGoogle Scholar
[16]Singh, A., ‘$p$-torsion elements in local cohomology modules’, Math. Res. Lett. 7(2–3) (2000), 165–176.CrossRefGoogle Scholar
[17]Stückrad, J. & Vogel, W., Buchsbaum Rings and Applications (VEB Deutscher Verlag der Wissenschaften, Berlin, 1986).CrossRefGoogle Scholar
[18]Suzuki, N., ‘On the generalized local cohomology and its duality’, J. Math. Kyoto Univ. 18 (1978), 71–85.Google Scholar
[19]Tajarod, R. & Zakeri, H., ‘On the local-global principle and the finiteness of associated primes of local cohomology modules’, Math. J. Toyama Univ. 23 (2000), 29–40.Google Scholar
[20]Tang, Z., ‘Local-global principle for the Artinianness of local cohomology modules’, Comm. Algebra 40(1) (2012), 58–63.CrossRefGoogle Scholar
[21]Trung, N. V., ‘Absolutely superficial sequences’, Math. Proc. Cambridge Philos. Soc. 93 (1983), 35–47.CrossRefGoogle Scholar
[22]Vasconcelos, W. V., Divisor Theory in Module Categories (North-Holland, Amsterdam, 1974).Google Scholar
[23]Yassemi, S., Khatami, L. & Sharif, T., ‘Associated primes of generalized local cohomology modules’, Comm. Algebra 30(1) (2002), 327–330.CrossRefGoogle Scholar